神经网络入门篇：激活函数的导数（Derivatives of activation functions）

激活函数的导数

在神经网络中使用反向传播的时候，真的需要计算激活函数的斜率或者导数。针对以下四种激活，求其导数如下：

1）sigmoid activation function

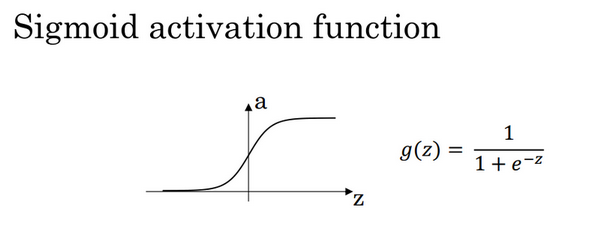
图1.8.1

其具体的求导如下：

公式3.25：

\(\frac{d}{dz}g(z) = {\frac{1}{1 + e^{-z}} (1-\frac{1}{1 + e^{-z}})}=g(z)(1-g(z))\)

注：

当\(z\) = 10或\(z= -10\) ; \(\frac{d}{dz}g(z)\approx0\)

当$z $= 0 , \(\frac{d}{dz}g(z)\text{=g(z)(1-g(z))=}{1}/{4}\)

在神经网络中\(a= g(z)\); \(g{{(z)}^{'}}=\frac{d}{dz}g(z)=a(1-a)\)

1. Tanh activation function

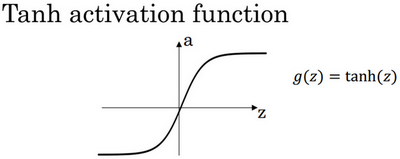
图3.8.2

其具体的求导如下：

公式3.26：

$g(z) = tanh(z) = \frac{e^{z} - e^{-z}}{e + e^{-z}} $

公式3.27：

\(\frac{d}{{d}z}g(z) = 1 - (tanh(z))^{2}\)

注：

当\(z\) = 10或\(z= -10\) \(\frac{d}{dz}g(z)\approx0\)

当\(z\) = 0, \(\frac{d}{dz}g(z)\text{=1-(0)=}1\)

在神经网络中;

3）Rectified Linear Unit (ReLU)

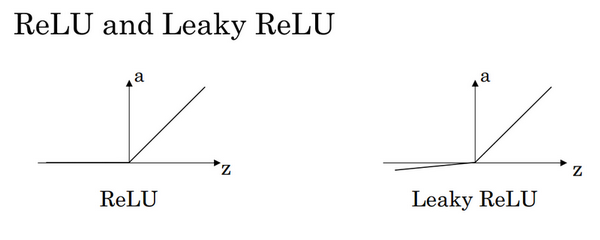
\(g(z) =max (0,z)\)

\[g(z)^{'}=
\begin{cases}
0& \text{if z < 0}\\
1& \text{if z > 0}\\
undefined& \text{if z = 0}
\end{cases}
\]

注：通常在\(z\)= 0的时候给定其导数1,0；当然\(z\)=0的情况很少

4）Leaky linear unit (Leaky ReLU)

与ReLU类似

\[g(z)=\max(0.01z,z) \\
\\
\\
g(z)^{'}=
\begin{cases}
0.01& \text{if z < 0}\\
1& \text{if z > 0}\\
undefined& \text{if z = 0}
\end{cases}
\]

注：通常在\(z = 0\)的时候给定其导数1,0.01；当然\(z=0\)的情况很少。