机器人多目标包围问题(MECA)新算法：基于关系图深度强化学习

摘要：中科院自动化所蒲志强教授团队，提出一种基于关系图的深度强化学习方法，应用于多目标避碰包围问题(MECA)，使用NOKOV度量动作捕捉系统获取多机器人位置信息，验证了方法的有效性和适应性。研究成果在2022年ICRA大会发表。

在多机器人系统的研究领域中，包围控制是一个重要的课题。其在民用和军事领域都有广泛的应用场景，包括协同护航、捕获敌方目标、侦察监视、无人水面舰艇巡逻狩猎等。

这些应用的核心问题是如何控制一个多机器人系统，涉及多目标分配，同时解决目标包围和避碰子问题。这是一个巨大的挑战，特别是对于分散的多机器人系统。

中科院自动化所蒲志强教授团队在2022年ICRA大会发表论文，提出了一种基于关系图的深度强化学习方法，对各种条件下的多目标避碰包围(MECA)问题具有良好的适应性。

定义任务

该研究定义了一个MECA任务，即在具有L个静态障碍物(黑色圆圈)的环境中，由N个机器人(绿色圆圈)组成的多机器人系统，协同包围K (1 < K < N)个静止或运动的目标(红色圆圈)。

所有机器人需要自动形成多组，包围所有目标，每组需要形成圆形队形，包围一个独立的目标，同时避免碰撞。这涉及到以下三个子问题：

1) 动态多目标分配与分组

2) 每组分别包围

3) 相互之间避免碰撞

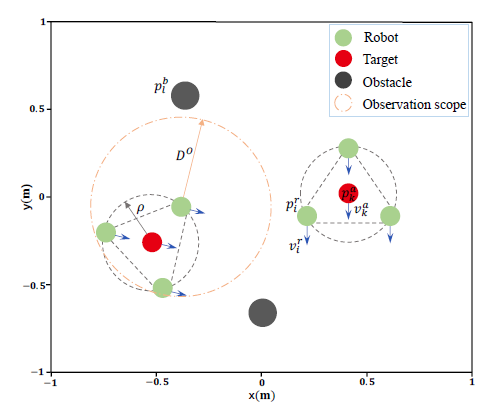
分散式多机器人系统的MECA图解

方法框架

在MECA问题中，存在三种类型的实体，即机器人、目标和障碍物。不同的实体对机器人有不同的影响关系，例如避障、包围目标、与其他机器人合作等。

研究提出了一种基于机器人级和目标级关系图(RGs)的DRL分散方法，命名为MECA-DRL-RG方法。

具体而言：

利用图注意网络(GATs)对机器人级RGs进行建模和学习，该RGs由每个机器人与其他机器人、目标和障碍物之间的三个异构关系图组成。
利用GAT构建目标级RG，构建机器人与各目标之间的空间关系。目标的运动由目标级RG建模，并通过监督学习进行学习，以预测目标的轨迹。
此外，定义了一个知识嵌入式复合奖励函数，解决MECA中的多目标问题。采用基于集中式训练和去中心化执行框架的演员-评论家训练算法对策略网络进行训练。

MECA-DRL-RG方法的整体结构

实验验证

研究团队分别进行了仿真实验和真实环境实验。在真实实验中，情景设置为：6个机器人在有2个障碍物的环境中包围2个移动的目标。机器人的位置和速度数据由NOKOV度量动作捕捉系统提供。

6个机器人在有2个障碍物的环境中包围2个移动目标

仿真实验和真实实验都验证了，相比于其他方法，MECA-DRL-RG方法使机器人能够从周围环境中，学习异构空间关系图，并预测目标的轨迹，从而促进每个机器人对其周围环境的理解和预测。证实了MECA-DRL-RG方法的有效性。

并且，无论机器人、障碍物或目标的数量增加，抑或是目标的移动速度加快，MECA-DRL-RG方法都表现出良好的性能，具有广泛的适应性。

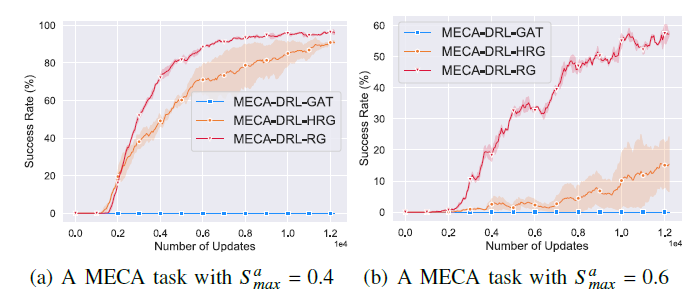
MECA-DRL-RG方法训练曲线

参考文献：

T. Zhang, Z. Liu, Z. Pu and J. Yi, "Multi-Target Encirclement with Collision Avoidance via Deep Reinforcement Learning using Relational Graphs," 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 2022, pp. 8794-8800, doi: 10.1109/ICRA46639.2022.9812151.