dp线段树优化

Description

The little cat takes over the management of a new park. There is a large circular statue in the center of the park, surrounded by N pots of flowers. Each potted flower will be assigned to an integer number (possibly negative) denoting how attractive it is. See the following graph as an example:

(Positions of potted flowers are assigned to index numbers in the range of 1 ... N. The i-th pot and the (i + 1)-th pot are consecutive for any given i (1 <= i < N), and 1st pot is next to N-th pot in addition.)

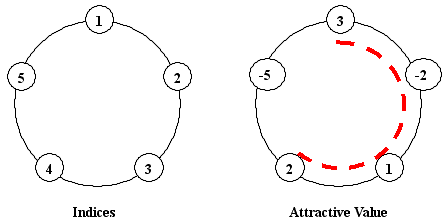
The board chairman informed the little cat to construct "ONE arc-style cane-chair" for tourists having a rest, and the sum of attractive values of the flowers beside the cane-chair should be as large as possible. You should notice that a cane-chair cannot be a total circle, so the number of flowers beside the cane-chair may be 1, 2, ..., N - 1, but cannot be N. In the above example, if we construct a cane-chair in the position of that red-dashed-arc, we will have the sum of 3+(-2)+1+2=4, which is the largest among all possible constructions.

Unluckily, some booted cats always make trouble for the little cat, by changing some potted flowers to others. The intelligence agency of little cat has caught up all the M instruments of booted cats' action. Each instrument is in the form of "A B", which means changing the A-th potted flowered with a new one whose attractive value equals to B. You have to report the new "maximal sum" after each instruction.

Input

There will be a single test data in the input. You are given an integer N (4 <= N <= 100000) in the first input line.

The second line contains N integers, which are the initial attractive value of each potted flower. The i-th number is for the potted flower on the i-th position.

A single integer M (4 <= M <= 100000) in the third input line, and the following M lines each contains an instruction "A B" in the form described above.

Restriction: All the attractive values are within [-1000, 1000]. We guarantee the maximal sum will be always a positive integer.

Output

For each instruction, output a single line with the maximum sum of attractive values for the optimum cane-chair.

Sample Input

5

3 -2 1 2 -5

4

2 -2

5 -5

2 -4

5 -1

Sample Output

题目大意：给定一个环形数列，每次更改一个数，求其最大子段和（长度不能为 n ）

数据的$n,m$极大，$O(n^2)$的方法就否决了。第一次知道线段树可求最大子段和，线段树tql。

环形最大子段和在不破坏原有队列情况下，只有两种可能，1.中间的一段 2.左端前缀和+右端前缀和

先不管长度，于是我们可以维护左最大前缀，右最大前缀，区间最大值，区间和，则pushup函数就出来了：

tree[id].lmx=max(tree[ls].lmx,tree[ls].s+tree[rs].lmx);

tree[id].rmx=max(tree[rs].rmx,tree[rs].s+tree[ls].rmx);

tree[id].s=tree[ls].s+tree[rs].s;

tree[id].mx=max(tree[ls].mx,max(tree[rs].mx,tree[ls].rmx+tree[rs].lmx));

然后对于更新后输出结果讨论，只需要比较上述的两种可能就可以了。

还是得管长度，当长度为n时，我们需要减去最短的子段和，所以线段树也需要维护所有最小值：

tree[id].lmn=min(tree[ls].lmn,tree[ls].s+tree[rs].lmn);

tree[id].rmn=min(tree[rs].rmn,tree[rs].s+tree[ls].rmn);

tree[id].mn=min(tree[ls].mn,min(tree[rs].mn,tree[ls].rmn+tree[rs].lmn));

所以答案是中间的一段max即tree[1].mx，左端前缀和+右端前缀和即tree[1].s-tree[1].mn比大小

因为tree[1].mx有可能包含整个数列，所以当tree[1].mx=tree[1].s时只取左右端前缀和。（证明如下）

如果tree[1].sum<=0,则tree[1].maxsum分两种情况讨论：

1.tree[1].maxsum包含区间1~n，则与tree[1].sum等价，输出tree[1].sum-tree[1].minsum正确

2.tree[1].maxsum只包含区间1~n部分，因为tree[1].maxsum是确定的，且tree[1].maxsum=tree[1].sum,tree[1].minsum<0(因为tree[1].sum<0)，则

  tree[1].sum-tree[1].minsum仍大于等于tree[1].maxsum，结果仍正确

如果tree[1].sum>0，易证。

Code

#include<cstdio>

#include<iostream>

using namespace std;

const int N=1e5+5;

struct qh{

    int s,mx,mn,lmx,lmn,rmx,rmn;

}tree[N<<2];

inline int Rd(){

    int s=0,w=1;char ch=getchar();

    while (ch<'0'||ch>'9'){if(ch=='-') w=-1;ch=getchar();}

    while (ch>='0'&&ch<='9') s=(s<<1)+(s<<3)+ch-'0',ch=getchar();

    return s*w;

}

#define ls id<<1

#define rs ls|1

#define M (l+r>>1)

void pushup(int id){

    tree[id].s=tree[ls].s+tree[rs].s;

    tree[id].lmx=max(tree[ls].lmx,tree[ls].s+tree[rs].lmx);

    tree[id].lmn=min(tree[ls].lmn,tree[ls].s+tree[rs].lmn);

    tree[id].rmx=max(tree[rs].rmx,tree[rs].s+tree[ls].rmx);

    tree[id].rmn=min(tree[rs].rmn,tree[rs].s+tree[ls].rmn);

    tree[id].mx=max(tree[ls].mx,max(tree[rs].mx,tree[ls].rmx+tree[rs].lmx));

    tree[id].mn=min(tree[ls].mn,min(tree[rs].mn,tree[ls].rmn+tree[rs].lmn));

    return ;

}

void update(int id,int l,int r,int x,int v){

    if(l==r){

        tree[id].s=tree[id].mx=tree[id].mn=tree[id].lmx=tree[id].lmn=tree[id].rmx=tree[id].rmn=v;

        return ;

    }

    if(x<=M) update(ls,l,M,x,v);

    else update(rs,M+1,r,x,v);

    pushup(id);

}

#undef ls

#undef rs

#undef M

int main(){

    int n=Rd();

    for(int i=1,x;i<=n;i++) x=Rd(),update(1,1,n,i,x);

    int m=Rd();

    while (m--){

        int a=Rd(),b=Rd();

        update(1,1,n,a,b);

        if(tree[1].mx==tree[1].s) printf("%d\n",tree[1].s-tree[1].mn);

        else printf("%d\n",max(tree[1].mx,tree[1].s-tree[1].mn));

    }

    return 0;

}

Start :2022.09.07:16:20

Finish:2022.09.07:17:22