力扣32(java)-最长有效括号（困难）

题目：

给你一个只包含 '(' 和 ')' 的字符串，找出最长有效（格式正确且连续）括号子串的长度。

示例 1：

输入：s = "(()"
输出：2
解释：最长有效括号子串是 "()"
示例 2：

输入：s = ")()())"
输出：4
解释：最长有效括号子串是 "()()"
示例 3：

输入：s = ""
输出：0

提示：

0 <= s.length <= 3 * 104
s[i] 为 '(' 或 ')'

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/longest-valid-parentheses
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路：

 一、栈

参照@笨猪爆破组 大佬的题解

由于该题需要求的是最长有效括号的子串长度，那么栈中不需要存放左括号，而是存放左括号的下标。当遇到右括号时，就弹出栈顶的左括号索引，然后就更新有效长度 = 当前右括号的索引 - 栈顶左括号的索引 + 1，在更新一下最大有效长度

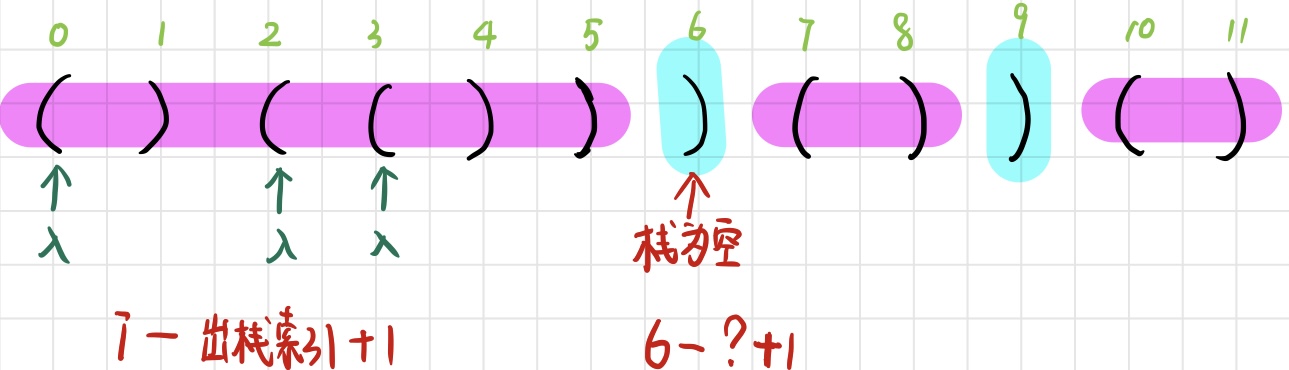
但是当在索引6遇到右括号时，此时栈为空，找不到与之匹配的左括号了，这时前面索引5计算的长度为4，但是实际最大长度为6，这时不知该如何继续计算...

所以就需要在最开始的时候栈里设置一个“参照物”为-1，计算有效长度 = 当前右括号的索引 - 出栈后新的栈顶索引，在后面栈为空时遇到右括号，就将右括号的索引作为新的参照物压入栈中。

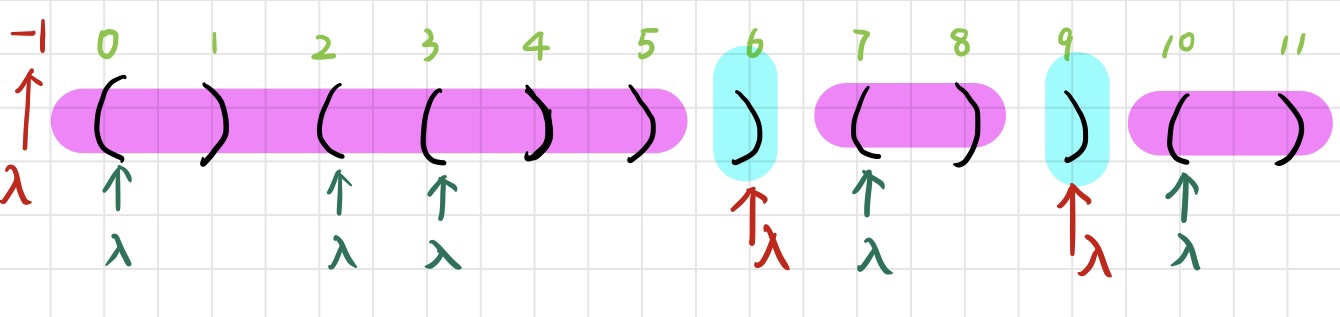
前面步骤省略

当遇到索引5时，有效长度为= 5 - (-1) = 6；

当遇到索引6时，就会将栈顶元素 -1 弹出，栈为空，将6压栈；

当遇到索引7时，7入栈；

当遇到索引8时，7出栈，有效长度= 8 - 6 = 2，更新最大长度仍为6；

当遇到索引9时，弹出栈顶元素6，栈为空，将9压栈；

当遇到索引10时，10入栈；

当遇到索引11时，10出栈，有效长度 = 11 - 9 = 2，更新最大长度仍为6；

遍历完毕，返回最大长度6。

代码：

 1 class Solution {
 2     public int longestValidParentheses(String s) {
 3         int n = s.length();
 4         Deque<Integer> stack = new ArrayDeque<>();
 5         //最先让-1入栈作为参照物
 6         stack.addLast(-1);
 7         int max = 0;
 8         for(int i = 0; i < n; i++){
 9             char c = s.charAt(i);
10             if(c == '('){
11                 stack.addLast(i);
12             }else{
13                 stack.pollLast();
14                 if(stack.isEmpty()){
15                     //栈为空就把右括号索引入栈,作为新的参照物
16                     stack.addLast(i);
17                 }else{
18                     max = Math.max(max,i - stack.peekLast());
19                 }
20             }
21         }
22         return max;
23     }
24 }

 二、动态规划（不好理解）

定义dp[i] : 以s[i]结尾的最长有效子串的长度。

子串的末位s[i] 要么是 '('，要么是 ')',下面分情况讨论：

1.s[i]是 '('，以左括号结尾一定不是有效子串，即 dp[i] = 0；

2.s[i]是 ')'，这时候就需要考虑前一个子串的末位 s[i-1]：

• 如果 s[i-1] 是 '('，刚好与 s[i] 组成一对，最长有效长度至少也得为2，这时候又需要考虑再前面一个子串末位 s[i-2]：
  • 如果 s[i-2]不存在，则有效长度为2，即 dp[i] = 2；
  • 如果s[i-2]存在，则需要加上以s[i-2]结尾的有效长度，即dp[i] = dp[i-2] + 2;

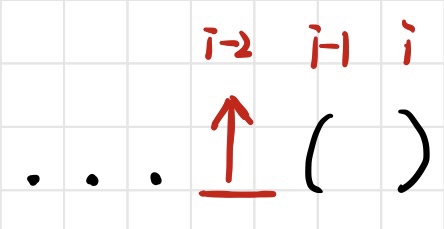
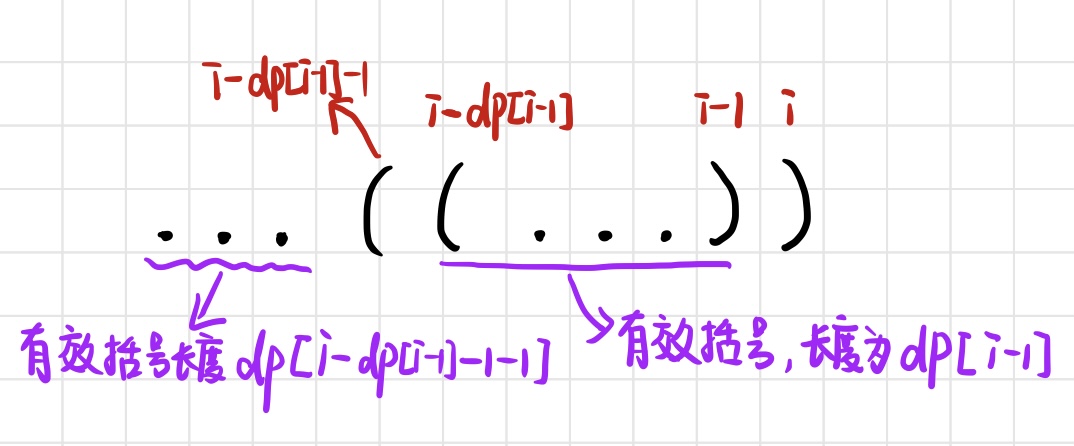
如果 s[i-1]是 ')',以s[i-1]结尾的最长有效长度为 dp[i-1]，这时候就需要看第 i -dp[i-1] - 1这个位置的字符即 s[i-dp[i-1]-1]：
• 如果 s[i-dp[i-1]-1]处的字符不存在或者为 ')'，就不能与s[i]处的 ')'配对，即dp[i] = 0；
• 如果 s[i-dp[i-1]-1]处的字符为 '('，与s[i]处的 ')'配对，这时候dp[i] 至少也得为dp[i-1] +2,这时候就看s[i-dp[i-1]-1-1] (s[i-dp[i-1]-2])是否存在：
  • s[i-dp[i-1]-2] 存在，dp[i] = dp[i-dp[i-1] -2] + dp[i-1] + 2；
  • s[i-dp[i-1]-2]不存在，dp[i] = dp[i-1] + 2；

 代码：

 1 class Solution {
 2     public int longestValidParentheses(String s) {
 3         int n = s.length();
 4         int ans = 0;
 5         int[] dp = new int[n];
 6         for(int i = 1; i < n; i++){
 7             if(s.charAt(i) == ')'){
 8                 if(s.charAt(i-1) == '('){
 9                     dp[i] = (i >= 2) ? dp[i-2]+2 : 2;
10                 }else if(i - dp[i-1] > 0 && s.charAt(i- dp[i-1] -1)== '('){
11                 //保证第i - dp[i-1]这个位置之前还有字符且前一个字符还必须为左括号
12                 dp[i] = dp[i-1] + 2 + (i-dp[i-1] - 2 >= 0 ? dp[i-dp[i-1] -2] : 0);
13                 }
14             ans = Math.max(ans, dp[i]);
15             }
16         }
17         return ans;
18     }
19 }