SkipList原理与实现

机制

链表中查询的效率的复杂度是O(n), 有没有办法提升这个查询复杂度呢? 最简单的想法就是在原始的链表上构建多层索引.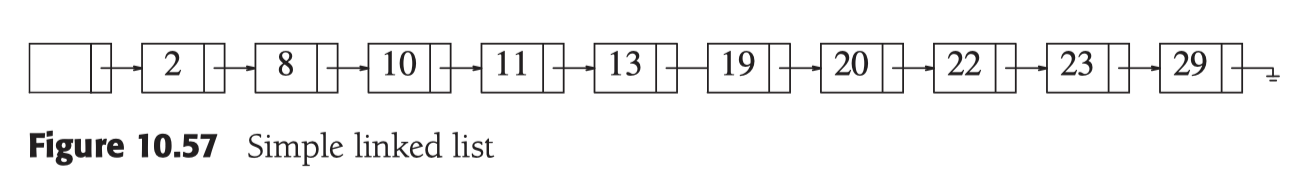

在level 1(最底层为0), 每2位插入一个索引, 查询复杂度便是 O(N/2 + 1)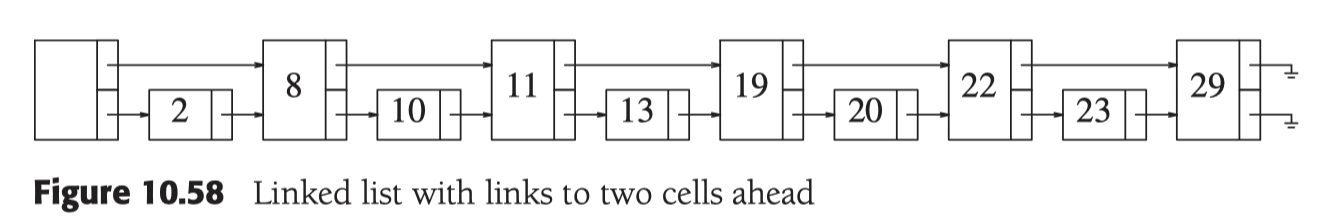

在level 2, 每四位插入一个索引, 查询复杂度便是 O(N/4 + 2)

那么推广开来, 如果我们有这样的一组链表, 在level i, 每间隔第 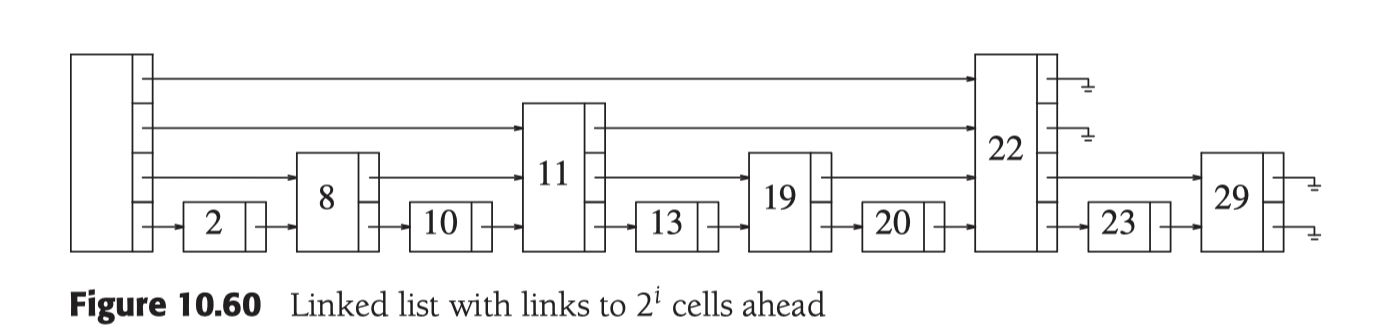元素就有一个链接 在level 1, 每一个节点之间有一个链接 在level 2, 每两个节点之间有一个链接 在level 3, 每四个节点之间有一个链接 在level 4, 每八个节点之间有一个链接. 这样我们可以看到, 每向上一层, 数据量就减少了 1/2, 所以查询的过程就近似变成了2分查找, 查询性能就变成了稳定的O(logN). 索引的存储空间为 其中

两式相减得到 所以 所以 因此这样的数据结构总的空间复杂度为 2n - 2.

但是这样的数据结构存在一个问题, 严格要求每一层按照 的间隔链接很难在持续插入的过程中维护.

当插入一个新元素的时候, 需要为他分配一个新的节点, 此时我们需要决定该节点是多少阶的. 通过观察 Figure 10.60 可以发现, 有1/2的元素是1阶的, 有 1/4 的元素是2阶的, 所以大约 的节点是第 i 阶的. 那么根据这个性质, 我们就可以通过随机统计的方式来判断新元素应该插入的阶数. 最容易得做法就是抛一枚硬币直到正面出现并把抛硬币的总次数用作该节点的阶数.

连续抛i次才出现正面的概率是 , 而的节点是属于第 i 阶的.

通常的计算阶数的方法

/**
 * 这个函数返回的是levelCount, 最小为1, 表示不构建索引.
 *
 * <p>
 * <li>1/2 概率返回1 表示不用构建索引
 * <li>1/2 概率返回2 表示构建一级索引
 * <li>1/4 概率返回3 表示构建二级索引
 * <li>1/8 概率返回4 表示构建三级索引
 *
 * @return
 */
private int randomLevel() {
    int level = 1;
    while (Math.random() < SKIPLIST_P && level < MAX_LEVEL) {
        level++;
    }
    return level;
}

通常p取值为 1/2 或者 1/4 表示两层之间的数据分布概率, Math.random()随机返回一个0-1之间的数, 这个就是模拟不断抛硬币的过程, height 为累计的抛硬币的次数.

因此跳表的实现, 是利用了随机化算法来计算新插入节点的阶数, 而这个阶数的数学期望能保证每一层数据能随机化的递减 1/2, 通过这样来保证最终插入和查找复杂度的期望都为 O(logN).

相比于红黑树 优势

1. 插入 查找 删除的复杂度和红黑树一样

2. 区间查找的效率更高

3. 代码实现更简单

4. 并且可以通过插入节点阶数生成的策略来平衡时间和空间复杂度的不同需求. 比如我们可以让每一层的数据为下一层的1/3. 这种情况下索引存储量 为 n/3 + n/9 + n/27 + ... 2 = n / 2 空间占用就缩小一半.

劣势

1. 跳表的内存占用相比会大一点, 不过因为索引其实可以只存储key和指针, 实际的空间开销往往没有那么大

实现

查找

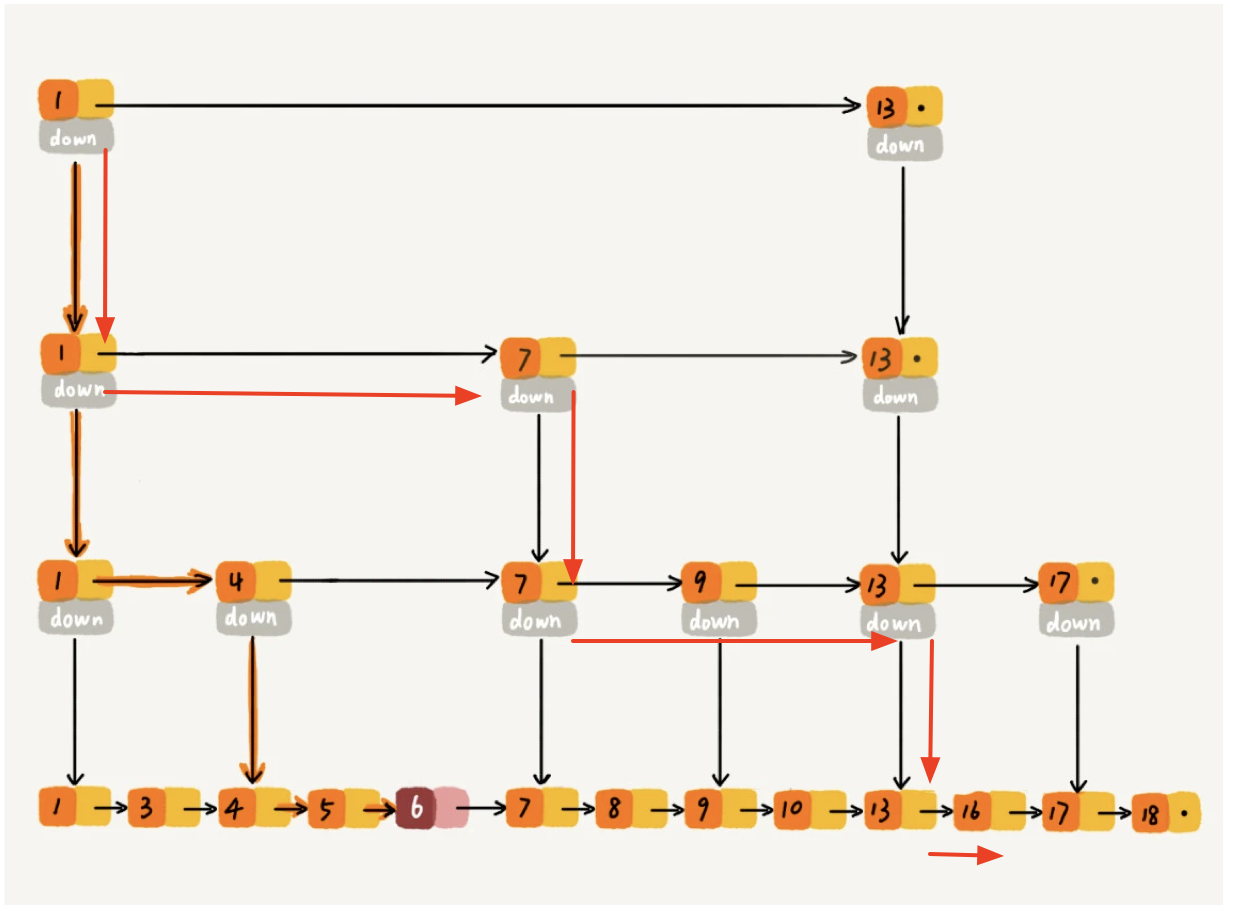例如查找16

1. 从head处开始查找, 同一层中遍历向前直到next节点为空或者next节点的value大于当前值

2. 跳转到level + 1的索引处, 继续上述流程

3. 最后一定会到达level 0. 指针非空则找到了相应的value

插入

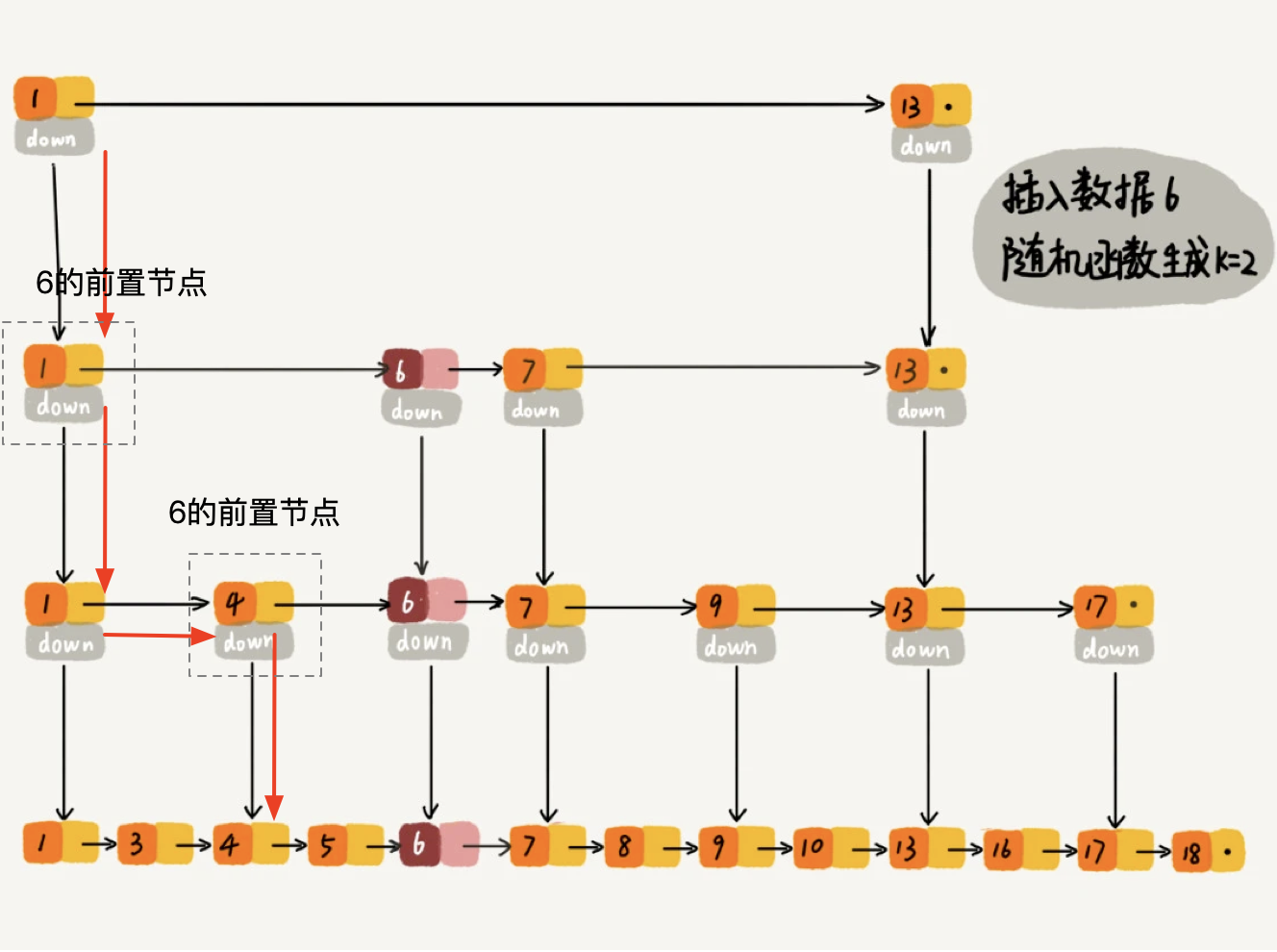
1. 通过随机函数生成此value插入的高度为2.

2. 同查找一样的遍历流程, 找到比6大的那个位置. 在此过程中, 每一次向下迭代需要记录转折点如图中的1和4.这两个节点会作为6的前置节点

3. 将新value的next指向原来前置节点的next, 将原来前置节点的next指向新的节点

4. 同时新生成的level是可能高于原始高度的

删除

删除相比插入更简单, 在遍历每一层的时候不需要单独去记录前置节点了. 虽然以下实现是记录了前置节点后统一更新的, 但我感觉是没有必要的, delete可以改成 https://github.com/wangzheng0822/algo/blob/master/java/17_skiplist/SkipList.java

public void delete2(int value) {
    Node p = head;
    // 找到前置节点
    for (int i = levelCount - 1; i >= 0; i--) {
        while (p.forwards[i] != null && p.forwards[i].value < value) {
            p = p.forwards[i];
        }
        if (p.forwards[i] != null && p.forwards[i].value == value) {
            p.forwards[i] = p.forwards[i].forwards[i];
        }
    }
​
    // head 指向为空的节点都剔除.
    while (levelCount > 1 && head.forwards[levelCount] == null) {
        levelCount--;
    }
}

工业实现

redis的sorted set hbase中内存的有序集合 java ConcurrentSkipListSet ConcurrentSkipListMap

参考

<数据结构与算法分析 Java描述> 10.4.2

<HBase原理与实践> 2.1 跳跃表

王争数据结构与算法之美#17

Skip List--跳表（全网最详细的跳表文章没有之一）

https://zhuanlan.zhihu.com/p/33674267