【LeetCode二叉树#06】获取二叉树的所有路径（分析递归中的回溯机制）

二叉树所有路径

力扣题目链接(opens new window)

给定一个二叉树，返回所有从根节点到叶子节点的路径。

说明: 叶子节点是指没有子节点的节点。

示例:

思路

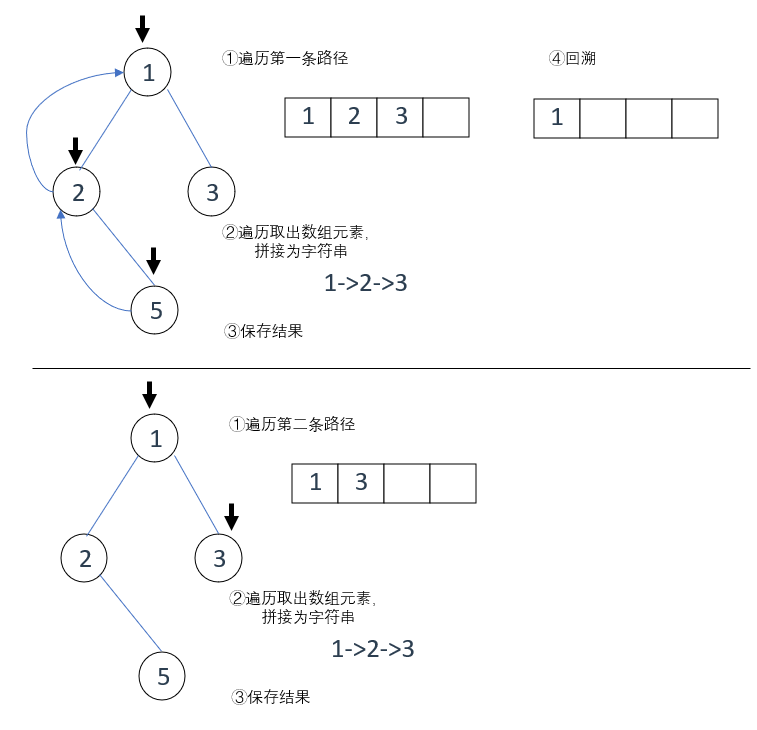
根据题意，每次遍历至子节点，我们都需要返回根节点然后从另外一条路径继续遍历

关键点是：返回，实现这个机制需要使用递归与回溯

且最后输出结果的顺序是根节点->子节点->叶子节点，也就是从上到下的顺序，因此可以使用前序遍历

代码

先写递归逻辑，还是递归的三部曲

1、确定递归函数的参数、返回值

需要传入的是根节点，然后记录每一条路径path，并保存至结果数组res；

不涉及返回值

void  traversal(TreeNode* node, vector<int>& path, vector<string>& res){

}

在记录路径时，一开始我们是通过递归不断保存路径上每个节点的值，因此需要使用数组来保存

之后按照题目要求，输出时需要将一段路径用"->"连接，因此结果数组中保存的应该是字符串类型的路径

2、确定终止条件

由题意可知，从根节点到叶子节点才算构成一条完整路径

那么我们的终止条件可以设置为：当前节点是否为叶子节点

即

void  traversal(TreeNode* node, vector<int>& path, vector<string>& res){
    if(node->left == NULL && node->right == NULL){//左右子节点均为空时
        //终止时的处理代码
    }
}

因为使用vector来存放路径，所以在结束一条路径的遍历时，我们需要将path数组的值遍历出来，转换为string并拼接箭头

最后存放至res结果数组中。

void  traversal(TreeNode* node, vector<int>& path, vector<string>& res){
    if(node->left == NULL && node->right == NULL){//左右子节点均为空时
        //终止时的处理代码
        //定义一个string变量存放路径字符串
        string spath;
        //遍历path数组
        for(int i = 0; i < path.size() - 1; ++i){
            spath += to_string(path[i]);//将元素转换为字符串类型
            spath += "->";//拼接箭头
        }
        //单独把最后一个节点（叶子节点）接上，因为其后不需要接箭头，所以不放在循环里
        spath += to_string(path[path.size() - 1]);
        //保存一条路径至结果数组
        res.push_back(spath);
        return;//结束
    }
}

3、确定单层处理逻辑

这里的遍历逻辑是前序遍历，中左右

按理来说，“中”（处理中间节点）应该和“左右”一块放在终止条件后面

但是，这里情况比较特殊，中间节点就是我们需要记录的路径节点，因此需要先将其放入path中，即

void  traversal(TreeNode* node, vector<int>& path, vector<string>& res){
    path.push_back(cur->val);//将当前节点值放入path
    if(node->left == NULL && node->right == NULL){//左右子节点均为空时
        ...
    }
}

然后，左右的遍历处理与往常一样，不过得先判断左右子节点是否存在

void  traversal(TreeNode* node, vector<int>& path, vector<string>& res){
    path.push_back(cur->val);//将当前节点值放入path
    if(node->left == NULL && node->right == NULL){//左右子节点均为空时
    	//终止时的处理代码
        //定义一个string变量存放路径字符串
        string spath;
        //遍历path数组
        for(int i = 0; i < path.size() - 1; ++i){
            spath += to_string(path[i]);//将元素转换为字符串类型
            spath += "->";//拼接箭头
        }
        //单独把最后一个节点（叶子节点）接上，因为其后不需要接箭头，所以不放在循环里
        spath += to_string(path[path.size() - 1]);
        //保存一条路径至结果数组
        res.push_back(spath);
        return;//结束
    }

    if(node->left != NULL){
        traversal(node->left, path, res);
    }

    if(node->right != NULL){
        traversal(node->right, path, res);
    }
}

然后，重要的点来了

前面我们在梳理思路的时候分析了，当找到叶子节点后，我们就在path数组中记录了一条完整路径

那么此时我们需要将记录的节点“弹出”，直到只剩下根节点，然后再去寻找系下一条路径

上述过程即为 回溯

如何实现回溯呢？我们在前序遍历中遍历左右子节点时使用了 递归 ，那么当递归一层一层的执行，最后我们会找到某个叶子节点

此时按照递归的逻辑，最内层的递归会将获取到的结果层层返回

因为我们在最里层递归中已经将完整路径字符串保存到结果数组，所以我们可以利用递归返回值的过程，将每层递归记录的路径节点逐个pop掉

最后只剩下根节点，然后开始下一条路径的遍历

void  traversal(TreeNode* node, vector<int>& path, vector<string>& res){
    path.push_back(node->val);//将当前节点值放入path
    //左右子节点均为空时找到叶子节点
    if(node->left == NULL && node->right == NULL){//已终止递归，开始保存记录的路径节点
    	//终止时的处理代码
        //定义一个string变量存放路径字符串
        string spath;
        //遍历path数组
        for(int i = 0; i < path.size() - 1; ++i){//减一是因为最后一个节点需要在循环外处理
            spath += to_string(path[i]);//将元素转换为字符串类型
            spath += "->";//拼接箭头
        }
        //单独把最后一个节点（叶子节点）接上，因为其后不需要接箭头，所以不放在循环里
        spath += to_string(path[path.size() - 1]);
        //保存一条路径至结果数组
        res.push_back(spath);
        return;//结束
    }

    if(node->left != NULL){
        traversal(node->left, path, res);
        res.pop_back();//在递归返回过程中（回溯）不断删除之前记录的路径节点
    }

    if(node->right != NULL){
        traversal(node->right, path, res);
        res.pop_back();
    }
}

完整代码

class Solution {
public:
    //创建递归函数
    //确定递归函数的参数和返回值
    void traversal(TreeNode* node, vector<int>& path, vector<string>& res){
        path.push_back(node->val);//将当前节点的值放入path //中
        //确定终止条件
        //左右子节点均为空时找到叶子节点
        if(node->left == NULL && node->right == NULL){//已终止递归，开始保存记录的路径节点
            //定义变量保存路径字符串
            string spath;
            //遍历path取出记录的路径节点
            for(int i = 0; i < path.size() - 1; ++i){//减一是因为最后一个节点需要在循环外处理
                spath += to_string(path[i]);//将元素转换为字符串类型
                spath += "->";//使用箭头拼接
            }
            //单独把最后一个节点（叶子节点）接上，因为其后不需要接箭头，所以不放在循环里
            spath += to_string(path[path.size() - 1]);
            //保存一条完整路径
            res.push_back(spath);
            return;
        }
        //确定单层处理逻辑
        if(node->left){//左
            traversal(node->left, path, res);
            path.pop_back();//在递归返回过程中（回溯）不断删除之前记录的路径节点
        }
        if(node->right){//右
            traversal(node->right, path, res);
            path.pop_back();
        }
    }

    vector<string> binaryTreePaths(TreeNode* root) {
        vector<int> path;
        vector<string> res;
        traversal(root, path, res);
        return res;
    }
};

注意点：

1、真的，别忘了输入参数时以引用方式输入

2、一般在递归三部曲的第三步：确认当前递归层的处理逻辑中，都会再次调用递归函数