Basic concepts of complex number

目录

• 虚数的引入
• 复数和虚数的关系
• Example - 分辨一个数
• 判断两个复数是否相等的条件
• 共轭复数
• 复数的几何意义、复平面的认识
• 求复数的模
• Reference

---

虚数的引入

假设有一个数，可以叫它X数，但是不太好听，改成高大上一点，叫成虚数吧！

对它的定义如下：

• 虚数=i
• \(i^2\) = -1

这样搞有什么好处吗？

假设想求出 \(\sqrt{-7}\)，在实数范围内没戏，但是有了这个虚数工具，那就好办了!

\(\sqrt{-7}\) = \(\sqrt{7*(-1)}\)

=\(\sqrt{7*i^2}\)

=\(\sqrt{7}i\)

在来一个案例：\((x-2)^2=-3\)

-3 = \(3*i^2\)

则：x-2 = $ \pm \sqrt{3*i^2} $

x-2 = $ \pm \sqrt{3}i $

x = 2 $ \pm \sqrt{3}i $

先不说现实的意义，反正就是厉害，就是强！

复数和虚数的关系

复数的定义：

z=a+bi;

复数的定义：

必须由实部和虚部组合起来的，才是复数。

既然是组合起来的，那么就可以分割出来：

• a 是实部；
  • 里面都是实数；
• bi 是虚部；
  • 里面的 b 是实数；
  • 里面的 i 是虚数；
  • 所以实数+虚数才是一个虚部。

分割完发现，它里面组合的元素还挺多的，与其说是它一个数，更不如说它是一个未经过运算的代数式！

复数里面实数虚数的判定条件：

b = 0 , 那么z=a+bi 是一个实数；

b ≠ 0 , 那么bi 是一个纯虚数；

Example - 分辨一个数

分辨下面这些数都是什么数？比如是实数，还是虚数、复数...

• $3-\sqrt{3} $
• \((2-\sqrt{7})i\)
• \(π+i\)
• 0

判断两个复数是否相等的条件

if a+bi = c+di ，

then a=c,b=d

共轭复数

已经在别的文章介绍过了，这里略。

https://www.cnblogs.com/mysticbinary/p/17191719.html

复数的几何意义、复平面的认识

先认识复平面，复平面和平面直角坐标系是一样的，无非是把原先的y轴改叫虚轴而已，原先的x轴该叫成实轴。

一个复数，有实部和虚部，刚好可以将他们转换成复平面的坐标 (实部，虚部)，

比如 A=6+4j 转换成复平面的坐标为：A(6,4j) ，那么就可以将这个坐标套入到复平面中去，

在认识向量 \(\overrightarrow{OP}\)

初次看到这个向量，可以理解为 这根斜线就是向量，随着认识的深入，发现，

这根斜线类似实数的绝对值概念，是复数在绝对值概念的推广，因为这个P(x,y)点到原点O的距离就是绝对值。

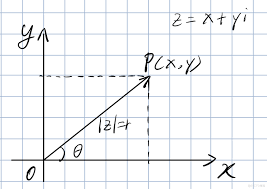
复数的辐角是指复数在复平面上对应的向量和正向实数轴所成的有向角。

"幅角"和"辐角"在大多数情况下可以互换使用，表示复数与实轴之间的角度，具体使用哪个术语可能取决于上下文和个人偏好。

求复数的模

求向量的长度，就是求复数的模。

Reference

复数的几何意义-课件

https://max.book118.com/html/2017/0517/107417075.shtm