题解报告：Luogu P3368 【模板】树状数组 2（区间修改，单点查询）

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数数加上x

2.求出某一个数的值

输入输出格式

输入格式：

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含2或4个整数，表示一个操作，具体如下：

操作1：格式：1 x y k 含义：将区间[x,y]内每个数加上k

操作2：格式：2 x 含义：输出第x个数的值

输出格式：

输出包含若干行整数，即为所有操作2的结果。

输入输出样例

输入样例#1：

输出样例#1：

6

10

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=10000，M<=10000

对于100%的数据：N<=500000，M<=500000

样例说明：

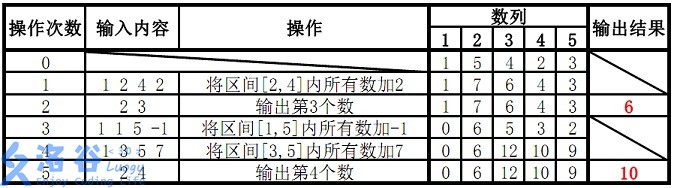
故输出结果为6、10

解题思路：前面已经讲过树状数组的单点修改，单点(区间)查询了。对于这道题要求的是区间修改，单点查询，怎么实现呢？首先来引入差分思想：假设原数组为A[]，差分数组为d[]，树状数组为C[]（C数组和单点修改那个树状数组一样记录着某段区间的总和），则差分数组d[i]=A[i]-A[i-1]（A[0]=0），即记录当前i位置的元素与前一个元素的差值，那么单点查询A[i]的值只需求d[i]的前缀和，即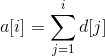(A[i]=d[1]+d[2]+...+d[i])。区间修改怎么利用差分数组呢？举个例子：设A[]={1,5,4,2,3}，那么d[]={1,,-1,-2,}，树状数组C[]={1,,-1,2,}，假设区间[2,4]中每个元素都加上2，则A[]={1,7,6,4,3}，那么d[]={1,,-1,-2,-1},树状数组C[]={1,,-1,4,-1}，修改后可以发现d数组中只有d[2]和d[5]改变了，而且d'[2]=d[2]+2=+2=，d'[5]=d[5]-2=-2=-1，并且区间[3,4]中每个元素的差值d[i]不变，这是因为区间[2,4]中每个元素是同时加上2的。因此，当对区间[l,r]中每个元素加上k（区间修改）时，因为A[l]与前一个元素A[l-1]的差值增加了k，A[r+1]与A[r]的差值减少了k，所以只需对差分树组进行操作：d[l]+=k,d[r+1]-=k，又因为树状数组维护着差分数组，所以实际效果上也是对树状数组进行操作：C[l]+=k,C[r+1]-=k。输入的时候只需将差分数组建树，其他代码操作基本不变，单点查询时只需调用一次query(x)即可。

AC代码：

 #include<bits/stdc++.h>

 using namespace std;

 typedef long long LL;

 const int maxn=5e5+;

 int n,m,p,x,y;LL k,C[maxn],val[maxn];//C为差分数组

 void add(int x,LL val){

     while(x<=n){C[x]+=val;x+=(x&-x);}

 }

 LL query(int x){

     LL ans=;

     while(x>){ans+=C[x];x-=(x&-x);}

     return ans;

 }

 int main(){

     while(~scanf("%d%d",&n,&m)){

         memset(C,,sizeof(C));val[]=;//注意val[0]要初始化为0

         for(int i=;i<=n;++i){

             scanf("%lld",&val[i]);

             add(i,val[i]-val[i-]);//差分思想

         }

         while(m--){

             scanf("%d",&p);

             if(p==){scanf("%d%d%lld",&x,&y,&k);add(x,k);add(y+,-k);}

             else{scanf("%d",&x);printf("%lld\n",query(x));}//单点查询

         }

     }

     return ;

 }