luogu 3415 祭坛

题目大意：

在平面上，有 n 个水晶柱，每个水晶柱可以用一个点表示

如果 4 个水晶柱依次相连可以构成一个四边形，满足其两条对角线分别平行于 x 轴和 y 轴，并且对角线的交点位于四边形内部（不包括边界）

那么这 4 个水晶柱就可以建立一个结界

其中，对角线的交点称作这个结界的中心

例如下左图中，水晶柱 ABCD 可以建立一个结界，其中心为 O

人们会把祭坛修建在最多层结界的保护中

其中不同层的结界必须有共同的中心，这些结界的边界不能有任何公共点，并且中心处也不能有水晶柱

这里共同中心的结界数量叫做结界的层数

为了达成这个目的，人们要先利用现有的水晶柱建立若干个结界，然后在某些结界的中心建立祭坛

例如上右图中，黑色的点表示水晶柱（注意 P 和 O 点不是水晶柱）。祭坛的一个最佳位置为 O 点，可以建立在 3 层结界中，其结界的具体方案见下左

当然，建立祭坛的最佳位置不一定是唯一，在上右图中，O 点左侧 1 单位的点 P 也可以建立一个在 3 层结界中的祭坛，见下右图

 

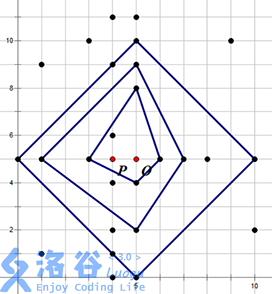
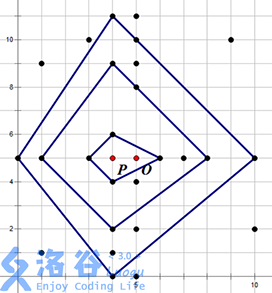
现在人们想知道：祭坛最佳选址地点所在的结界层数以及祭坛最佳的选址地点共有多少个

思路：

首先可以二分一下答案

然后对于每一个满足条件的点在它的上下左右四个方向一定有至少mid个点

对于上下或者左右是否满足条件 可以直接求出这个区间

对于另一个方向 使用扫描线与树状数组维护

 #include<iostream>
 #include<cstdio>
 #include<cmath>
 #include<cstdlib>
 #include<cstring>
 #include<algorithm>
 #include<vector>
 #include<queue>
 #define inf 2139062143
 #define ll long long
 #define MAXN 100100
 using namespace std;
 inline int read()
 {
     int x=,f=;char ch=getchar();
     while(!isdigit(ch)) {if(ch=='-') f=-;ch=getchar();}
     while(isdigit(ch)) {x=x*+ch-'';ch=getchar();}
     return x*f;
 }
 int n,up[MAXN],dn[MAXN],q[MAXN],cnt;
 vector<int> vec[MAXN];
 int c[MAXN],hsh[MAXN];
 int lowbit(int x) {return x&(-x);}
 void add(int x,int val) {for(int i=x;i<=n;i+=lowbit(i)) c[i]+=val;}
 int query(int x) {int res=;for(int i=x;i;i-=lowbit(i)) res+=c[i];return res;}
 int check(int x)
 {
     int res=,t;
     memset(hsh,,sizeof(hsh));
     memset(c,,sizeof(c));
     memset(up,,sizeof(up));
     memset(dn,,sizeof(dn));
     for(int i=;i<=cnt;i++)
         for(int j=;j<vec[q[i]].size();j++) dn[vec[q[i]][j]]++;
     for(int k=;k<=cnt;k++)
     {
         t=q[k];
         for(int i=;i<vec[t].size();i--)
         {
             dn[vec[t][i]]--;
             if((dn[vec[t][i]]<x||up[vec[t][i]]<x)&&hsh[vec[t][i]])
                 hsh[vec[t][i]]=,add(vec[t][i],-);
         }
         if(x-<vec[t].size())
         {
             int l=vec[t][x-],r=vec[t].size()-x;
             if(r<) goto ed;
             r=vec[t][r];
             if(r>&&l<=r-) res+=query(r-)-query(l);
         }ed:;
         for(int i=;i<vec[t].size();i--)
         {
             up[vec[t][i]]++;
             if(dn[vec[t][i]]>=x&&up[vec[t][i]]>=x&&!hsh[vec[t][i]]) {hsh[vec[t][i]]=,add(vec[t][i],);}
         }
     }
     return res;
 }
 int main()
 {
     n=read();int a,b;
     for(int i=;i<=n;i++)
     {
         a=read(),b=read();
         vec[a].push_back(b);
         q[++cnt]=a;
     }
     sort(q+,q+cnt+);
     cnt=unique(q+,q+cnt+)-q-;
     for(int i=;i<=cnt;i++) sort(vec[q[i]].begin(),vec[q[i]].end());
     int l=,r=n,ans=,res=;
     while(l<=r)
     {
         int mid=l+r>>;
         if(a=check(mid)) ans=mid,l=mid+,res=a;
         else r=mid-;
     }
     printf("%d\n%d",ans,res);
 }