龙哥量化：缠中说禅(缠论)K线包含处理

声明：看到研究非常细致深入的文章，转载到我的博客园，以便学习和研究。

（转载知乎的DennisWin）

缠中说禅技术理论包括两大部分：缠论形态学和缠论动力学。其中形态学是根本，动力学是辅助。缠论形态学从本质上讲就是几何学，包括两个相互联系又互为独立的系统：K线系统和均线系统。缠论形态学的K线系统，主要包括以下六个方面：K线的包含处理、分型、笔、线段、走势中枢、买卖点。缠论K线系统的操作思路是：通过K线包含处理，找出走势图中的顶底分型，依据顶底分型划分出笔，依据笔划分出线段，依据线段确立走势中枢，再根据走势中枢的情况，结合动力学部分的背驰及区间套，综合确定各类买卖点，然后依据各类买卖点执行实际交易。这就是缠中说禅技术理论的根本价值所在。

K线的包含处理

1. K线的关系

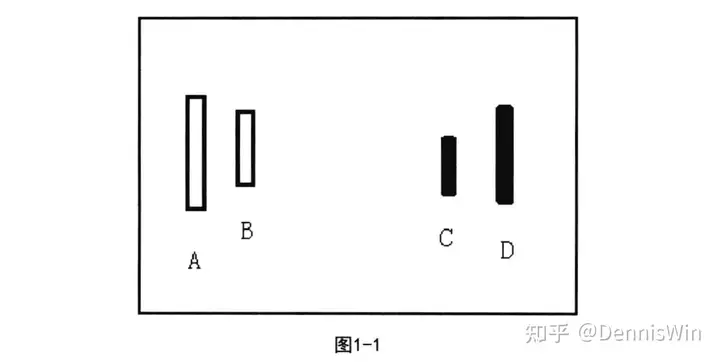
学习缠论K线系统分析方法，必须从K线的包含处理开始。只有理解和掌握了K线的包含处理，才能进入到分型、笔等其他内容的学习。打开K线走势图，能发现两相邻K线在实际走势中存在各种各样的关系。两相邻K线的包含关系给出一个定义：一根K线的高低点全部在其相邻K线的范围之内，那么这根K线和其相邻K线就为包含关系（注意：K线的高低点包括K线上下影线）。如图1-1所示，K线B的高低点全部在其相邻K线A的范围之内，则K线B和K线A为包含关系。K线C的高低点全部在其相邻K线D的范围之内，则K线C和K线D为包含关系。

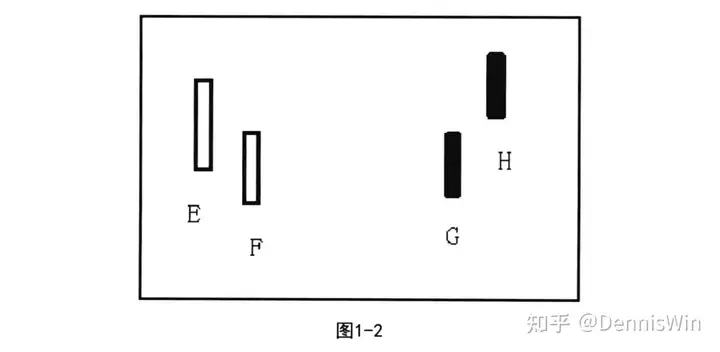
如图1-2所示，K线F的高低点没有全部在其相邻K线E的范围之内，则K线F和K线E不属于包含关系；K线G的高低点全部不在其相邻K线H的范围之内，则K线G和K线H不属于包含关系。

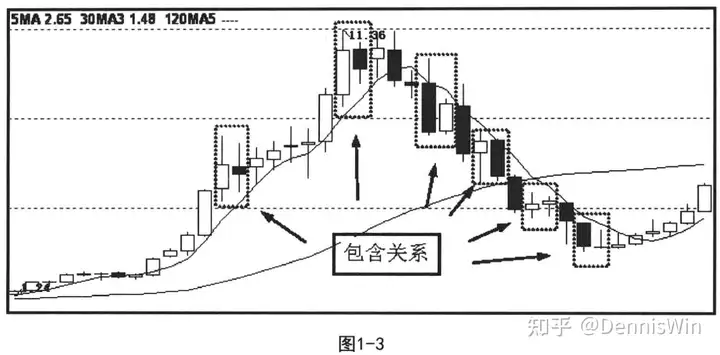
如图1-3所示，虚线框内的两相邻K线为包含关系。

2. K线的包含处理原则

K线走势图中，经常会看到一些有包含关系的K线。为了准确识别K线走势中的顶底分型，有必要对这些存在包含关系的K线进行包含处理。所谓包含处理，就是将有包含关系的两根K线合并成一根K线，即简化处理。K线包含处理分两种情况：向上处理和向下处理。

*向上处理

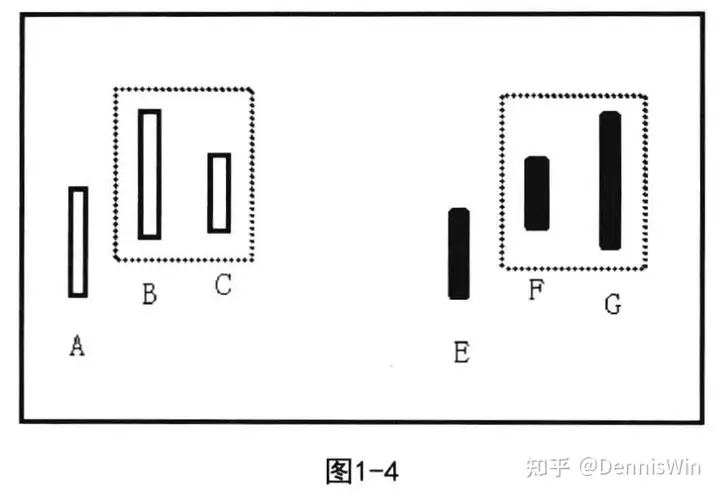
存在包含关系的两根K线合并时，当第一根K线的高点比其前一根具有非包含关系K线的高点高时，具有包含关系的两根K线采取向上处理。如图1-4所示，图左中B、C为具有包含关系的两相邻K线，当B的高点比其前一根具有非包含关系K线A的高点高时，则B、C取向上处理。图右中F、G为具有包含关系的两相邻K线，当F的高点比其前一根具有非包含关系k线E的高点高时，则FG取向上处理。

*向下处理

存在包含关系的两根K线合并时，当第一根K线的高点比前一根具有非包含关系K线的高点低时，具有包含关系的两根K线取向下处理。如图1-5所示，图左中B、C为具有包含关系的两根K线，当R的高点比前一根非包含关系K线A的高点低时，则B、C取向下处理。图右中F、G为具有包含关系的两根K线，当F的高点比前一根非包含关系K线E的高点低时，则F、G取向下处理。

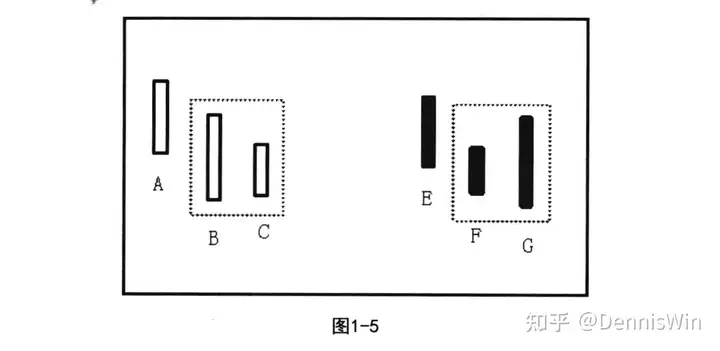
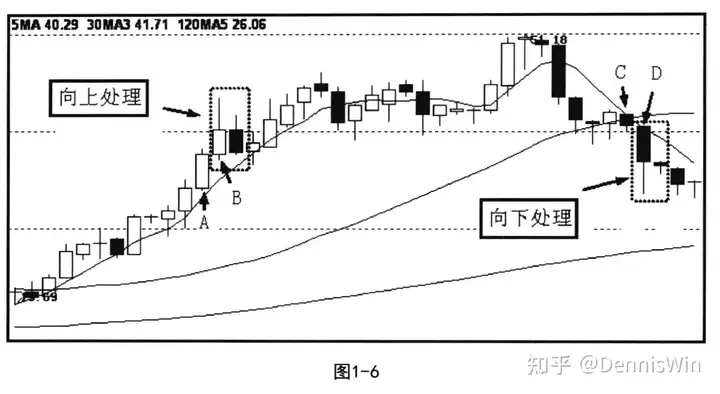
图1-6为向上处理及向下处理实图。图中B比A高，取向上处理；图中D比C低，取向下处理。

*向上处理的原则

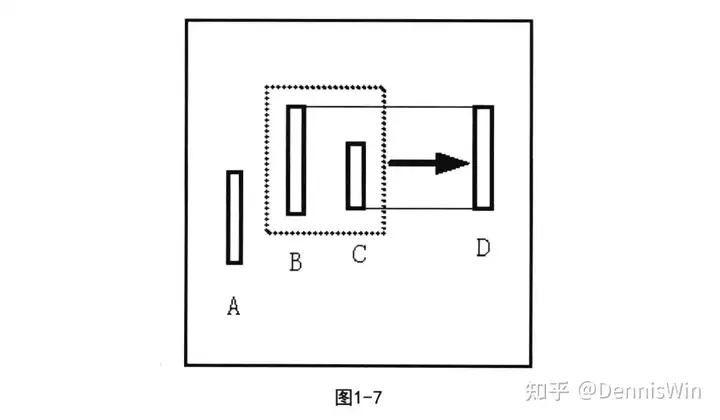
K线包含向上处理时，取两根K线中的最高点为高点，较低点为低点，合并成一根新K线。如图1-7所示，B、C向上处理，取两根K线中的最高点为高点，较低点为低点，合并成新K线D。

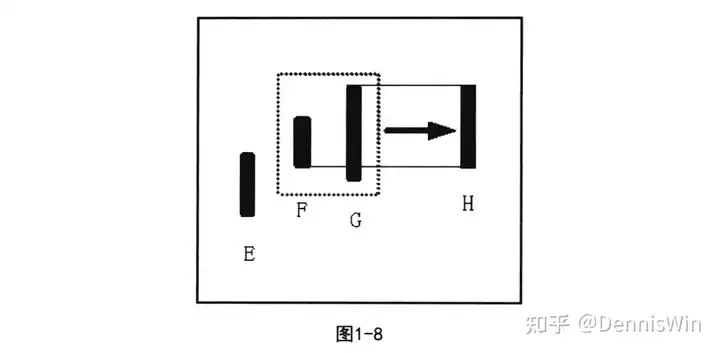
如图1-8所示，F、G向上处理，取两根K线中的最高点为高点，较低点为低点，合并成新K线H。

*向下处理的原则

K线包含向下处理，取两根K线中最低点为低点，较高点为高点，合并成一根新K线。如图1-9所示，B、C向下处理，取两根K线中最低点为低点，较高点为高点，合并成新K线D。

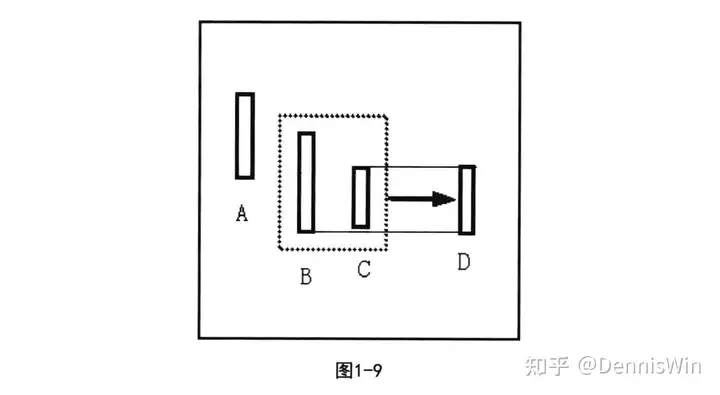
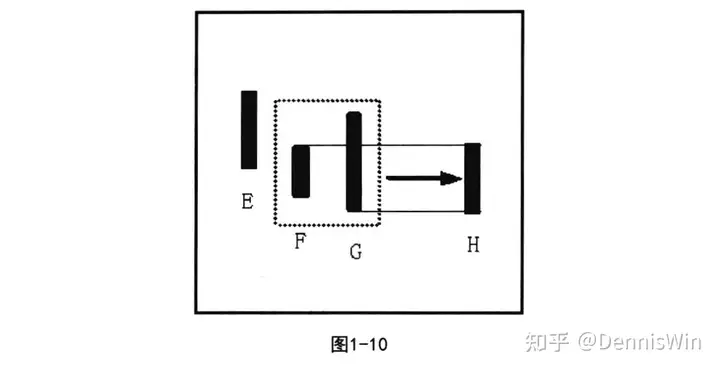
如图1-10所示，FG向下处理，取两根K线中最低点为低点，较高点为高点，合并成新K线H。

3. K线包含处理的顺序

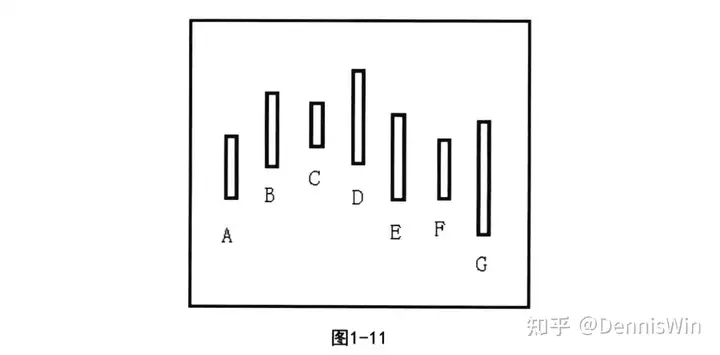
进行K线包含处理时，必须按照时间的先后顺序来进行，即先合并前面的，再依次合并后面的，否则就可能发生紊乱和错误。如图1-11中，B与C、C与D看上去都是包含关系，但合并处理时，要求按照时间先后顺序来合并B与C 待产生新K线后再与D比较。若仍存在包含关系，再合并处理。若不存在包含关系，则当然不再进行包含处理。E与F、F与G之间同理。

走势图中K线合并的全部演化过程。如图1-12所示，第一步要求合并B与C,因为B的高点比A的高点高, B、C取向上处理，结果产生新K线M。

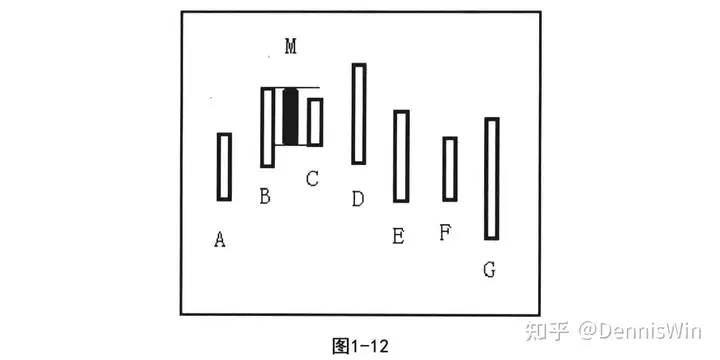
第二步考察新生K线M与K线D之间的关系，发现M与D仍为包含关系则继续合并。此时因M的高点比A的高点高，M、D取向上处理，结果产生新K线N。如图1-13所示。

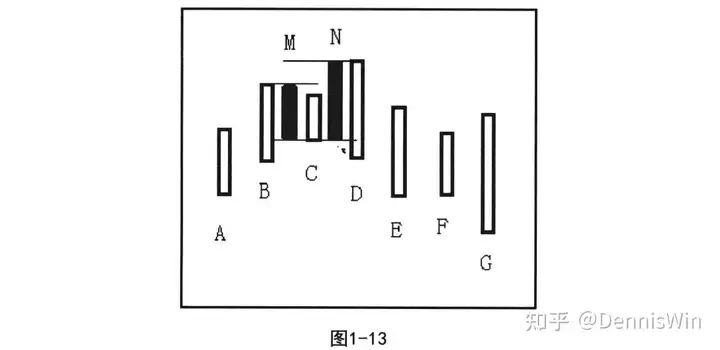
第三步合并E与F，因为E的高点比N的高点低，E、F取向下处理，结果产生新K线0。如图1-14所示。

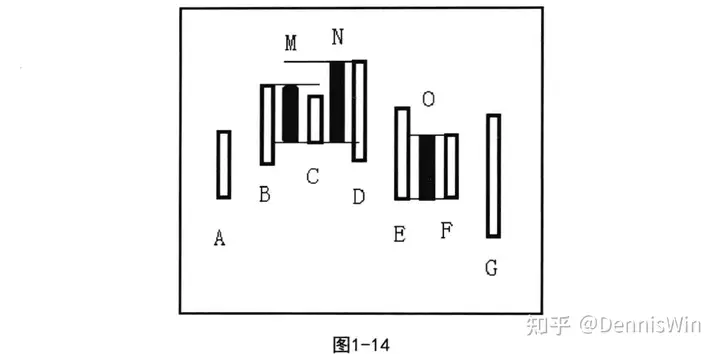
第四步考察新生K线0与K线G之间的关系，发现0与G仍为包含关系， 继续合并。因为0的高点比N的高点低。G取向下处理，结果产生新K线P。如图1-15所示。

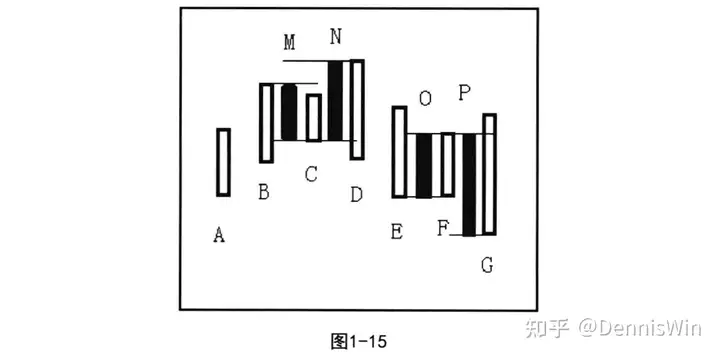
通过合并处理，图1-11中的K线走势就变成A、N、P三条K线。如 图1一16所示。

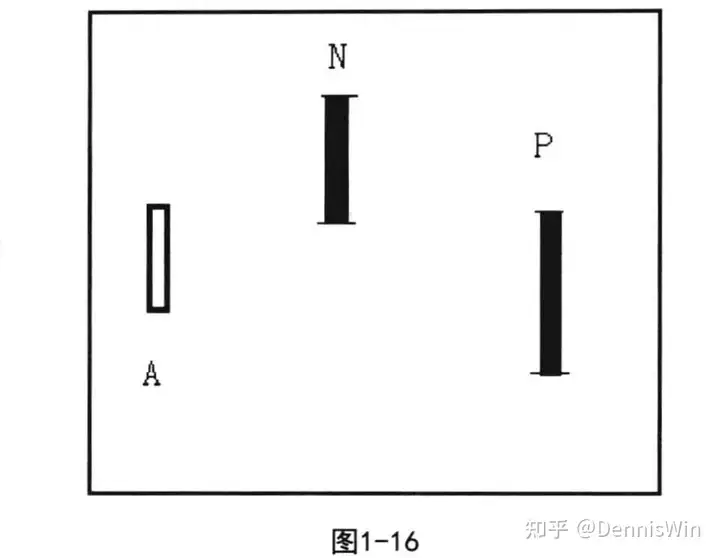
经过彻底合并处理后的K线图中，一定不再存在有包含关系的K线，否则就是合并不彻底，仍有继续合并处理的要求。进行K线处理合并的主要目的是为了识别顶底分型，因此对于K线图中的 某些非关键位置的包含K线，就没有一定合并处理的必要。只要熟练掌握了其方法，K 线合并处理也是一眼就能看出个大概来的， 只要多加练习，即可熟能生巧。