Set Cover问题的贪心近似算法分析

问题描述

全集 \(U = \{ e_1, e_2, ... , e_n \}\) 被划分为一系列的子集 \(S = \{ S_1, S_2, ... , S_k \}\)。且存在一个cost函数\(c: S \rightarrow \mathbb{R}^+\)。

目标是挑选子集使其覆盖所有全集 \(U\) 的元素同时cost最小

问题算法

该问题是经典的NPC问题。

给出其中一种近似算法：贪心策略，近似因子\(\ln n\)。如下描述

在每次迭代选择中，记当前已覆盖元素的集合为\(C\)。我们选择使得 \(\frac{cost(S)}{|S \backslash C|}\) 最小的 \(S\) 作为下一个子集，直至 \(C = U\)

近似因子分析

可以对每个被覆盖的元素定义一个价值函数 \(price\)，$ price(e) = \frac{cost(S)}{|S \backslash C|}$，e是在该次选择 \(S\) 的贪心迭代中被覆盖的。可以清楚的感知到我们希望元素的price尽可能小，且最终的 $ 总cost = \sum\limits_{k=1}^{n} price(e_k) $

不妨按\(e_i\)被覆盖的顺序重新排列 \(U\) 中的元素为 \(\{ e_1, e_2, ..., e_k, ... , e_n \}\)。不失一般性，讨论任意某次迭代：在迭代之初，\(e_k\)尚未被覆盖，但根据算法将在此次迭代中将被选中的 \(S_i\) 覆盖。记原问题的最佳覆盖选择为\(OPT\)，对于剩余元素的最佳覆盖选择为\(OPT_{剩余}\)，有：

• 剩余元素数量 $ |U \backslash C| \geq n-k+1 $
• 此次贪心迭代所选集合的元素price 必不大于 剩余元素的最佳覆盖选择的平均元素price （局部贪心肯定最小）
• 剩余元素的最佳覆盖cost 必不大于 所有元素的最佳覆盖cost （都是最优解）

\[ price(e_k) = \frac{cost(S_i)}{|S_i \backslash C|} \leq \frac{cost(OPT_{剩余})}{|U \backslash C|} \leq \frac{cost(OPT)}{|U \backslash C|} \leq \frac{cost(OPT)}{n-k+1}
\]

所以有

\[ total\ cost = \sum\limits_{k=1}^{n} price(e_k) \leq (1 + \frac{1}{2} + \frac{1}{3} + ... + \frac{1}{n}) \cdot cost(OPT) = H_n \cdot cost(OPT) \leq \ln n \cdot cost(OPT)
\]

即 $ \delta = \ln n $

紧致性证明

构造情况如下

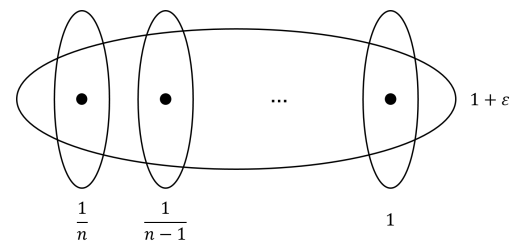
OPT为选择一个 \(1+\epsilon\) 的集合；贪心算法为选择剩下的所有集合。随着\(\epsilon \rightarrow 0\)，近似因子趋近于调和级数 \(H_n\)