[学习笔记]最近公共祖先(LCA)之倍增算法

1.定义

倍增法，顾名思义就是翻倍。它能够大大地优化时间复杂度。这个方法在很多算法中均有应用,例如求 LCA（最近公共祖先）。(大雾)

2.框架

如下图，我们想找 \(4\) 和 \(8\) 的最近公共祖先，该怎么做呢？



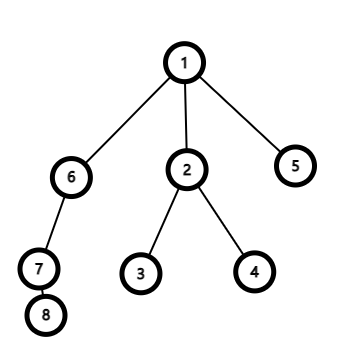
以人类智慧来解决，当然就是一眼看出来，他们两个的最大公共祖先是根节点，如图：



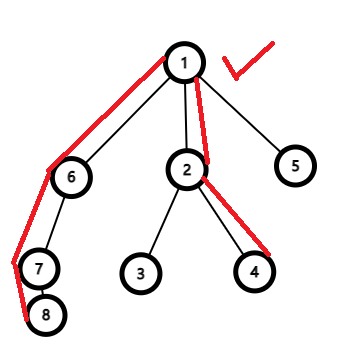
但计算机可不知道这些，所以倍增算法应运而生

他的思路是什么呢？还如图为例。

我们先让两个查询节点位于同一层上，如图



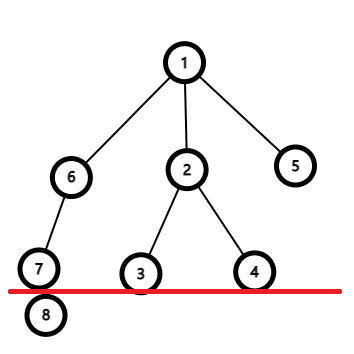
改变后为



（\(7\) 为 \(8\)）

好的，然后我们让两个节点分别向上“跳”，如图



因为下面的节点没什么用，所以我在图片中删除，但在运行过程中并不是。

继续向上跳



这是我们发现，两个点出现在一起，所以 \(1\) 就是他们的最大公共祖先。

3.代码

int get_depth(int node,int father)//当前点和父亲
{
	depth[node]=depth[father]+1;
	fa[node][0]=father;
	for(int i=1;i<=lg2[depth[node]]-1;i++)
		fa[node][i]=fa[fa[node][i-1]][i-1];//node的2^i级父亲等于它的  2^(i-1)级父亲的2^(i-1)级父亲
	for(int i=head[node];i;i=tree[i].next)
		if(tree[i].to!=father) get_depth(tree[i].to,node);
}

inline int LCA(int x,int y)
{
	if(depth[x]<depth[y])
		temp=x,x=y,y=temp;//确保x更深，便于处理
	while(depth[x]>depth[y])
		x=fa[x][lg2[depth[x]-depth[y]]-1];//跳到相同高度
	if(x==y) return x;
	for(int i=lg2[depth[x]]-1;i>=0;i--)
		if(fa[x][i]!=fa[y][i])
			x=fa[x][i],y=fa[y][i];
	return fa[x][0];//注意返回的不是x，是x的父亲
}

完结散花 ⎛⎝≥⏝⏝≤⎛⎝