B树与B+详解
承接上篇SQLite采用B树结构使得SQLite内存占用资源较少，本篇将讲述B树的具体操作（建树，插入，删除等操作）。在看博客时，建议拿支笔和纸，一点一点操作，毕竟知识是自己的，自己也要消化的。本篇通读下来，大约需要25-35分钟，关键掌握B树的具体操作思想，欢迎大家指正。
一、前言
动态查找树主要包括：二叉查找树，平衡二叉树，红黑树，B树，B-树，查找的时间复杂度就为O(log2N)，通过对数就可以发现降低树的深度就会提高查找效率。在大数据存储过程，大量的数据会存储到外存磁盘，外存磁盘中读取与写入某数据的时候，首先定位到磁盘中的某一块，这就有个问题：如何才能有效的查找磁盘中的数据呢，这就需要一种高效的外存数据结构，也就引出了下面的课题。
B树为了存储设备或者磁盘而设计的一种平衡查找树，与红黑树类似（拓展会讲）。
拓展：
B树与红黑树的
不同在于：B树的节点可以有很多子女，从几个到几万个不等，
相同：一颗含有n个节点的B树高度和红黑树是一样的，都是O（lgn）。
二、定义
1.B树
（1）一棵m阶的B树，特性如下：
利用书面的定义（参考书籍-《数据结构》）
1）树中的每个结点最多含有m个孩子；
2）除了根结点和叶子结点，其他结点至少有[ceil(m / 2)（代表是取上限的函数）]个孩子；
3）若根结点不是叶子结点时，则至少有两个孩子（除了没有孩子的根结点）
4）所有的叶子结点都出现在同一层中，叶子结点不包含任何关键字信息；
（2）B树的类型与节点定义
#define m 1024
struct BTNode;
typedef struct BTNode *PBTNode;
struct BTNode {
int keyNum;//实际关键字个数，keyNum < m
PBTNode parent;//指向父亲节点
PBTNode *ptr;
keyType *key;//关键字向量 } typedef struct BTNode *BTree;
typedef BTree *PBTree;
2.B+树
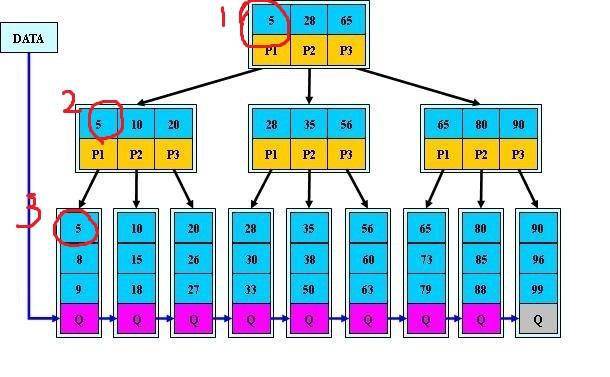
B+树可以说是B树的一种变形，它把数据都存储在叶结点，而内部结点只存关键字和孩子指针，因此简化了内部结点的分支因子，B+树遍历也更高效，其中B+树只需所有叶子节点串成链表这样就可以从头到尾遍历，其中内部结点是并不存储信息，而是存储叶子结点的最小值作为索引，下面将讲述到。
定义：参考数据《数据结构》与百度百科
B+树用于数据库和文件系统中，NTFS等都使用B+树作为数据索引，
1）有n棵子树的结点含有n个关键字，每个关键字都不会保存数据，只会用来索引，并且所有数据都会保存在叶子结点；
2）所有的叶子结点包含所有关键字信息以及指向关键字记录的指针，关键字自小到大顺序连接；
参考下图（来自百度百科）
三、问答
1.为什么说B+树比B树更适合做操作系统的数据库索引和文件索引？
（1）B+树的磁盘读写的代价更低
B+树内部结点没有指向关键字具体信息的指针，这样内部结点相对B树更小。
（2）B+树的查询更加的稳定
因为非终端结点并不是最终指向文件内容的结点，仅仅是作为叶子结点中关键字的索引。这样所有的关键字的查找都会走一条从根结点到叶子结点的路径。所有的关键字查询长度都是相同的，查询效率相当。
四、B树与B+树操作（建议大家找张纸，跟着一起，毕竟知识是自己的）
1.B树
1.1 B树的插入
B树的插入是指插入一条记录，如果B树已存在需要插入的键值时，用新的值替换旧的值；若B树不存在这个值时，则是在叶子结点进行插入操作。
对高度为h的m阶B树，新结点一般插第h层。通过检索可以确定关键码应插入的位置，
1）若该结点中关键码个数小于等于m-1，则直接插入就可
2）若该结点中关键码个数等于m-1，则将引起结点的分裂，以中间的关键码为界将结点一分为二，产生了一个新的结点，并将中间关键码插入到父结点中；
重复上述过程，最坏情况一直分裂到根结点， 建立一个新的根结点，整个B树就增加一层。
举例如下：
》〉》〉下面以5阶B树举例，根据B树的定义，结点最多有4个值，最少有2个值。
a）在空树插入39，此时就有一个值，根结点也是叶子结点
b）继续插入22，97和41值，根结点变为4个值，符合要求
c）插入53值
插入之后发现超过结点最多只有4个值，所以要以中间值进行分开，分开后当前结点要指向父结点，分裂之后，发现符合要求
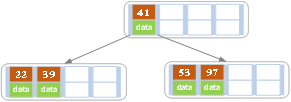
d）插入13，21，40，同样造成分裂，
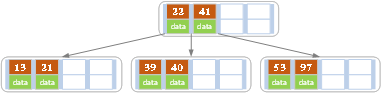
e）紧接着插入30，27，33，36，24，34，35
f）将26再次插入进去
发现有5个值，超过B树的定义，需要以27为中心分裂，27进军父结点
发现父结点也超过4个，再次分裂
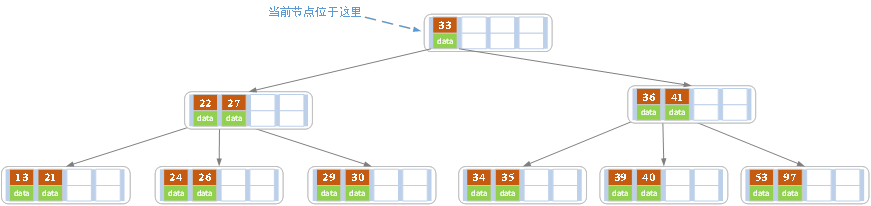
g）最后插入17，28，29，31，32的记录
1.2 B树的删除
B树删除：首先要查找该值是否在B树中存在，如果存在，判断该元素是否存在左右孩子结点，如果有，则上移孩子结点中的相近结点（左孩子最右边的结点或者有孩子最左边的结点）到父结点中，然后根据移动之后的情况；如果没有，进行直接删除；如果不存在对应的值，则删除失败。
1）如果当前要删除的值位于非叶子结点，则用后继值覆盖要删除的值，再用后继值所在的分支删除该后继值。（该后继值必须位于叶子结点上）
2）该结点值个数不小于Math.ceil(m/2)-1（取上线函数），结束删除操作，否则下一步
3）如果兄弟结点值个数大于Math.ceil(m/2)-1，则父结点中下移到该结点，兄弟的一个值上移，删除操作结束。
将父结点的key下移与当前的结点和他的兄弟姐妹结点key合并，形成一个新的结点，
有些结点可能有左兄弟，也有右兄弟，我们可以任意选择一个兄弟结点即可。
》〉》〉下面以5阶B树举例进行删除，根据B树的定义，结点最多有4个值，最少有2个值。
a）原始状态
b）在上面的B树删除21，删除之后结点个数大于等于2，所以删除结束
c）删除27之后为
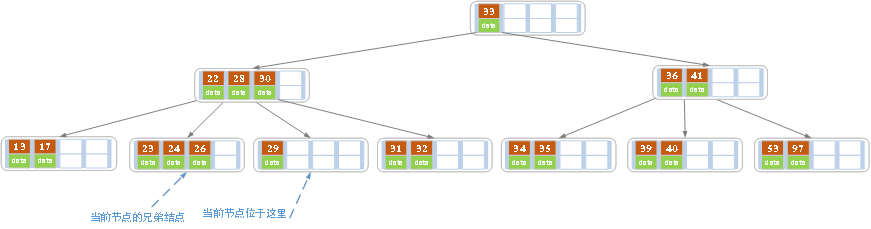
27处于非叶子结点，用27的后继替换。也即是28替换27，然后在右孩子结点删除28，如上。
发现删除，当前叶子结点的记录的个数已经小于2，而兄弟结点中有3个记录我们可以从兄弟结点中借取一个key，父结点中的28就下移，兄弟结点中的26就上移,删除结束，结果如下
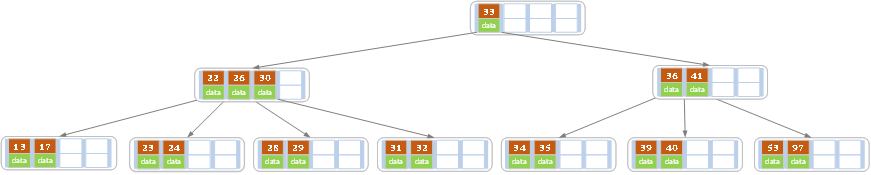
d）删除32
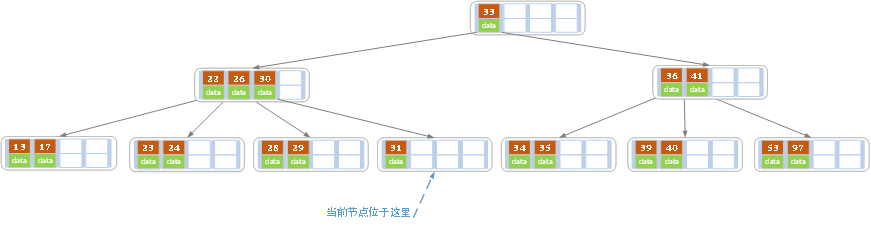
删除之后发现，当前结点中有key，而兄弟都有两个key，所以只能让父结点的30下移到和孩子一起合并，成为新的结点，并指向父结点，经拆封发现符合要求
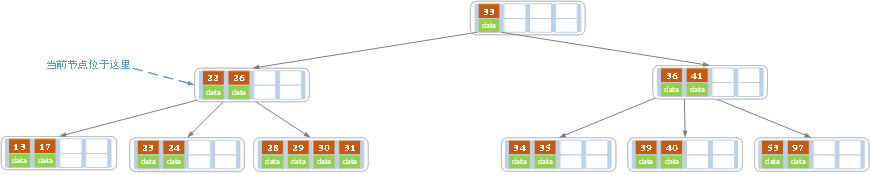
2.B+树
2.1 B+树的插入
B+树插入：
1）若为空树，直接插入，此时也就是根结点
2）对于叶子结点：根据key找叶子结点，对叶子结点进行插入操作。插入后，如果当前结点key的个数不大于m-1，则插入就结束。反之将这个叶子结点分成左右两个叶子结点进行操作，左叶子结点包含了前m/2个记录，右结点包含剩下的记录key，将第m/2+1个记录的key进位到父结点中（父结点必须是索引类型结点），进位到父结点中的key左孩子指针向左结点,右孩子指针向右结点。
3）针对索引结点：如果当前结点key的个数小于等于m-1，插入结束。反之将这个索引类型结点分成两个索引结点，左索引结点包含前(m-1)/2个数据，右结点包含m-(m-1)/2个数据，然后将第m/2个key父结点中，进位到父结点的key左孩子指向左结点, 父结点的key右孩子指向右结点。
》〉》〉下面以5阶B+树举例进行插入，根据B+树的定义，结点最多有4个值，最少有2个值。
a）空树插入5，8，10，15
b）插入16
超过了最大值4，所以分裂，以中间为准
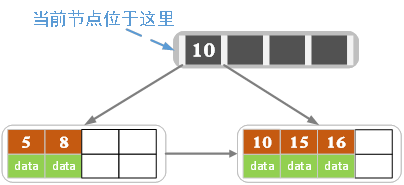
c）插入17，18
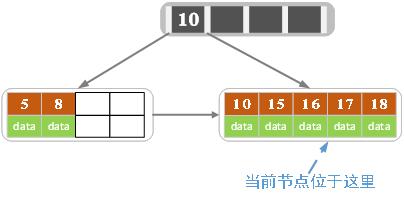
结点的关键字等于5，大于4，进行分裂。
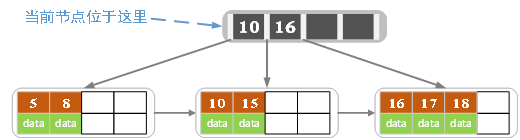
符合条件，插入完成。
2.2 B+树删除
》〉》〉下面以5阶B+树举例进行删除，根据B+树的定义，结点最多有4个值，最少有2个值。
下面是初始状态
a）删除22，删除后个数为2，删除结束
b）删除15，结果如下：
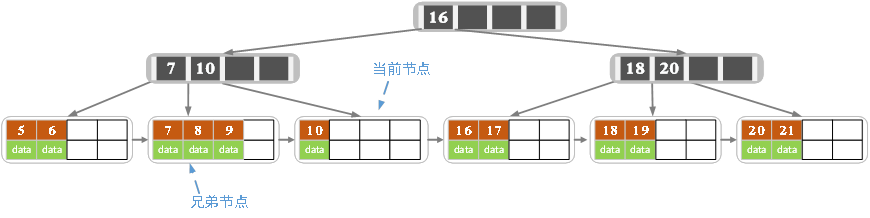
删除之后，只有一个值，而兄弟有三个值，所以从兄弟结点借一个关键字，并更新索引结点
大家可以考虑删除7.我在这里直接给出结果
以上就是B树和B+树的操作，建议大家拿支笔操作一下，毕竟提高能力是没有错的。
五、代码实现
//测试程序1
#include <iostream>
#include <cstdlib>
#include <ctime>
#include "BTree.h"
using namespace std; int main()
{
char iKey[] = {'C','N','G','A','H','E','K','Q','M','F','W','L','T','Z','D','P','R','X','Y','S'};
char dKey[] = {'C','N','G','A','H','E','K','Q','M','F','W','L','T','Z','D','P','R','X','Y','S'};
int iSize = sizeof(iKey)/sizeof(char);
int dSize = sizeof(dKey)/sizeof(char); int i;
BTree<char> btree(, NULL);
cout<<"----------插入测试----------"<<endl;
for(i = ; i < iSize; i++) //插入测试
{
cout<<"插入"<<iKey[i]<<"以后"<<endl;
btree.Insert(iKey[i]);
btree.PrintBTree();
}
cout<<"----------删除测试----------"<<endl;
for(i = ; i < dSize; i++) //删除测试
{
cout<<"删除"<<dKey[i]<<"以后"<<endl;
btree.Delete(dKey[i]);
btree.PrintBTree();
}
return ;
}
//测试程序2
#include <iostream>
#include <cstdlib>
#include <ctime>
#include "BTree.h"
using namespace std; int main()
{
srand((int)time());
const int iSize = ; //插入次数
const int dSize = ; //删除次数
const int num = ; //测试组数
int *iKey = new int[iSize];
int *dKey = new int[dSize];
int i, j;
for(j = ; j < num; j++) //测试组数，每次测试都是插入iSize次，删除dSize次
{
for(i = ; i < iSize; i++) //插入数据生成
iKey[i] = rand()%iSize;
for(i = ; i < dSize; i++)
dKey[i] = rand()%iSize; //删除数据生成 int m = rand()% + ; //随机生成3阶到402阶
BTree<int> btree(m, NULL);
cout<<"----------第"<<j<<"组插入测试----------"<<endl;
for(i = ; i < iSize; i++) //插入测试
btree.Insert(iKey[i]);
cout<<"第"<<j<<"组插入测试成功，为"<<m<<"阶B树"<<endl;
cout<<"----------第"<<j<<"组删除测试----------"<<endl;
for(i = ; i < dSize; i++) //删除测试
btree.Delete(dKey[i]);
cout<<"第"<<j<<"组删除测试成功，为"<<m<<"阶B树"<<endl<<endl;
}
delete [] iKey;
delete [] dKey;
return ;
}
//BTree.h文件，由于使用了模板所以没法将声明与实现分离
#pragma once
#include <queue>
using namespace std; //B树的结点定义
template <typename T>
struct BTreeNode
{
int num; //关键字个数
T *K; //指向关键字数组
BTreeNode<T> *parent; //指向父亲结点
BTreeNode<T> **A; //指向孩子结点数组的指针
BTreeNode(int n, int m, BTreeNode<T> *p)
{
num = n;
parent = p;
K = new T[m+]; //最多有m-1个关键字，K0不用，Km用来当哨兵
A = new BTreeNode *[m+]; //最多有m个分支，Am用来当哨兵
for(int i = ; i <= m; i++)
A[i] = NULL;
}
~BTreeNode()
{
delete [] K; K = NULL;
delete [] A; A = NULL;
}
}; //搜索结果的三元组定义
template <typename T>
struct Triple
{
BTreeNode<T> * node; //关键字所在结点
int i; //关键字下标位置
bool tag; //搜索是否成功
Triple(BTreeNode<T> *nd, int pos, bool t)
{ node = nd; i = pos; tag = t;}
}; //B树定义
template <typename T>
class BTree
{
public:
BTree();
BTree(int m , BTreeNode<T> * root);
~BTree();
Triple<T> Search(const T& x); //搜索核心函数
bool Insert(const T& x); //插入核心函数
bool Delete(const T& x); //删除核心函数
void InsertKey(BTreeNode<T> *p, T k, BTreeNode<T> *a, int i); //插入一个二元组(K,A)
void SpliteNode(BTreeNode<T> *p, T *k, BTreeNode<T> **a, int i); //分裂结点
void RightAdjust(BTreeNode<T> *p, BTreeNode<T> *q, int i); //从右子女取关键字
void LeftAdjust(BTreeNode<T> *p, BTreeNode<T> *q, int i); //从左子女取关键字
void LeftCompress(BTreeNode<T> *p, int i); //往左移动1个位置
void RightCompress(BTreeNode<T> *p, int i); //往右移动1个位置
void MergeNode(BTreeNode<T> *p, BTreeNode<T> *q, BTreeNode<T> *pR, int i); //合并两个结点
void PrintBTree(); //打印B树
private:
int m_m; //路数，即最大子树棵数
BTreeNode<T> *m_pRoot; //B树的根结点
};
template<typename T>
BTree<T>::BTree() //默认构造函数
{
m_m = ; //默认是5阶
m_pRoot = NULL; //根结点初始为空
}
template<typename T>
BTree<T>::BTree(int m , BTreeNode<T> * root)
{
m_m = m;
m_pRoot = root;
}
template<typename T>
BTree<T>::~BTree() //释放所有的空间
{
if(m_pRoot != NULL)
{
queue<BTreeNode<T> *> nodeQueue; //利用队列，按层次遍历B树
nodeQueue.push(m_pRoot); //放入根结点
while(nodeQueue.size())
{
BTreeNode<T> * p = nodeQueue.front();
if(p->A[] != NULL) //不是叶结点，需考虑子女结点的删除
{
for(int i = ; i <= p->num; i++)
nodeQueue.push(p->A[i]);
}
nodeQueue.pop();
delete p;
p = NULL;
}
}
}
//函数功能： 查找关键字x是否在B树中
//函数参数： x为查找的关键字
//返回值： 一个Triple对象(node, i, tag)，tag=true表示x等于结点r中的Ki；tag=false表示x不在树中，r是最后一个被搜索的结点
template <typename T>
Triple<T> BTree<T>::Search(const T &x)
{
int i = ; //下标
BTreeNode<T> *p = m_pRoot, *q = NULL; //用来保存当前结点和它的父结点 while(p != NULL) //一直检查到叶结点
{
//n, A0,(K1, A1), (K2, A2), ... (Kn, An)
//确定i，使得Ki <= x < Ki+1，K[0]不放数据
//下面这条语句当然也可以写成 for(i = 1; i <= n && x >= p->K[i]; i++)
//但是为了与Ki <= x < Ki+1这个关系式统一，采用了下述写法，观察后面的程序，发现这样写还避免了下标溢出的判断
int n = p->num; //当前结点的关键字个数
for(i = ; i < n && x >= p->K[i+]; i++) //可以改进一下，用二分查找
;
if(x == p->K[i]) //是否已找到，不用判断下标，i最大为n
return Triple<T>(p, i, true);
q = p;
p = p->A[i]; //搜索下一层，Ki与Ki+1中间的指针
}
return Triple<T>(q, i, false); //x不在树中，找到了可以插入的结点位置
}
//函数功能： 插入关键字x到B树中
//函数参数： x为插入的关键字
//返回值： 插入是否成功
template <typename T>
bool BTree<T>::Insert(const T &x)
{
if(m_pRoot == NULL) //空树
{
m_pRoot = new BTreeNode<T>(, m_m, NULL); //新的根含有1个关键字
m_pRoot->K[] = x; //根的关键字
return true;
} Triple<T> triple = Search(x); //检查是否已存在
if(triple.tag == true) //x已在B树中
return false; BTreeNode<T> *p = triple.node, *q; //结点地址
//构造插入的两元组(k,a) 其中k为关键字，a为右邻指针
BTreeNode<T> *a = NULL;
T k = x;
int i = triple.i; while() //插入过程
{
if(p->num < m_m-) //关键字个数未到达上限，可以直接插入
{
InsertKey(p, k, a, i); //(k, a)插入到位置(Ki, Ai)后面
return true;
}
SpliteNode(p, &k, &a, i); //将p结点分裂成两个结点，一个结点仍为p，另外一个变为两元组(k,a)，以便插入到父结点
if(p->parent != NULL) //父结点不为空
{
q = p->parent; //获得父结点
for(i = ; i < q->num && x >= q->K[i+]; i++) //确定新的插入位置i
;
p = q; //进入上一层
}
else
{
//已经到达了根，需要新建一个结点
m_pRoot = new BTreeNode<T>(, m_m, NULL); //新的根含有1个关键字
m_pRoot->K[] = k; //新根的关键字
m_pRoot->A[] = p; //左指针
m_pRoot->A[] = a; //右指针
p->parent = a->parent = m_pRoot; //更新左右指针的父结点
return true;
}
}
}
//函数功能： 插入关键字x到B树中，这是实际的插入函数
//函数参数： p指向插入关键字所在结点，k为插入的关键字，a为关键字的右邻，i为插入位置
//返回值： 无
template <typename T>
void BTree<T>::InsertKey(BTreeNode<T> *p, T k, BTreeNode<T> *a, int i)
{
for(int j = p->num; j > i; j--) //将K[i],A[i]以后的元素都往后移一个位置
{
p->K[j + ] = p->K[j];
p->A[j + ] = p->A[j];
}
p->num++; //结点的关键字个数加1
p->K[i + ] = k; //插入两元组在K[i],A[i]以后
p->A[i + ] = a;
if(a != NULL) //若为为空，需更新父结点指针
a->parent = p;
}
//函数功能： 分裂结点
//函数参数： p指向要分裂的结点，k指向插入的关键字，a指向关键字的右邻，i为插入位置
//返回值： 无
template <typename T>
void BTree<T>::SpliteNode(BTreeNode<T> *p, T *k, BTreeNode<T> **a, int i)
{
InsertKey(p, *k, *a, i); //先插了再说
int mid = (m_m + )/; //[ceil(m/2)]
int size = (m_m & )? mid : mid + ; //奇偶性决定了分裂时拷贝的关键字个数 BTreeNode<T> *q = new BTreeNode<T>(, m_m, p->parent); //新结点
//将p的K[mid+1...m]和A[mid..m]移到q的K[1...mid-1]和A[0...mid-1]
q->A[] = p->A[mid];
for(int j = ; j < size; j++)
{
q->K[j] = p->K[mid + j];
q->A[j] = p->A[mid + j];
}
//修改q中的子女的父结点为q，这里很重要，因为这些子女原来的父结点为p
if(q->A[] != NULL)
{
for(int j = ; j < size; j++)
q->A[j]->parent = q;
}
//更新结点的关键字个数
q->num = m_m - mid; //结点q：m –[ceil(m/2)], A[ceil(m/2)],(K [ceil(m/2)]+1, A [ceil(m/2)]+1), …, (Km, Am)
p->num = mid - ; //结点p：[ceil(m/2)]–1, A0, (K1, A1), (K2,A2), …, (K[ceil(m/2)]–1, A[ceil(m/2)]–1)
//构建新的两元组(k,a)
*k = p->K[mid];
*a = q;
} //函数功能： 删除关键字x
//函数参数： x为要删除的关键字
//返回值： 删除是否成功
template <typename T>
bool BTree<T>::Delete(const T& x)
{
Triple<T> triple = Search(x); //检查是否已存在
if(triple.tag == false) //x不在B树中
return false;
BTreeNode<T> *p = triple.node, *q; //要删除的关键字所在结点
int i = triple.i; if(p->A[i] != NULL) //非叶结点
{
q = p->A[i]; //找右子树的最小关键码
while(q->A[] != NULL)
q = q->A[];
p->K[i] = q->K[]; //用叶结点替换
LeftCompress(q, ); //删除K[1]，其实只是用后面的结点覆盖一下即可
p = q; //转换为叶结点的删除
}
else
LeftCompress(p, i); //叶结点直接删除，其实只是用后面的结点覆盖一下即可 int mid = (m_m + ) / ; //求[ceil(m/2)]
//下面开始调整
while()
{
if(p == m_pRoot || p->num >= mid-) //情形1和情形2
break;
else
{
q = p->parent; //父亲结点
for(i = ; i <= q->num && q->A[i] != p; i++) //找到p在父结点中的位置Ai
;
if(i == ) //p为最左指针
RightAdjust(p, q, i); //结点p、父结点q、p的右兄弟结点进行旋转调整
else
LeftAdjust(p, q, i); //结点p、父结点q、p的左兄弟结点进行旋转调整
p = q; //向上调整
}
}
if(m_pRoot->num == ) //一颗空树
{
p = m_pRoot->A[];
delete m_pRoot;
m_pRoot = p;
if(m_pRoot != NULL)
m_pRoot->parent = NULL;
}
return true;
}
//函数功能： 通过右子女调整，如果右子女有多余结点，从右子女取一个关键字
//函数参数： p指向被删除的关键字所在结点，q指向父结点，i为p在q中的位置
//返回值： 无
template <typename T>
void BTree<T>::RightAdjust(BTreeNode<T> *p, BTreeNode<T> *q, int i)
{
BTreeNode<T> *pR = q->A[i+]; //p的右兄弟
if(pR->num >= (m_m+)/) //情形3，兄弟有足够多的关键字，即至少还有[ceil(m/2)]
{
//调整p
p->num++; //p的关键字个数加1
p->K[p->num] = q->K[i+]; //父结点相应关键码下移
p->A[p->num] = pR->A[]; //右兄弟最左指针移到p的最右
if(p->A[p->num] != NULL)
p->A[p->num]->parent = p; //修改父结点，原来是pR
//调整父结点
q->K[i+] = pR->K[]; //右兄弟的最小关键码上移到父结点
//调整右兄弟
pR->A[] = pR->A[]; //右兄弟剩余关键字与指针前移
LeftCompress(pR, ); //覆盖K[1],A[1]，关键字个数减1，LeftCompress中自动会减1
}
else
MergeNode(p, q, pR, i + );//情形4 (...p Ki+1 pR...)
}
//函数功能： 通过左子女调整，如果左子女有多余结点，从左子女取一个关键字
//函数参数： p指向被删除的关键字所在结点，q指向父结点，i为p在q中的位置
//返回值： 无
template <typename T>
void BTree<T>::LeftAdjust(BTreeNode<T> *p, BTreeNode<T> *q, int i)
{
BTreeNode<T> *pL = q->A[i-]; //p的左兄弟
if(pL->num >= (m_m+)/) //情形3
{
//调整p
RightCompress(p, ); //p的关键字和指针往右移动，空出位置放左子女的关键字，RightCompress会自动加1
p->A[] = p->A[];
p->K[] = q->K[i]; //父结点相应关键码下移
p->A[] = pL->A[pL->num]; //左兄弟最右指针移到p的最左
if(p->A[] != NULL)
p->A[]->parent = p; //修改父结点，原来是pL
//调整父结点
q->K[i] = pL->K[pL->num]; //左兄弟的最大关键码上移到父结点
//调整左兄弟
pL->num--; //左兄弟的关键字个数减1
}
else
{
//左右互换一下，以符合合并函数的参数要求
BTreeNode<T> *pR = p;
p = pL;
MergeNode(p, q, pR, i); //情形4，注意这里i，而不是i+1 (...p Ki pR...)
}
}
//函数功能： 将结点p自i+1开始的关键字和指针往左移动1，原来的K[i],A[i]其实被覆盖掉了
//函数参数： p指向结点，i为被覆盖的位置
//返回值： 无
template <typename T>
void BTree<T>::LeftCompress(BTreeNode<T> *p, int i)
{
int n = p->num; //结点关键字个数
for(int j = i; j < n; j++)
{
p->K[j] = p->K[j + ];
p->A[j] = p->A[j + ];
}
p->num--; //关键字个数减1
}
//函数功能： 将结点p自i开始的关键字和指针往右移动1，原来的K[i],A[i]空出来了
//函数参数： p指向结点，i为空出来的位置，用于放新的关键字
//返回值： 无
template <typename T>
void BTree<T>::RightCompress(BTreeNode<T> *p, int i)
{
for(int j = p->num; j >= i; j--) //K[i],A[i]空出来用以放插入的二元组
{
p->K[j + ] = p->K[j];
p->A[j + ] = p->A[j];
}
p->num++; //关键字个数加1
}
//函数功能： 合并两个结点
//函数参数： p指向结点，q指向父亲，pR指向p的右兄弟，i为(...p,K,pR...)中的K位置
//返回值： 无
template <typename T>
void BTree<T>::MergeNode(BTreeNode<T> *p, BTreeNode<T> *q, BTreeNode<T> *pR, int i)
{
int n = p->num + ; //p结点下一个放关键字的位置
p->K[n] = q->K[i]; //下降父结点的关键字
p->A[n] = pR->A[]; //从右兄弟左移一个指针
for(int j = ; j <= pR->num; j++) //将右兄弟剩余关键字和指针移到p中
{
p->K[n + j] = pR->K[j];
p->A[n + j] = pR->A[j];
}
if(p->A[]) //修改p中的子女的父结点为p，这里很重要，因为这些子女原来的父结点为pR，与分裂相对
{
for(int j = ; j <= pR->num; j++)
p->A[n + j]->parent = p;
}
LeftCompress(q, i); //父结点的关键字个数减1
p->num = p->num + pR->num + ; //合并后关键字的个数
delete pR;
pR = NULL;
}
//函数功能： 打印B树
//函数参数： 无
//返回值： 无
template <typename T>
void BTree<T>::PrintBTree()
{
if(m_pRoot != NULL)
{
queue<BTreeNode<T> *> nodeQueue; //利用队列
nodeQueue.push(m_pRoot); //放入根结点
while(nodeQueue.size())
{
BTreeNode<T> * p = nodeQueue.front();
if(p->A[] != NULL) //非叶结点
{
nodeQueue.push(p->A[]); //将子女结点的指针放入队列中
for(int i = ; i <= p->num; i++)
{
nodeQueue.push(p->A[i]);
cout<<p->K[i]<<' ';
}
}
else
{
for(int i = ; i <= p->num; i++)
cout<<p->K[i]<<' ';
} if(p->parent) //打印父结点的第一个关键字
cout<<"-----First key of their parent:"<<p->parent->K[]<<endl;
else
cout<<endl;
nodeQueue.pop();
}
}
}
可以直接运行，大家可以复制粘贴进行效果查看（算法思想很重要）
上面就是B树和B+树从概念到代码应用，B树从数据库引出的，讲完之后，也会重回数据库。下一篇将继续讲解针对SQLite进行封装的FMDB第三方的讲解并附带项目中实际使用。
欢迎大家指正。
B树与B+详解的更多相关文章
- AVL树平衡旋转详解
AVL树平衡旋转详解 概述 AVL树又叫做平衡二叉树.前言部分我也有说到,AVL树的前提是二叉排序树(BST或叫做二叉查找树).由于在生成BST树的过程中可能会出现线型树结构,比如插入的顺序是:1, ...
- P3384 【模板】树链剖分 题解&&树链剖分详解
题外话: 一道至今为止做题时间最长的题: begin at 8.30A.M 然后求助_yjk dalao后 最后一次搞取模: awsl. 正解开始: 题目链接. 树链剖分,指的是将一棵树通过两次遍历后 ...
- BIT 树状数组 详解 及 例题
(一)树状数组的概念 如果给定一个数组,要你求里面所有数的和,一般都会想到累加.但是当那个数组很大的时候,累加就显得太耗时了,时间复杂度为O(n),并且采用累加的方法还有一个局限,那就是,当修改掉数组 ...
- HBase LSM树存储引擎详解
1.前提 讲LSM树之前,需要提下三种基本的存储引擎,这样才能清楚LSM树的由来: 哈希存储引擎. B树存储引擎. LSM树(Log-Structured Merge Tree)存储引擎. 2. 哈希 ...
- 树链剖分详解（洛谷模板 P3384）
洛谷·[模板]树链剖分 写在前面 首先,在学树链剖分之前最好先把 LCA.树形DP.DFS序 这三个知识点学了 emm还有必备的 链式前向星.线段树 也要先学了. 如果这三个知识点没掌握好的话,树链剖 ...
- C# 表达式树 创建、生成、使用、lambda转成表达式树~表达式树的知识详解
笔者最近学了表达式树这一部分内容,为了加深理解,写文章巩固知识,如有错误,请评论指出~ 表达式树的概念 表达式树的创建有 Lambda法 和 组装法. 学习表达式树需要 委托.Lambda.Func& ...
- HDU 1541.Stars-一维树状数组(详解)
树状数组,学长很早之前讲过,最近才重视起来,enmmmm... 树状数组(Binary Indexed Tree(B.I.T), Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据 ...
- 哈夫曼树C++实现详解
哈夫曼树的介绍 Huffman Tree,中文名是哈夫曼树或霍夫曼树,它是最优二叉树. 定义:给定n个权值作为n个叶子结点,构造一棵二叉树,若树的带权路径长度达到最小,则这棵树被称为哈夫曼树. 这个定 ...
- SVN 树冲突解决详解
https://blog.csdn.net/xgf415/article/details/75196714 SVN 冲突包括 内容冲突:当两名(或更多)开发人员修改了同一个文件中相邻或相同的行时就会发 ...
随机推荐
- 你可能不知道的web api
简介 作为前端工作者,我们的工作与web是分不开的,随着HTML5的日益壮大,浏览器自带的webapi也随着增多.本篇文章主要选取了几个有趣且有用的webapi进行介绍,分别介绍其用法.用处以及浏览器 ...
- SQL给数据编号
方法:ROW_NUMBER() over(order by getdate()) AS num 使用案例 : select * From (select ROW_NUMBER() over(orde ...
- 用python处理csv文件
1.准备csv文件(这里是平安银行的统计表:下载并另存为pingan.csv) >>> from urllib import urlretrieve >>> url ...
- Dubbo 源码分析 - 服务调用过程
注: 本系列文章已捐赠给 Dubbo 社区,你也可以在 Dubbo 官方文档中阅读本系列文章. 1. 简介 在前面的文章中,我们分析了 Dubbo SPI.服务导出与引入.以及集群容错方面的代码.经过 ...
- eclipse的这几个小玩意
scroll lock 滚动锁定 word wrap 自动换行 show console when standard out changes 标准输出更改时显示控制台 show cons ...
- 【mysql注入】mysql注入点的技巧整合利用
[mysql注入]mysql注入点的技巧整合利用 本文转自:i春秋社区 前言: 渗透测试所遇的情况瞬息万变,以不变应万变无谓是经验与技巧的整合 简介: 如下 mysql注入点如果权限较高的话,再知道w ...
- JSTL标签库的基本教程之核心标签库(二)
JSTL标签库的基本教程之核心标签库(二) 核心标签库 标签 描述 <c:out> 用于在JSP中显示数据,就像<%= ... > <c:set> 用于保存数据 & ...
- Javascript高级编程学习笔记（64）—— 事件（8）键盘与文本事件
键盘与文本事件 用户在使用键盘时会触发键盘事件 “DOM2级事件”最初规定了键盘事件,但是最后在定稿时又删除了相应内容 所以键盘事件被放入了DOM3级事件的规范中 总的来说有三个键盘事件: keydo ...
- 微信小程序高级基础
微信小程序高级基础 微信小程序的注册和服务器配置: 小程序是什么呢?小程序是一种不需要下载安装就可以使用的应用,它实现了应用"触手可及"的梦想,用户扫一扫或者搜一下就可以打开应用, ...
- Python学习笔记【第八篇】：Python内置模块
什么时模块 Python中的模块其实就是XXX.py 文件 模块分类 Python内置模块(标准库) 自定义模块 第三方模块 使用方法 import 模块名 form 模块名 import 方法名 说 ...