指定so动态链接库连接器
在学习x86_64汇编时, 发现一旦使用glibc库函数, 如printf时, 一般是需要使用为ld传递命令行参数-lc来动态连接libc.so的,
但是, 生成的可执行文件却无法运行:

气煞我也! 于是吾煞费苦心终于找到了解决办法, 并且记录于此, 终有此文.

当然, 我不知道我使用的linux发行版系统的 ld-linux.so.x 藏匿在何处
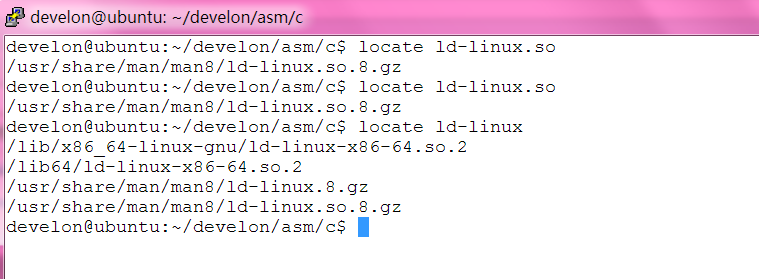
dynamic-linker 救我!

指定so动态链接库连接器的更多相关文章
- Linux下找不到动态链接库
1.生成静态库 生成静态库使用ar工具,其实ar是archive的意思 $ar cqs libhello.a hello.o 2.生成动态库 用gcc来完成,由于可能存在多个版本,因此通常指定版本号: ...
- C++创建动态链接库(*.dll)
1. 从 “文件”菜单中,选择 “新建”,然后选择 “项目…”. 2. 在“项目类型”窗格中,选择“Visual C++”下的“Win32”. 3. 在“模板”窗格中,选 ...
- GCC 编译使用动态链接库和静态链接库的方法
1 库的分类 依据链接时期的不同,库又有静态库和动态库之分. 静态库是在链接阶段被链接的.所以生成的可执行文件就不受库的影响了.即使库被删除了,程序依旧能够成功执行. 有别于静态库,动态库的链接是在程 ...
- Linux下找不到动态链接库(转)
1.生成静态库 生成静态库使用ar工具,其实ar是archive的意思 $ar cqs libhello.a hello.o 2.生成动态库 用gcc来完成,由于可能存在多个版本,因此通常指定版本号: ...
- Linux下找不到动态链接库;
目前,在做的一个程序,编译完后,运行发现报错说找不到自己编译生成的动态库文件,很尴尬;;;果断查资料解决,捎带复制一篇写的比较完善的文章, 地址:http://www.cnblogs.com/wies ...
- gcc动态链接库so的制作和使用
http://blog.csdn.net/CSqingchen/article/details/51546784 参考: http://blog.sina.com.cn/s/blog_69e96b37 ...
- Linux的.a、.so和.o文件 windows下obj,lib,dll,exe的关系 动态库内存管理 动态链接库搜索顺序 符号解析和绑定 strlen函数的汇编实现分析
Linux的.a..so和.o文件 - chlele0105的专栏 - CSDN博客 https://blog.csdn.net/chlele0105/article/details/23691147 ...
- linux动态链接库和静态链接库
Linux下静态链接库与动态链接库的区别 引言 通常情况下,对函数库的链接是放在编译时期(compile time)完成的.所有相关的对象文件 (object file)与牵涉到的函数库(librar ...
- C/C++ 静态链接库(.a) 与 动态链接库(.so)
平时我们写程序都必须 include 很多头文件,因为可以避免重复造轮子,软件大厦可不是单靠一个人就能完成的.但是你是否知道引用的那些头文件中的函数是怎么被执行的呢?这就要牵扯到链接库了! 库有两种, ...
随机推荐
- 如何改变Android标准键的颜色?
本文选自StackOverflow(简称:SOF)精选问答汇总系列文章之一,本系列文章将为读者分享国外最优质的精彩问与答,供读者学习和了解国外最新技术,本文为大家讲解如何改变Android标准键的颜色 ...
- HGOI 20190310 题解
/* 又是又双叒叕WA的一天... 我太弱鸡了... 今天上午打了4道CF */ Problem 1 meaning 给出q组询问,求下列函数的值$ f(a) = \max\limits_{0 < ...
- Codeforces | CF1029D 【Concatenated Multiples】
\(qwq\)昨天晚上\(Div.3\)过了这道题...早上交了\(1A\)...看在\(CF\)上\(hack\)的情况并不乐观而且也没人来交这题的份上...我决定发一篇题解帮\((zhuang)\ ...
- luogu2605 基站选址 (线段树优化dp)
设f[i][j]表示在第i个村庄建第j个基站的花费 那么有$f[i][j]=min\{f[k][j-1]+w[k,i]\}$,其中w[k,i]表示在k,i建基站,k,i中间的不能被满足的村庄的赔偿金之 ...
- Fiddler 安装配置及使用技巧
下载最新版即可: https://www.telerik.com/fiddler pc配置: pc端上的配置较为简单,主要是记录一下遇到的一些bug以及解决方法. options>HTTPS ...
- Android 新架构组件 -- WorkManager
Android WorkManager compile "android.arch.work:work-runtime:1.0.0-alpha02" 继承Worker类并实现doW ...
- 洛谷P3321 序列统计
气死了,FFT了半天发现是NTT... 1004535809 这个东西是NTT模数,原根为3. 题意:给定集合,元素的大小不超过M.用这些元素组成长为n的序列,要求乘积模M为k,求方案数. n < ...
- Autotools知识点
最近研究了下glog使用autotools编译方法的脚本文件,略有所得 configure.ac AC_INIT初始化一些信息 Package Version ReportBug AC_CONFIG_ ...
- terminate called without an active exception异常
在gcc4.4下,采用回调机制写了一个类似std::thread的线程类. 但是使用时却发生了核心已转移的错误. main函数调用的代码大致是 int main(int argc, char *arg ...
- SpringCloud第一弹(入门)
使用IDEA建立SpringBoot多模块工程不爽啊~算了凑合用吧. 第一步.建立一个POM工程 ..Next ..一路next即可,中间啥也不选 第二步.建立Eureka服务器(这个玩意等同于玩Du ...
