[matlab] 23.matlab自带kmeans函数 实现聚类
clc,clear all;
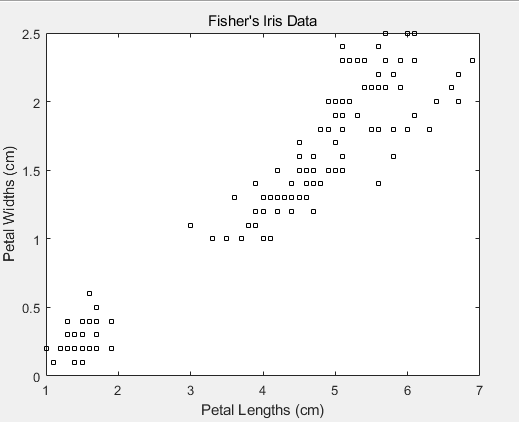
point=[1.40000000000000,0.200000000000000;1.40000000000000,0.200000000000000;1.30000000000000,0.200000000000000;1.50000000000000,0.200000000000000;1.40000000000000,0.200000000000000;1.70000000000000,0.400000000000000;1.40000000000000,0.300000000000000;1.50000000000000,0.200000000000000;1.40000000000000,0.200000000000000;1.50000000000000,0.100000000000000;1.50000000000000,0.200000000000000;1.60000000000000,0.200000000000000;1.40000000000000,0.100000000000000;1.10000000000000,0.100000000000000;1.20000000000000,0.200000000000000;1.50000000000000,0.400000000000000;1.30000000000000,0.400000000000000;1.40000000000000,0.300000000000000;1.70000000000000,0.300000000000000;1.50000000000000,0.300000000000000;1.70000000000000,0.200000000000000;1.50000000000000,0.400000000000000;1,0.200000000000000;1.70000000000000,0.500000000000000;1.90000000000000,0.200000000000000;1.60000000000000,0.200000000000000;1.60000000000000,0.400000000000000;1.50000000000000,0.200000000000000;1.40000000000000,0.200000000000000;1.60000000000000,0.200000000000000;1.60000000000000,0.200000000000000;1.50000000000000,0.400000000000000;1.50000000000000,0.100000000000000;1.40000000000000,0.200000000000000;1.50000000000000,0.200000000000000;1.20000000000000,0.200000000000000;1.30000000000000,0.200000000000000;1.40000000000000,0.100000000000000;1.30000000000000,0.200000000000000;1.50000000000000,0.200000000000000;1.30000000000000,0.300000000000000;1.30000000000000,0.300000000000000;1.30000000000000,0.200000000000000;1.60000000000000,0.600000000000000;1.90000000000000,0.400000000000000;1.40000000000000,0.300000000000000;1.60000000000000,0.200000000000000;1.40000000000000,0.200000000000000;1.50000000000000,0.200000000000000;1.40000000000000,0.200000000000000;4.70000000000000,1.40000000000000;4.50000000000000,1.50000000000000;4.90000000000000,1.50000000000000;4,1.30000000000000;4.60000000000000,1.50000000000000;4.50000000000000,1.30000000000000;4.70000000000000,1.60000000000000;3.30000000000000,1;4.60000000000000,1.30000000000000;3.90000000000000,1.40000000000000;3.50000000000000,1;4.20000000000000,1.50000000000000;4,1;4.70000000000000,1.40000000000000;3.60000000000000,1.30000000000000;4.40000000000000,1.40000000000000;4.50000000000000,1.50000000000000;4.10000000000000,1;4.50000000000000,1.50000000000000;3.90000000000000,1.10000000000000;4.80000000000000,1.80000000000000;4,1.30000000000000;4.90000000000000,1.50000000000000;4.70000000000000,1.20000000000000;4.30000000000000,1.30000000000000;4.40000000000000,1.40000000000000;4.80000000000000,1.40000000000000;5,1.70000000000000;4.50000000000000,1.50000000000000;3.50000000000000,1;3.80000000000000,1.10000000000000;3.70000000000000,1;3.90000000000000,1.20000000000000;5.10000000000000,1.60000000000000;4.50000000000000,1.50000000000000;4.50000000000000,1.60000000000000;4.70000000000000,1.50000000000000;4.40000000000000,1.30000000000000;4.10000000000000,1.30000000000000;4,1.30000000000000;4.40000000000000,1.20000000000000;4.60000000000000,1.40000000000000;4,1.20000000000000;3.30000000000000,1;4.20000000000000,1.30000000000000;4.20000000000000,1.20000000000000;4.20000000000000,1.30000000000000;4.30000000000000,1.30000000000000;3,1.10000000000000;4.10000000000000,1.30000000000000;6,2.50000000000000;5.10000000000000,1.90000000000000;5.90000000000000,2.10000000000000;5.60000000000000,1.80000000000000;5.80000000000000,2.20000000000000;6.60000000000000,2.10000000000000;4.50000000000000,1.70000000000000;6.30000000000000,1.80000000000000;5.80000000000000,1.80000000000000;6.10000000000000,2.50000000000000;5.10000000000000,2;5.30000000000000,1.90000000000000;5.50000000000000,2.10000000000000;5,2;5.10000000000000,2.40000000000000;5.30000000000000,2.30000000000000;5.50000000000000,1.80000000000000;6.70000000000000,2.20000000000000;6.90000000000000,2.30000000000000;5,1.50000000000000;5.70000000000000,2.30000000000000;4.90000000000000,2;6.70000000000000,2;4.90000000000000,1.80000000000000;5.70000000000000,2.10000000000000;6,1.80000000000000;4.80000000000000,1.80000000000000;4.90000000000000,1.80000000000000;5.60000000000000,2.10000000000000;5.80000000000000,1.60000000000000;6.10000000000000,1.90000000000000;6.40000000000000,2;5.60000000000000,2.20000000000000;5.10000000000000,1.50000000000000;5.60000000000000,1.40000000000000;6.10000000000000,2.30000000000000;5.60000000000000,2.40000000000000;5.50000000000000,1.80000000000000;4.80000000000000,1.80000000000000;5.40000000000000,2.10000000000000;5.60000000000000,2.40000000000000;5.10000000000000,2.30000000000000;5.10000000000000,1.90000000000000;5.90000000000000,2.30000000000000;5.70000000000000,2.50000000000000;5.20000000000000,2.30000000000000;5,1.90000000000000;5.20000000000000,2;5.40000000000000,2.30000000000000;5.10000000000000,1.80000000000000]; figure;
plot(point(:,1),point(:,2),'ks','MarkerSize',5);
title 'Fisher''s Iris Data';
xlabel 'Petal Lengths (cm)';
ylabel 'Petal Widths (cm)'; rng(1); % For reproducibility
[idx,C] = kmeans(point,3); x1 = min(point(:,1)):0.01:max(point(:,1));
x2 = min(point(:,2)):0.01:max(point(:,2));
[x1G,x2G] = meshgrid(x1,x2);
XGrid = [x1G(:),x2G(:)]; % Defines a fine grid on the plot idx2Region = kmeans(XGrid,3,'MaxIter',1,'Start',C); figure;
gscatter(XGrid(:,1),XGrid(:,2),idx2Region,[0,0.75,0.75;0.75,0,0.75;0.75,0.75,0],'..');
hold on;
plot(point(:,1),point(:,2),'ks','MarkerSize',5);
title 'Fisher''s Iris Data';
xlabel 'Petal Lengths (cm)';
ylabel 'Petal Widths (cm)';
legend('Region 1','Region 2','Region 3','Data','Location','SouthEast');
hold off;
kmeans
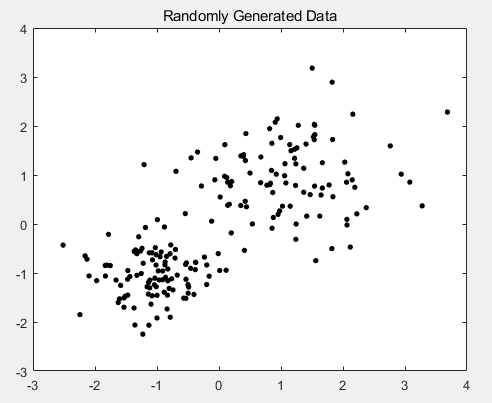
rng default; % For reproducibility
X = [randn(100,2)*0.75+ones(100,2);
randn(100,2)*0.5-ones(100,2)]; figure(1);
plot(X(:,1),X(:,2),'k.','MarkerSize',12);
title 'Randomly Generated Data'; opts = statset('Display','final');
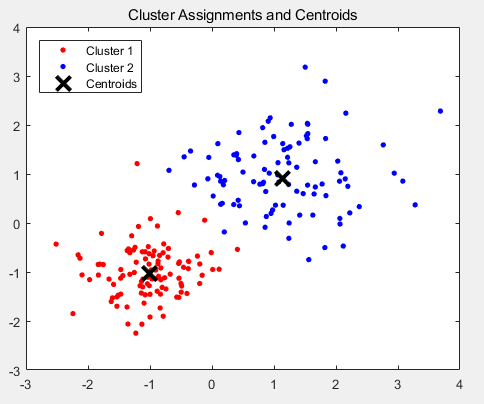
[idx,C] = kmeans(X,2,'Distance','cityblock','Replicates',5,'Options',opts); %这里可以改聚类数量 figure(2);
plot(X(idx==1,1),X(idx==1,2),'r.','MarkerSize',12)
hold on
plot(X(idx==2,1),X(idx==2,2),'b.','MarkerSize',12)
plot(C(:,1),C(:,2),'kx','MarkerSize',15,'LineWidth',3) %标记聚类中心
legend('Cluster 1','Cluster 2','Centroids','Location','NW')
title 'Cluster Assignments and Centroids'
hold off
kmeans
[matlab] 23.matlab自带kmeans函数 实现聚类的更多相关文章
- matlab学习-使用自带的函数
>> %定义矩阵求最大值>> a=[1 7 3;6 2 9];>> A=max(a);>> a a = 1 7 3 6 2 9 >> A A ...
- MATLAB实现最优低通滤波器的函数
MATLAB实现最优低通滤波器的函数 % Fs --Data rate % Fpass --pass band % Fstop --Cutoff frequencies % Apass ...
- 数学建模及机器学习算法（一）：聚类-kmeans（Python及MATLAB实现，包括k值选取与聚类效果评估）
一.聚类的概念 聚类分析是在数据中发现数据对象之间的关系,将数据进行分组,组内的相似性越大,组间的差别越大,则聚类效果越好.我们事先并不知道数据的正确结果(类标),通过聚类算法来发现和挖掘数据本身的结 ...
- [转]matlab语言中的assert断言函数
MATLAB语言没有系统的断言函数,但有错误报告函数 error 和 warning.由于要求对参数的保护,需要对输入参数或处理过程中的一些状态进行判断,判断程序能否/是否需要继续执行.在matlab ...
- 【matlab】MATLAB程序调试方法和过程
3.8 MATLAB程序的调试和优化 在MATLAB的程序调试过程中,不仅要求程序能够满足设计者的设计需求,而且还要求程序调试能够优化程序的性能,这样使得程序调试有时比程序设计更为复杂.MATLAB ...
- Easyui中 alert 带回调函数的 消息框
带回调函数的 消息框: $.messager.alert({ title:'消息', msg:'电话号码 只能是数字!', icon: 'info', width: 300, top:200 , // ...
- 定时器(setTimeout/setInterval)调用带参函数失效解决方法
也许你曾碰到过这样的问题,不管是setInterval()还是setTimeout(),当code参数里放一个带参函数时,定时器都会失效,看下面这个例子: function test(str){ al ...
- 第7.23节 Python使用property函数定义属性简化属性访问的代码实现
第7.23节 Python使用property函数定义属性简化属性访问的代码实现 一. 背景 在本章前面章节中,我们介绍了类相关的知识,并举例进行了说明,在这些例子中会定义一些形如 ...
- Python实现kMeans(k均值聚类)
Python实现kMeans(k均值聚类) 运行环境 Pyhton3 numpy(科学计算包) matplotlib(画图所需,不画图可不必) 计算过程 st=>start: 开始 e=> ...
随机推荐
- js操作css样式，null和undefined的区别？
1.js操作css的样式 div.style.width="100px"在div标签内我们添加了一个style属性,并设定了width值.这种写法会给标签带来大量的style属性, ...
- Netty 系列八（基于 WebSocket 的简单聊天室）.
一.前言 之前写过一篇 Spring 集成 WebSocket 协议的文章 —— Spring消息之WebSocket ,所以对于 WebSocket 协议的介绍就不多说了,可以参考这篇文章.这里只做 ...
- 异常: Recieved SHUTDOWN signal from Resourcemanager ,Registration of NodeManager failed, Message from ResourceManager: NodeManager from localhost doesn't satisfy minimum allocations, Sending SHUTDOWN s
异常: Recieved SHUTDOWN signal from Resourcemanager ,Registration of NodeManager failed, Message from ...
- Http协议请求头、响应头、响应码
Http部分请求头 Accept 客户机通过这个头,告诉服务器,它支持哪些数据类型 Accept-Charset 客户机通过这个头,告诉服务器,它支持的编码 Accept-Encoding 客户机通过 ...
- JavaScript是如何工作的：与WebAssembly比较及其使用场景
摘要: WebAssembly未来可期. 原文:JavaScript是如何工作的:与WebAssembly比较及其使用场景 作者:前端小智 Fundebug经授权转载,版权归原作者所有. 这是专门探索 ...
- 详解javascript事件绑定使用方法
由于html是从上至下加载的,通常我们如果在head部分引入javascript文件,那么我们都会在javascript的开头添加window.onload事件,防止在文档问加载完成时进行DOM操作所 ...
- canvas-a11htmlANDcanvas.html
<!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...
- 洛谷P4589 [TJOI2018]智力竞赛(二分答案 二分图匹配)
题意 题目链接 给出一个带权有向图,选出n + 1n+1条链,问能否全部点覆盖,如果不能,问不能覆盖的点权最小值最大是多少 Sol TJOI怎么净出板子题 二分答案之后直接二分图匹配check一下. ...
- 在“非软件企业”开发软件的困局 ZT
软件产品广泛服务于各行业,其开发具有高科技.高投入.高产出.高风险的特点.在项目开发和软件应用中,只有将人员能力的发挥与科学技术的使用应用市场的认识进行最佳的融合,才能发挥软件的效益.普通企业虽涉足软 ...
- 计算机网络TCP“三次握手”
终于有时间写这篇文章了,最近真的比较忙! TCP协议 之 “三次握手” 引言:我们知道,TCP是面向连接的协议(相较于UDP无连接的协议),会在传送数据之前先在 发送端 & 接收端 之间建立 ...