AT2134 Zigzag MST

题面

题解

这个题目主要是连边很奇怪，但是我们可以发现一个性质：权值是递增的。

于是像下图的连边：（加边方式为\((A_1, B_1, 1)\)）

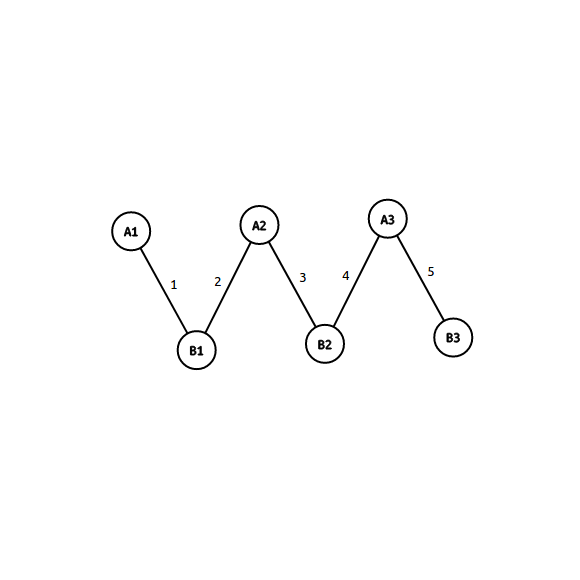
其实可以等价于如下连边：

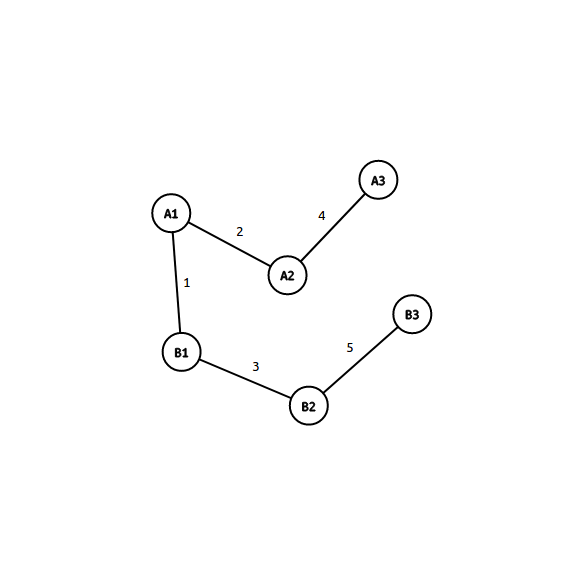
于是我们将其变成了在环上连边。

在环上连边有一点好，就是可以知道边\((i,i+1)\)的边权最小值。

于是将这些边和之前的三元组\((a, b, c)\)放到边集中去，跑kruskal即可。

代码

#include<cstdio>
#include<cstring>
#include<cctype>
#include<algorithm>
#define RG register
#define int long long

inline int read()
{
    int data = 0, w = 1; char ch = getchar();
    while(ch != '-' && (!isdigit(ch))) ch = getchar();
    if(ch == '-') w = -1, ch = getchar();
    while(isdigit(ch)) data = data * 10 + (ch ^ 48), ch = getchar();
    return data * w;
}

const int maxn(2e5 + 10);
struct edge { int x, y, w; } e[maxn << 2];
inline int cmp(const edge &lhs, const edge &rhs) { return lhs.w < rhs.w; }
int dis[maxn], n, Q, e_num, fa[maxn], ans;
int find(int x) { return fa[x] == x ? x : fa[x] = find(fa[x]); }
template<typename T> inline void chkmin(T &x, const T &y) { if(y < x) x = y; }
inline void add_edge(int x, int y, int w) { e[++e_num] = (edge) {x, y, w}; }

signed main()
{
    n = read(), Q = read(); memset(dis, 0x3f, sizeof dis);
    for(RG int i = 1, a, b, c; i <= Q; i++)
        a = read(), b = read(), c = read(),
        add_edge(a, b, c), chkmin(dis[a], c + 1), chkmin(dis[b], c + 2);
    for(RG int i = 0; i < n; i++) chkmin(dis[i], dis[(i - 1 + n) % n] + 2);
    for(RG int i = 0; i < n; i++) chkmin(dis[i], dis[(i - 1 + n) % n] + 2);
    for(RG int i = 0; i < n; i++) add_edge(i, (i + 1) % n, dis[i]), fa[i] = i;
    std::sort(e + 1, e + e_num + 1, cmp);
    for(RG int i = 1; i <= e_num; i++)
    {
        if(find(e[i].x) == find(e[i].y)) continue;
        fa[find(e[i].x)] = find(e[i].y); ans += e[i].w;
    }
    printf("%lld\n", ans);
    return 0;
}