POJ1177（扫描线求周长并）

题意：。。求周长并。。。

解析：参考求面积并

图借鉴自：https://www.cnblogs.com/shuaiwhu/archive/2012/04/22/2464876.html

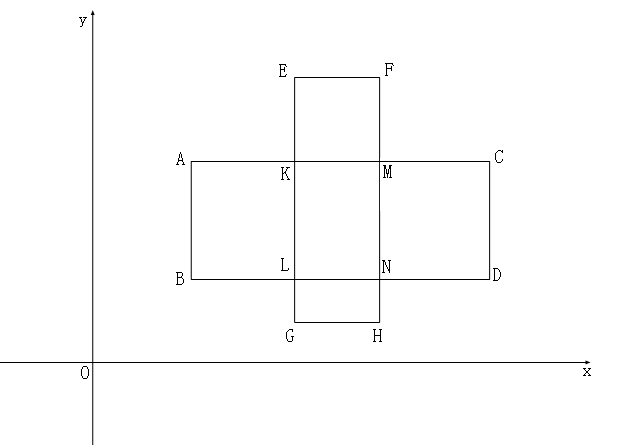
　自下而上扫描 首先 加GH 接着 加 Node[1].numseg * 2 *（Edge[i+1].y - Edge[i].y）即两条竖边   然后 加 BD 但这时要减去GH  因为 LN = GH 重复加了一次

依次推理

与面积并不同的是 最上面的边不要忘了加上。。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cmath>
#define mem(a, b) memset(a, b, sizeof(a))
using namespace std;
const int maxn = , INF = 0x7fffffff;
int X[maxn];

struct node{
    int l, r, w; // l 和 r 分别为线段树的左右端点  w记录边重叠的情况
    int numseg;  // 记录竖边的对数
    int lx, rx, sum;  // sum代表当前区间线段的长度，lx和rx为线段的真实端点
    bool lcover, rcover;  // 标记当前区间的左右端点 与 numseg有关
}Node[maxn*];

struct edge{  // 存边
    int lxx, rxx, y;
    int f;
}Edge[maxn];

int cmp(edge a, edge b)
{
    return a.y < b.y;
}

void build(int k, int ll, int rr)
{
    Node[k].l = ll, Node[k].r = rr;
    Node[k].lx = X[ll];
    Node[k].rx = X[rr];
    Node[k].w = Node[k].numseg = , Node[k].sum = ;
    Node[k].lcover = Node[k].rcover = false;
    if(ll +  == rr) return;
    int m = (ll + rr) / ;
    build(k*, ll, m);
    build(k*+, m, rr);
}

void down(int k)
{
    if(Node[k].w > )
    {
        Node[k].sum = Node[k].rx - Node[k].lx;
        Node[k].numseg = ;
        Node[k].lcover = Node[k].rcover = true;
        return;
    }
    if(Node[k].l +  == Node[k].r)
    {
        Node[k].sum = ;
        Node[k].numseg = ;
        Node[k].lcover = Node[k].rcover = false;
    }
    else
    {
        Node[k].sum = Node[k*].sum + Node[k*+].sum;
        Node[k].lcover = Node[k*].lcover, Node[k].rcover = Node[k*+].rcover;
        Node[k].numseg = Node[k*].numseg + Node[k*+].numseg;
        if(Node[k*].rcover && Node[k*+].lcover) Node[k].numseg--;   //注意这里是左区间的右端点 和 右区间的左端点
    }
}

void update(int k, edge e)
{
    if(Node[k].lx == e.lxx && Node[k].rx == e.rxx)
    {
        Node[k].w += e.f;
        down(k);
        return;
    }
    if(e.rxx <= Node[k*].rx) update(k*, e);
    else if(e.lxx >= Node[k*+].lx) update(k*+, e);
    else
    {
        edge temp = e;
        temp.rxx = Node[k*].rx;
        update(k*, temp);
        temp = e;
        temp.lxx = Node[k*+].lx;
        update(k*+, temp);
    }
    down(k);
}

int main()
{
    int n, cnt = ;
    scanf("%d",&n);
    for(int i=; i<n; i++)
    {
        int x1, x2, y1, y2;
        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
        Edge[++cnt].lxx = x1, Edge[cnt].rxx = x2, Edge[cnt].y = y1, Edge[cnt].f = ;
        X[cnt] = x1;
        Edge[++cnt].lxx = x1, Edge[cnt].rxx = x2, Edge[cnt].y = y2, Edge[cnt].f = -;
        X[cnt] = x2;
    }
    sort(Edge+, Edge+cnt+, cmp);
    sort(X+, X+cnt+);
    int m = unique(X+, X+cnt+) - (X+);
    build(, , m);
    int ret = , last = ;
    for(int i=; i<cnt; i++)
    {
        update(, Edge[i]);
        ret += abs(Node[].sum - last); // 横边
        ret += Node[].numseg *  * (Edge[i+].y - Edge[i].y);  // 加竖边
        last = Node[].sum;
    }
    update(, Edge[cnt]);
    ret += abs(Node[].sum - last);

    printf("%d\n",ret);

    return ;
}