P2057 [SHOI2007]善意的投票 (最大流)

题目

P2057 [SHOI2007]善意的投票

解析

网络流的建模都如此巧妙。

我们把同意的意见看做源点\(s\)，不同意的意见看做汇点\(t\)。

那我们\(s\)连向所有同意的人，\(t\)连向所有反对的人，流量为1，表示了与其原方案直接冲突的代价，好友之间连双向边（双向边使因为可以从同意变为不同意，也可以从不同意变为同意），流量为1，表示改变意见要付出的代价，因为这个人改变意见后，原来与其意见冲突的朋友与他意见就不冲突了，所以代价为1。

我们要让所有人意见统一，就是让源点和汇点之间没有不同的意见，也就是没有连边，所以是求最小割，根据最小割最大流定理，也就是求最大流。

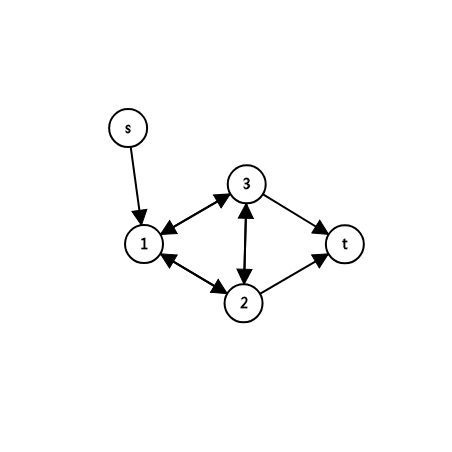
题目中建完图就是这样

代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
const int INF = 0x3f3f3f3f;
int n, m, s, t, num = 1;
int head[N], cur[N], dep[N];
class node {
	public :
		int v, nx, w;
} e[N];

template<class T>inline void read(T &x) {
    x = 0; int f = 0; char ch = getchar();
    while (!isdigit(ch)) f |= (ch == '-'), ch = getchar();
    while (isdigit(ch)) x = x * 10 + ch - '0', ch = getchar();
    x = f ? -x : x;
    return ;
}

inline void add(int u, int v, int w) {
    e[++num].nx = head[u], e[num].v = v, e[num].w = w, head[u] = num;
    e[++num].nx = head[v], e[num].v = u, e[num].w = 0, head[v] = num;
}

queue<int>q;
bool bfs() {
    memset(dep, 0, sizeof dep);
    memcpy(cur, head, sizeof cur);
    dep[s] = 1;
    q.push(s);
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        for (int i = head[u]; ~i; i = e[i].nx) {
            int v = e[i].v;
            if (e[i].w && !dep[v]) dep[v] = dep[u] + 1, q.push(v);
        }
    }
    return dep[t];
}

int dfs(int u, int flow) {
    if (u == t) return flow;
    int use = 0;
    for (int &i = cur[u]; ~i; i = e[i].nx) {
        int v = e[i].v;
        if (e[i].w && dep[v] == dep[u] + 1) {
            int di = dfs(v, min(flow, e[i].w));
            e[i].w -= di, e[i ^ 1].w += di;
            use += di, flow -= di;
            if (flow <= 0) break;
        }
    }
    return use;
}

int dinic() {
    int ans = 0;
    while (bfs()) ans += dfs(s, INF);
    return ans;
}

int main() {
	memset(head, -1, sizeof head);
	read(n), read(m);
	s = n + 1, t = s + 1;
	for (int i = 1, x; i <= n; ++i) {
		read(x);
		if (x) add(s, i, 1);
		else add(i, t, 1);
	}
	for (int i = 1, x, y; i <= m; ++i) {
		read(x), read(y);
		add(x, y, 1);
		add(y, x, 1);
	}
	printf("%d\n", dinic());
}