k8s的chart学习（下）

1.开发自己的chart

Kubernetes 给我们提供了大量官方 chart，不过要部署微服务应用，还是需要开发自己的 chart，下面就来实践这个主题。

1.1创建 chart

执行 helm create mychart 的命令创建 chart mychart：

Helm 会帮我们创建目录 mychart，并生成了各类 chart 文件。这样我们就可以在此基础上开发自己的 chart 了。

新建的 chart 默认包含一个 nginx 应用示例，values.yaml 内容如下：

开发时建议大家参考官方 chart 中的模板、values.yaml、Chart.yaml，里面包含了大量最佳实践和最常用的函数、流控制，这里就不一一展开了。

1.2调试 chart

只要是程序就会有 bug，chart 也不例外。Helm 提供了 debug 的工具：helm lint 和 helm install --dry-run --debug。

helm lint 会检测 chart 的语法，报告错误以及给出建议。

比如我们故意在 values.yaml 的第 10 行漏掉了一个 :，

helm lint mychart 会指出这个语法错误。

将：加上之后再次 helm lint 检查一下， mychart 目录被作为参数传递给 helm lint。错误修复后则能通过检测。

helm install --dry-run --debug 会模拟安装 chart，并输出每个模板生成的 YAML 内容。

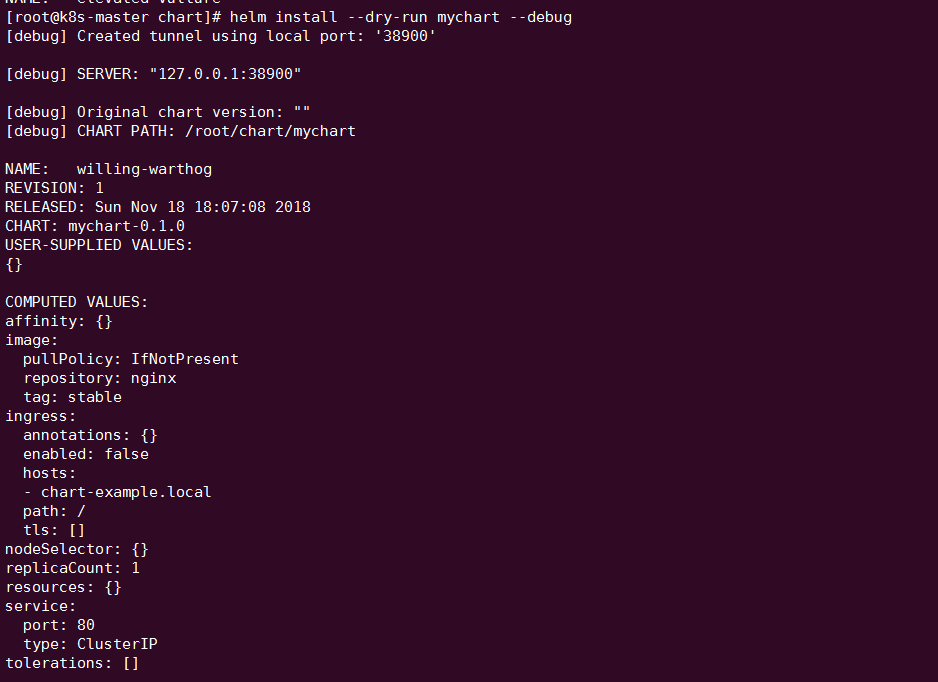
我们可以检视这些输出，判断是否与预期相符。

同样，mychart 目录作为参数传递给 helm install --dry-run --debug。

2.安装 chart的方式

当我们觉得准备就绪，就可以安装 chart，Helm 支持四种安装方法：

2.1安装仓库中的 chart

例如：helm install stable/nginx

2.2通过 tar 包安装

例如：helm install ./nginx-1.2.3.tgz

2.3通过 chart 本地目录安装

例如：helm install ./nginx

2.4通过 URL 安装

例如：helm install https://example.com/charts/nginx-1.2.3.tgz

这里我们使用本地目录安装：

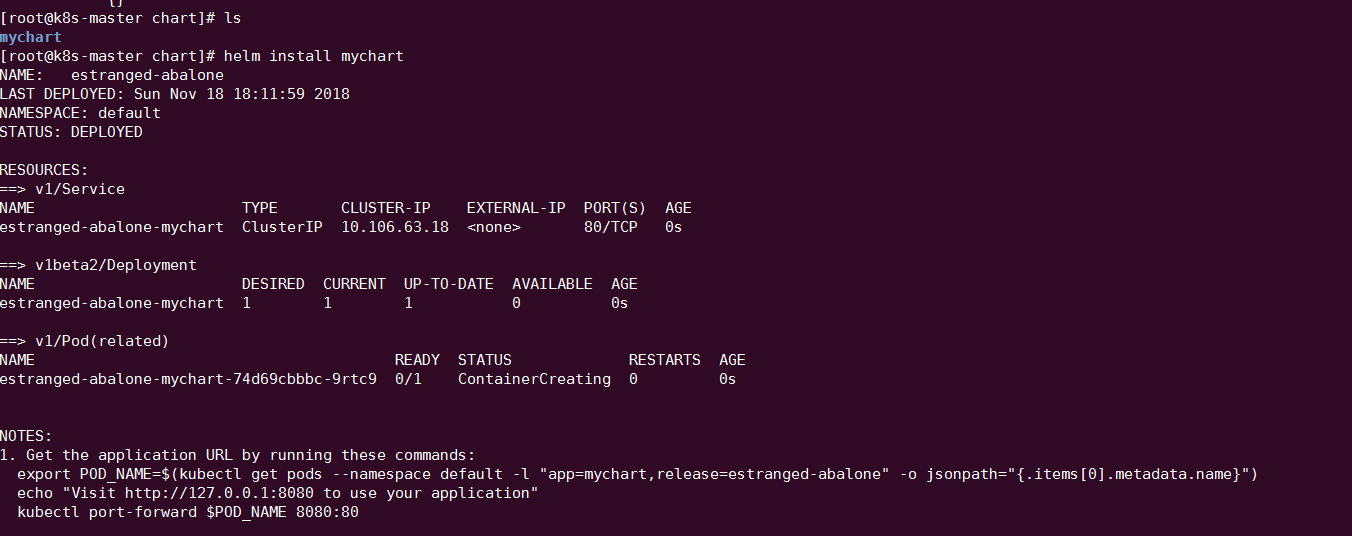
当 chart 部署到 Kubernetes 集群，便可以对其进行更为全面的测试。

3.将 chart 添加到仓库

chart 通过测试后可以将其添加到仓库，团队其他成员就能够使用。任何 HTTP Server 都可以用作 chart 仓库，下面演示在 k8s-node1 10.0.0.12 上搭建仓库。

3.1在 `k8s-node1` 上启动一个 httpd 容器。

3.2通过 `helm package` 将 `mychart` 打包。

3.3执行 `helm repo index` 生成仓库的 index 文件。

mkdir myrepo

cd chart/

helm package mychart

mv chart/mychart-0.1..tgz myrepo/

Helm 会扫描 myrepo 目录中的所有 tgz 包并生成 index.yaml。--url指定的是新仓库的访问路径。新生成的 index.yaml 记录了当前仓库中所有 chart 的信息：

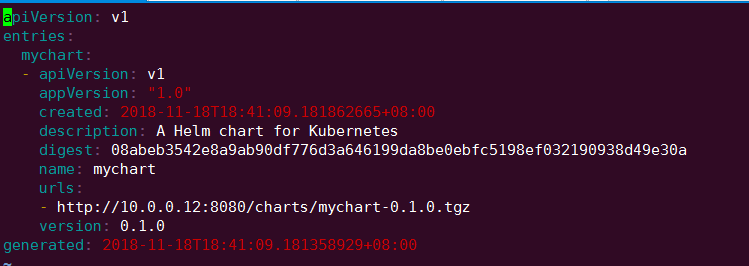
当前只有 mychart 这一个 chart。

3.4将 `mychart-0.1.0.tgz` 和 `index.yaml` 上传到 `k8s-node1` 的 `/var/www/charts` 目录。

3.5通过 `helm repo add` 将新仓库添加到 Helm。

仓库命名为 newrepo，Helm 会从仓库下载 index.yaml。

3.6现在已经可以 `repo search` 到 `mychart` 了。

除了 newrepo/mychart，这里还有一个 local/mychart。这是因为在执行第 2 步打包操作的同时，mychart 也被同步到了 local 的仓库。

3.7已经可以直接从新仓库安装 `mychart` 了。

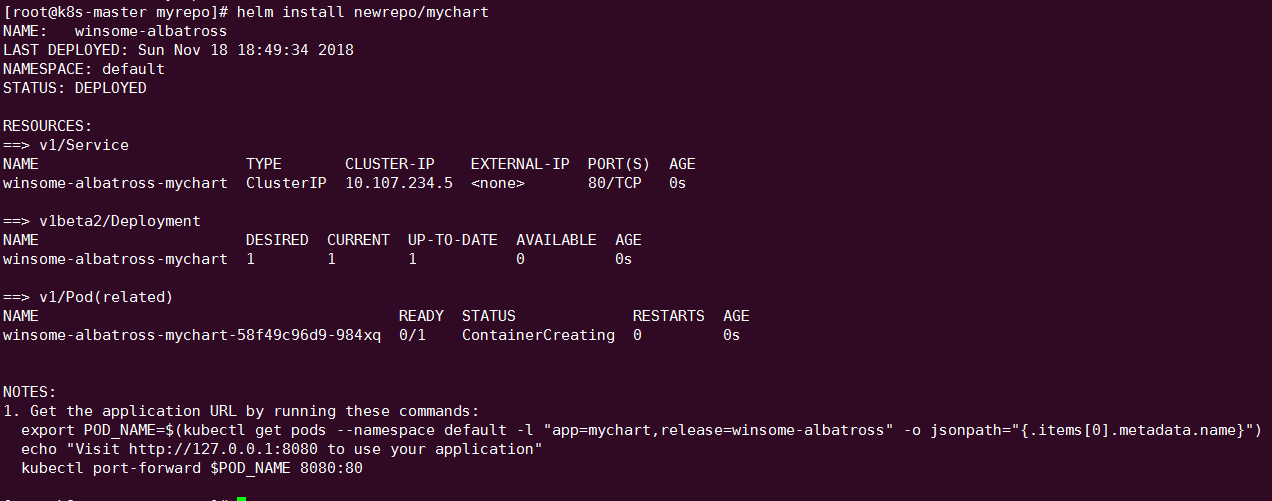
3.8如果以后仓库添加了新的 chart，需要用 `helm repo update` 更新本地的 index。

①是本地仓库默认跳过

②是我们创建的私有仓库能够成功更新

③是阿里的仓库，发现亦可以更新成功

④是google的仓库，国内如果不使用科学上网，是没法访问的，所以更新失败。

4.小结

本章我们学习了 Kubernetes 包管理器 Helm。

Helm 让我们能够像 apt 管理 deb 包那样安装、部署、升级和删除容器化应用。

Helm 由客户端和 Tiller 服务器组成。客户端负责管理 chart，服务器负责管理 release。

chart 是 Helm 的应用打包格式，它由一组文件和目录构成。其中最重要的是模板，模板中定义了 Kubernetes 各类资源的配置信息，Helm 在部署时通过 values.yaml 实例化模板。

Helm 允许用户开发自己的 chart，并为用户提供了调试工具。用户可以搭建自己的 chart 仓库，在团队中共享 chart。

Helm 帮助用户在 Kubernetes 上高效地运行和管理微服务架构应用，Helm 非常重要。