codeforces 703D Mishka and Interesting sum 偶数亦或 离线+前缀树状数组
题目大意:给出n个数字,m次区间询问,每一次区间询问都是询问 l 到 r 之间出现次数为偶数的数 的亦或和。
思路:偶数个相同数字亦或得到0,奇数个亦或得到本身,那么如果把一段区间暴力亦或,得到的其实就是出现次数为奇数的数字的亦或和,所以我们希望这段区间内的所有数字出现次数都+1,使奇偶性互换。
我们先处理出前缀的亦或和,这样可以得到次数为奇数的亦或和。
接下来的问题就是要改变一段区间的奇偶性了,也就是说,这个问题其实就转化成了如何求一段区间出现的所有数字(无重复)。
这里我学到的是用树状数组离线处理的方式。核心代码如下。
for(int i=;i<=m;i++){
while(p<=ask[i].r)
{
if(pos[a[p]]==)//对于每一个第一次出现的数字,加入树状数组,并且记录。
{
pos[a[p]]=p;
update(p,a[p]);
}else
{
update(pos[a[p]],a[p]);//如果曾经出现过,则将之前的位置清空,更新树状数组和记录。
update(p,a[p]);
pos[a[p]]=p;
}
p++;
}
ask[i].ans=pre[ask[i].r]^pre[ask[i].l-]^getxor(ask[i].r)^getxor(ask[i].l-);
}
如此操作后,比如我们询问的是1- R 的区间,此时肯定能得到我要的东西,但是如果我们询问的是1- r 这个区间的话(r<R),这个信息可能就不对了!!但是精彩的地方来了,由于我们事先对询问的区间排过序,也就是说,如果是纯粹的询问1-r区间,这个操作肯定在询问1-R之前,所以不会有影响,而如果我们计算的是r-R这个区间,此时1-r这个东西是出现在 减数 的位置的,也就是说,如果有一个数字在1-r和r-R中间都出现过,则此时1-r的树状数组为0,而1-R的树状数组为1!!
所以根据这个思路把他转化成亦或的求法就可以了。
接下来上代码。
#include<cstdio>
#include<cstring>
#include<stdlib.h>
#include<algorithm>
#include<iostream>
#include<map>
#define CLR(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef long long ll;
const int inf=0x3f3f3f3f;
const int maxn=;
ll pre[maxn],tree[maxn<<],a[maxn];
int n,m;
struct node{
int l,r,id;
ll ans;
}ask[maxn];
bool cmp(const node a,const node b)
{
return a.r<b.r;
}
bool cmpid(const node a,const node b)
{
return a.id<b.id;
}
inline int lowbit(int k){
return (-k)&k;
}
inline void update(int x,ll val){
while(x<=n){
tree[x]^=val;
x+=lowbit(x);
}
}
inline ll getxor(int x){
ll ans=;
while(x>){
ans^=tree[x];
x-=lowbit(x);
}
return ans;
}
map<ll,int >pos;
int main(){
cin>>n;
scanf("%lld",&a[]);
pre[]=a[];
for(int i=;i<=n;i++)
{
scanf("%lld",&a[i]);
pre[i]=pre[i-]^a[i];
}
cin>>m;
for(int i=;i<=m;i++)
{
scanf("%d%d",&ask[i].l,&ask[i].r);
ask[i].id=i;
}
sort(ask+,ask++m,cmp);
int p=;
for(int i=;i<=m;i++){
while(p<=ask[i].r)
{
if(pos[a[p]]==)
{
pos[a[p]]=p;
update(p,a[p]);
}else
{
update(pos[a[p]],a[p]);
update(p,a[p]);
pos[a[p]]=p;
}
p++;
}
ask[i].ans=pre[ask[i].r]^pre[ask[i].l-]^getxor(ask[i].r)^getxor(ask[i].l-);
}
sort(ask+,ask++m,cmpid);
for(int i=;i<=m;i++)
{
printf("%lld\n",ask[i].ans);
}
}
3.5 seconds
256 megabytes
standard input
standard output
Little Mishka enjoys programming. Since her birthday has just passed, her friends decided to present her with array of non-negative integers a1, a2, ..., an of n elements!
Mishka loved the array and she instantly decided to determine its beauty value, but she is too little and can't process large arrays. Right because of that she invited you to visit her and asked you to process m queries.
Each query is processed in the following way:
- Two integers l and r (1 ≤ l ≤ r ≤ n) are specified — bounds of query segment.
- Integers, presented in array segment [l, r] (in sequence of integers al, al + 1, ..., ar) even number of times, are written down.
- XOR-sum of written down integers is calculated, and this value is the answer for a query. Formally, if integers written down in point 2 are x1, x2, ..., xk, then Mishka wants to know the value
 , where
, where  — operator of exclusive bitwise OR.
— operator of exclusive bitwise OR.
Since only the little bears know the definition of array beauty, all you are to do is to answer each of queries presented.
The first line of the input contains single integer n (1 ≤ n ≤ 1 000 000) — the number of elements in the array.
The second line of the input contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109) — array elements.
The third line of the input contains single integer m (1 ≤ m ≤ 1 000 000) — the number of queries.
Each of the next m lines describes corresponding query by a pair of integers l and r (1 ≤ l ≤ r ≤ n) — the bounds of query segment.
Print m non-negative integers — the answers for the queries in the order they appear in the input.
3
3 7 8
1
1 3
0
7
1 2 1 3 3 2 3
5
4 7
4 5
1 3
1 7
1 5
0
3
1
3
2
In the second sample:
There is no integers in the segment of the first query, presented even number of times in the segment — the answer is 0.
In the second query there is only integer 3 is presented even number of times — the answer is 3.
In the third query only integer 1 is written down — the answer is 1.
In the fourth query all array elements are considered. Only 1 and 2 are presented there even number of times. The answer is 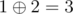 .
.
In the fifth query 1 and 3 are written down. The answer is 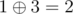 .
.
codeforces 703D Mishka and Interesting sum 偶数亦或 离线+前缀树状数组的更多相关文章
- Codeforces 703D Mishka and Interesting sum 离线+树状数组
链接 Codeforces 703D Mishka and Interesting sum 题意 求区间内数字出现次数为偶数的数的异或和 思路 区间内直接异或的话得到的是出现次数为奇数的异或和,要得到 ...
- Codeforces 703D Mishka and Interesting sum(离线 + 树状数组)
题目链接 Mishka and Interesting sum 题意 给定一个数列和$q$个询问,每次询问区间$[l, r]$中出现次数为偶数的所有数的异或和. 设区间$[l, r]$的异或和为$ ...
- Codeforces 703D Mishka and Interesting sum(树状数组+扫描线)
[题目链接] http://codeforces.com/contest/703/problem/D [题目大意] 给出一个数列以及m个询问,每个询问要求求出[L,R]区间内出现次数为偶数的数的异或和 ...
- CodeForces 703D Mishka and Interesting sum
异或运算性质,离线操作,区间求异或和. 直接求区间出现偶数次数的异或和并不好算,需要计算反面. 首先,很容易求解区间异或和,记为$P$. 例如下面这个序列,$P = A[1]xorA[2]xorA[3 ...
- CF #365 703D. Mishka and Interesting sum
题目描述 D. Mishka and Interesting sum的意思就是给出一个数组,以及若干询问,每次询问某个区间[L, R]之间所有出现过偶数次的数字的异或和. 这个东西乍看很像是经典问题, ...
- Codeforces Round #510 (Div. 2) D. Petya and Array(离散化+反向树状数组)
http://codeforces.com/contest/1042/problem/D 题意 给一个数组n个元素,求有多少个连续的子序列的和<t (1<=n<=200000,abs ...
- Codeforces Round #198 (Div. 1) D. Iahub and Xors 二维树状数组*
D. Iahub and Xors Iahub does not like background stories, so he'll tell you exactly what this prob ...
- Playrix Codescapes Cup (Codeforces Round #413, rated, Div. 1 + Div. 2) C. Fountains 【树状数组维护区间最大值】
题目传送门:http://codeforces.com/contest/799/problem/C C. Fountains time limit per test 2 seconds memory ...
- Codeforces Round #590 (Div. 3)【D题:26棵树状数组维护字符出现次数】
A题 题意:给你 n 个数 , 你需要改变这些数使得这 n 个数的值相等 , 并且要求改变后所有数的和需大于等于原来的所有数字的和 , 然后输出满足题意且改变后最小的数值. AC代码: #includ ...
随机推荐
- javascript实现新浪微博MID与地址转换
新浪微博每一条微博都会有一个mid,然后每条微博都有一个独立的地址,例如:http://www.weibo.com//Bw3SXzWzP 规律:地址中的黄色部分是用户id,绿色部分是微博的识别字符串, ...
- SpringBoot15 sell01 项目创建、MySQL数据库连接、日志配置、开发热部署、商品信息模块
项目软件版本说明: jdk: 1.8 springboot: 2.0.1 mysql: 5.7 1 项目创建 创建一个SpringBoot项目即可,创建是勾选 web jpa mysql 这三个依赖就 ...
- Luogu 3261 [JLOI2015]城池攻占
BZOJ 4003 需要实现一个可并堆. 每个点维护一个小根堆,然后一开始把所有骑士加入到它所在的点的小根堆当中,实际上空间是$O(m)$的,然后我们从上到下不断合并这个小根堆,合并完之后如果遇到堆顶 ...
- 修改laravel中的pagination的样式
运行如下命令,拷贝出pagination样式到public/vendor目录下, 然后在pagination实例上调用links(‘传路径’)方法 使用起来非常方便,同时也可以自定义样式
- 半平面交 (poj 1279(第一道半平面NlogN)完整注释 )
半平面交的O(nlogn)算法(转载) 求n个半平面的交有三种做法: 第一种就是用每个平面去切割已有的凸多边形,复杂度O(n^2). 第二种就是传说中的分治算法.将n个半平面分成两个部分,分别求完交之 ...
- 通过批处理操作注册表实现winform应用中Webbrowser以指定的IE版本加载网页
通过批处理操作注册表实现winform应用中Webbrowser以指定的IE版本加载网页 rem 强制WebBrowser控件使用指定IE版本显示应用的网页 IF EXIST %windir%\Sys ...
- .Net插入大批量数据
1. 使用SqlDataAdapter /// <summary> /// 实现数据库事务,大批量新增数据 /// </summary> ...
- 制作3D旋转视频展示区
CSS3 3D变形制作视频展示区 <!doctype html> <html lang="en"> <head> <meta charse ...
- Mapper配置文件夹
<?xml version="1.0" encoding="UTF-8" ?><!DOCTYPE mapperPUBLIC "-// ...
- HTML总结之:HTML5的DOCTYPE 与 meta 属性介绍
HTML5头部常用介绍: [DOCTYPE html] 声明文档类型为HTML5文件. [meta标签] <meta> 元素可提供有关页面的元信息(meta-information), ...
