决策树ID3算法--python实现

参考：

统计学习方法》第五章决策树】   http://pan.baidu.com/s/1hrTscza

决策树的python实现     有完整程序    

决策树（ID3、C4.5、CART、随机森林）    对决策树的python实现进行了详细的介绍

用Python开始机器学习（2：决策树分类算法）     特别

决策树（三）--完整总结（ID3，C4.5，CART,剪枝，替代）   理论

 

 #coding:utf-8
 # ID3算法，建立决策树
 import numpy as np
 import math
 import uniout
 '''
 #创建数据集
 def creatDataSet():
     dataSet = np.array([[1,1,'yes'],
                         [1,1,'yes'],
                         [1,0,'no'],
                         [0,1,'no'],
                         [0,1,'no']])
     features = ['no surfaceing', 'fippers']
     return dataSet, features
 '''

 #创建数据集
 def createDataSet():
     dataSet = np.array([['青年', '否', '否', '否'],
                   ['青年', '否', '否', '否'],
                   ['青年', '是', '否', '是'],
                   ['青年', '是', '是', '是'],
                   ['青年', '否', '否', '否'],
                   ['中年', '否', '否', '否'],
                   ['中年', '否', '否', '否'],
                   ['中年', '是', '是', '是'],
                   ['中年', '否', '是', '是'],
                   ['中年', '否', '是', '是'],
                   ['老年', '否', '是', '是'],
                   ['老年', '否', '是', '是'],
                   ['老年', '是', '否', '是'],
                   ['老年', '是', '否', '是'],
                   ['老年', '否', '否', '否']])
     features = ['年龄', '有工作', '有自己房子']
     return dataSet, features

 #计算数据集的熵
 def calcEntropy(dataSet):
     #先算概率
     labels = list(dataSet[:,-1])
     prob = {}
     entropy = 0.0
     for label in labels:
         prob[label] = (labels.count(label) / float(len(labels)))
     for v in prob.values():
         entropy = entropy + (-v * math.log(v,2))
     return entropy

 #划分数据集
 def splitDataSet(dataSet, i, fc):
     subDataSet = []
     for j in range(len(dataSet)):
         if dataSet[j, i] == str(fc):
             sbs = []
             sbs.append(dataSet[j, :])
             subDataSet.extend(sbs)
     subDataSet = np.array(subDataSet)
     return np.delete(subDataSet,[i],1)

 #计算信息增益，选择最好的特征划分数据集，即返回最佳特征下标
 def chooseBestFeatureToSplit(dataSet):
     labels = list(dataSet[:, -1])
     bestInfoGain = 0.0   #最大的信息增益值
     bestFeature = -1   #*******
     #摘出特征列和label列
     for i in range(dataSet.shape[1]-1):     #列
         #计算列中，各个分类的概率
         prob = {}
         featureCoulmnL = list(dataSet[:,i])
         for fcl in featureCoulmnL:
             prob[fcl] = featureCoulmnL.count(fcl) / float(len(featureCoulmnL))
         #计算列中，各个分类的熵
         new_entrony = {}    #各个分类的熵
         condi_entropy = 0.0   #特征列的条件熵
         featureCoulmn = set(dataSet[:,i])   #特征列
         for fc in featureCoulmn:
             subDataSet = splitDataSet(dataSet, i, fc)
             prob_fc = len(subDataSet) / float(len(dataSet))
             new_entrony[fc] = calcEntropy(subDataSet)   #各个分类的熵
             condi_entropy = condi_entropy + prob[fc] * new_entrony[fc]    #特征列的条件熵
         infoGain = calcEntropy(dataSet) - condi_entropy     #计算信息增益
         if infoGain > bestInfoGain:
             bestInfoGain = infoGain
             bestFeature = i
     return bestFeature

 #若特征集features为空，则T为单节点，并将数据集D中实例树最大的类label作为该节点的类标记，返回T
 def majorityLabelCount(labels):
     labelCount = {}
     for label in labels:
         if label not in labelCount.keys():
             labelCount[label] = 0
         labelCount[label] += 1
     return max(labelCount)

 #建立决策树T
 def createDecisionTree(dataSet, features):
     labels = list(dataSet[:,-1])
     #如果数据集中的所有实例都属于同一类label，则T为单节点树，并将类label作为该结点的类标记，返回T
     if len(set(labels)) == 1:
         return labels[0]
     #若特征集features为空，则T为单节点，并将数据集D中实例树最大的类label作为该节点的类标记，返回T
     if len(dataSet[0]) == 1:
         return majorityLabelCount(labels)
     #否则，按ID3算法就计算特征集中各特征对数据集D的信息增益，选择信息增益最大的特征beatFeature
     bestFeatureI = chooseBestFeatureToSplit(dataSet)  #最佳特征的下标
     bestFeature = features[bestFeatureI]    #最佳特征
     decisionTree = {bestFeature:{}} #构建树，以信息增益最大的特征beatFeature为子节点
     del(features[bestFeatureI])    #该特征已最为子节点使用，则删除，以便接下来继续构建子树
     bestFeatureColumn = set(dataSet[:,bestFeatureI])
     for bfc in bestFeatureColumn:
         subFeatures = features[:]
         decisionTree[bestFeature][bfc] = createDecisionTree(splitDataSet(dataSet, bestFeatureI, bfc), subFeatures)
     return decisionTree

 #对测试数据进行分类
 def classify(testData, features, decisionTree):
     for key in decisionTree:
         index = features.index(key)
         testData_value = testData[index]
         subTree = decisionTree[key][testData_value]
         if type(subTree) == dict:
             result = classify(testData,features,subTree)
             return result
         else:
             return subTree

 if __name__ == '__main__':
     dataSet, features = createDataSet()     #创建数据集
     decisionTree = createDecisionTree(dataSet, features)   #建立决策树
     print 'decisonTree：',decisionTree

     dataSet, features = createDataSet()
     testData = ['老年', '是', '否']
     result = classify(testData, features, decisionTree)  #对测试数据进行分类
     print '是否给',testData,'贷款：',result

相关理论：

决策树

概念原理

决策树是一种非参数的监督学习方法，它主要用于分类和回归。决策树的目的是构造一种模型，使之能够从样本数据的特征属性中，通过学习简单的决策规则——IF THEN规则，从而预测目标变量的值。

决策树学习步骤：1 特征选择 2 决策树的生成 3 决策树的修剪

那么如何进行特征选择：

由于特征选择的方法不同，衍生出了三种决策树算法：ID3、C4.5、CART

ID3信息增益

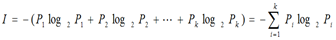熵越大，随机变量的不确定性越大。

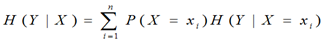条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性。

在信息增益中，衡量标准是看特征能够为分类系统带来多少信息，带来的信息越多，该特征越重要。对一个特征而言，系统有它和没它时信息量将发生变化，而前后信息量的差值就是这个特征给系统带来的信息量。所谓信息量，就是熵。

C4.5信息增益比

CART 基尼指数

基尼指数越大，样本的不确定性就越大

三个算法的优缺点

ID3算法	C4.5算法	CART算法（Classification and Regression Tree）
以信息增益为准则选择信息增益最大的属性。 缺点：1）信息增益对可取值数目较多的属性有所偏好，比如通过ID号可将每个样本分成一类，但是没有意义。 2）ID3只能对离散属性的数据集构造决策树。 鉴于以上缺点，后来出现了C4.5算法。	以信息增益率为准则选择属性；在信息增益的基础上对属性有一个惩罚，抑制可取值较多的属性，增强泛化性能。 其他优点： 1）在树的构造过程中可以进行剪枝，缓解过拟合； 2）能够对连续属性进行离散化处理（二分法）； 3）能够对缺失值进行处理； 缺点：构造树的过程需要对数据集进行多次顺序扫描和排序，导致算法低效； 刚才我们提到 信息增益对可取值数目较多的属性有所偏好；而信息增益率对可取值数目较少的属性有所偏好！OK，两者结合一下就好了！ 解决方法：先从候选属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。而不是大家常说的 直接选择信息增益率最高的属性！	顾名思义，可以进行分类和回归，可以处理离散属性，也可以处理连续的。 分类树使用GINI指数来选择划分属性：在所有候选属性中，选择划分后GINI指数最小的属性作为优先划分属性。回归树就用最小平方差。

ID3、C4.5、CART区别   参考：https://www.zhihu.com/question/27205203?sort=created