poj2778 AC自动机

以下内容均为转载，，只有代码是自己写的=-=

http://blog.csdn.net/morgan_xww/article/details/7834801   转载地址 博主写的很好

---------------------------------------------------------------------------------------我是分割线

DNA Sequence

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 16585		Accepted: 6408

Description

It's well known that DNA Sequence is a sequence only contains A, C, T and G, and it's very useful to analyze a segment of DNA Sequence，For example, if a animal's DNA sequence contains segment ATC then it may mean that the animal may have a genetic disease. Until now scientists have found several those segments, the problem is how many kinds of DNA sequences of a species don't contain those segments.

Suppose that DNA sequences of a species is a sequence that consist of A, C, T and G，and the length of sequences is a given integer n.

Input

First line contains two integer m (0 <= m <= 10), n (1 <= n <=2000000000). Here, m is the number of genetic disease segment, and n is the length of sequences.

Next m lines each line contain a DNA genetic disease segment, and length of these segments is not larger than 10.

Output

An integer, the number of DNA sequences, mod 100000.

Sample Input

4 3
AT
AC
AG
AA

Sample Output

36

•题意：有m种DNA序列是有疾病的，问有多少种长度为n的DNA序列不包含任何一种有疾病的DNA序列。（仅含A,T,C,G四个字符）

•样例m=4,n=3,{“AA”,”AT”,”AC”,”AG”}

•答案为36，表示有36种长度为3的序列可以不包含疾病

 

这个和矩阵有什么关系呢？？？

•上图是例子{“ACG”,”C”},构建trie图后如图所示，从每个结点出发都有4条边（A,T,C,G）

•从状态0出发走一步有4种走法：

  –走A到状态1（安全）；

  –走C到状态4（危险）；

  –走T到状态0（安全）；

  –走G到状态0（安全）；

•所以当n=1时，答案就是3

•当n=2时，就是从状态0出发走2步，就形成一个长度为2的字符串，只要路径上没有经过危险结点，有几种走法，那么答案就是几种。依此类推走n步就形成长度为n的字符串。

•建立trie图的邻接矩阵M：

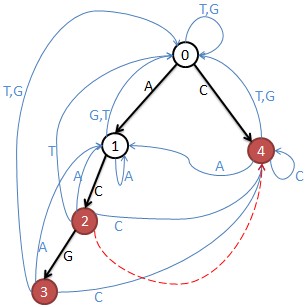
2 1 0 0 1

2 1 1 0 0

1 1 0 1 1

2 1 0 0 1

2 1 0 0 1

M[i,j]表示从结点i到j只走一步有几种走法。

那么M的n次幂就表示从结点i到j走n步有几种走法。

注意：危险结点要去掉，也就是去掉危险结点的行和列。结点3和4是单词结尾所以危险，结点2的fail指针指向4，当匹配”AC”时也就匹配了”C”，所以2也是危险的。

矩阵变成M：

2 1

2 1

计算M[][]的n次幂，然后 Σ(M[0,i]) mod 100000 就是答案。

由于n很大，可以使用二分来计算矩阵的幂

#include<cstdio>
#include<map>
#include<queue>
#include<cstring>
#include<algorithm>
typedef long long ll;
using namespace std;
const int N=101;
const int mod=1e5;
struct Mat
{
    ll mat[N][N];
    Mat operator *(const Mat &B)const
    {
        Mat C;
        memset(C.mat,0,sizeof(C.mat));
        for(int k=0; k<N; ++k)
        {
            for(int i=0; i<N; ++i)
            {
                if(mat[i][k]==0) continue;
                for(int j=0; j<N; ++j)
                {
                    if(B.mat[k][j]==0) continue;
                    C.mat[i][j]=(C.mat[i][j]+mat[i][k]*B.mat[k][j])%mod;
                }
            }
        }
        return C;
    }
    int operator ^(int &k)
    {
        Mat C;
        memset(C.mat,0,sizeof(C.mat));
        for(int i=0; i<N; ++i)
            C.mat[i][i]=1;
        while(k)
        {
            if(k&1)
            {
                C=C*(*this);
                --k;
            }
            k>>=1;
            (*this)=(*this)*(*this);
        }
        int cnt=0;
        for(int i=0; i<N; ++i)
            cnt=(cnt+C.mat[0][i])%mod;
        return cnt;
    }
};
struct AC{
     int ch[58][4],fail[58],val[58],sz,rt,id[128];
     void init(){
        sz=rt=0;
        memset(ch[rt],-1,sizeof(ch[rt]));
        id['A']=0,id['G']=1,id['T']=2,id['C']=3;
     }
     void insert(char *str){
        int u=rt,len=strlen(str);
        for(int i=0;i<len;++i){
            int op=id[str[i]];
            if(ch[u][op]==-1) {
                ++sz;
                memset(ch[sz],-1,sizeof(ch[sz]));
                val[sz]=0;
                ch[u][op]=sz;
            }
            u=ch[u][op];
        }
        val[u]=1;
     }
     void build(){
        queue<int>Q;
        int u=rt;
        for(int i=0;i<4;++i){
            if(ch[u][i]==-1) ch[u][i]=rt;
            else {
                fail[ch[u][i]]=rt;
                Q.push(ch[u][i]);
            }
        }
        while(!Q.empty()){
            u=Q.front();
            Q.pop();
            val[u]|=val[fail[u]];
            for(int i=0;i<4;++i){
                if(ch[u][i]==-1) ch[u][i]=ch[fail[u]][i];
                else {
                    fail[ch[u][i]]=ch[fail[u]][i];
                    Q.push(ch[u][i]);
                }
            }
        }
     }
     void work(int n){
        Mat A;
        memset(A.mat,0,sizeof(A.mat));
        for(int i=0;i<=sz;++i)
            for(int j=0;j<4;++j)
            if(!val[ch[i][j]]) ++A.mat[i][ch[i][j]];
        printf("%d\n",A^n);
     }
}ac;
char s[55];
int main(){
    int m,n;
    while(scanf("%d%d",&m,&n)!=EOF){
        ac.init();
        while(m--){
            scanf("%s",s);
            ac.insert(s);
        }
        ac.build();
        ac.work(n);
    }
}