ggplot2（1） 简介

1.1 简介

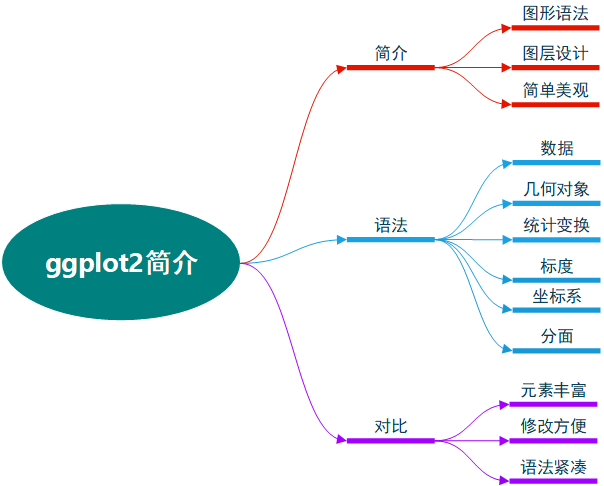
ggplot2是一个用来绘制统计图形（数据图形）的R软件包，与其他大多数的图形软件包不同，ggplot2是由其背后的一套图形语法所支持的。ggplot2可以绘制出很多美观度的图形，同时能避免诸多繁琐的细节。用ggplot2绘图时，图形的每个部分可以一次进行构建，之后还可以进行编辑。ggplot2采用了图层的设计方式。

1.2 图形的语法

一张统计图形就是从数据到几何对象（点、线、条形等）的图形属性（颜色、形状、大小等）的一个映射。此外，图形中还可能包含数据的统计变换，最后绘制在某个特定的坐标系。

• 数据：最基础的部分是将数据中的变量对应到图形属性的映射；
• 几何对象：代表在图中实际展现的点、线、多边形等元素；
• 统计变换：是对数据进行的某种汇总，例如，将数据分组计数及创建直方图，或将一个二维的关系同线性模型进行解释，统计变换是可选的，到通常非常有用；
• 标度：将数据的取值映射到图形空间，例如，用颜色、大小或形状来表示不同的取值，展现标度的常见做法是绘制图例和坐标轴；
• 坐标系：描述了数据是如何映射到图形所在的平面的，它同时提供了看图所需的坐标系和网格线；
• 分面：描述了如何将数据分解为各个子集，以及如何对子集作图并联合进行展示。

1.3 ggplot2和其他R软件包的对比

• 基础图形系统基于实现S语言图形驱动的经验，采用“纸-笔”模式，只能在图形的最顶端进行绘图，而不能修改或删除已有的内容，除了已经呈现在屏幕上的图像之外，图形没有其他的表达形式，，如层次、结构、元素类型等；
• 网格图形系统是一个更加丰富的绘制基本图形元素的系统，其中的图形对象可以与屏幕上的图像独立存在，并且可以反复修改，其中一系列的视图区可以方便地对图形进行复杂的布局；
• lattice是对基础绘图系统的巨大改进，在此可以方便地进行条件作图，并且其中的一些作图细节或自动地完成；
• ggplot2能够创建任何类型的统计图形，其背后的模型使得用户可以用紧凑的语法轻松地绘制出许多图形，而且其中独立的图形部件使得图形的可扩展性很强。

总结