q检验|新复极差法|LSD|二因素方差分析

生物统计与实验设计

放大程度q检验：精度较高>新复极差法：各种错误比较平均>LSD

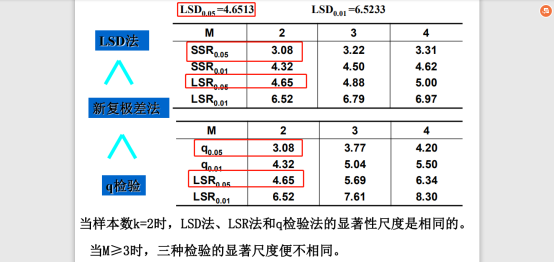
其中，LSD不随M的变化而变化，但是SSR和q-test会随M变化而变化。

第一步代表了方差分析的核心思想

第二步F检验与t检验同理

第三步只知道一组因素是否有差异，而不知道何种水平有差异，需要多重比较。

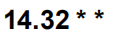打星号表示极显著

二因素方差分析：

主效应是各试验因素独立作用。

互作是各试验因素不独立作用，即因素A与因素B组成一个超级因素。

要保证所有样本条件一致，即SE相同，虽然此要求在实际情况中无法达到，但是单从主要矛盾角度考虑，则可忽略。

单看一个因素时，其他因素差异忽略。

环境需要提取主要矛盾，关系是环境因素与滞育期长短的函数关系（回归分析），或者不同环境因素造成的滞育期长短是否有差异（方差分析）。

在得到互作差异不显著之后，可以尝试使用非重复的二因素分析，看SE是否是正态分布。这之后，根据非重复的二因素分析结果，如果有因素不显著之后，可以把该因素归为次要因素，因此建立单因素方差分析。对于第一次退回分析是必要的，但是第二次是不必要的，因为非重复的单因素方差分析与二因素方差分析原理是一致的，都是针对treatment，而重复方差分析中针对随机因素。