最长回文子窜O(N)

字符窜同构的性质：同构字符窜拥有最小和最大的表示方法；

最长回文子窜：

1.首先暴力法：（n三方）

枚举每个起点和终点，然后单向扫描判断是不是回文子窜；

2.中心扩散法，（N方）

枚举每个中点，向外扩散，看以他为中心的回文子窜的长度是多少；

易证：复杂度N方

3.O(N)的做法；

https://blog.csdn.net/afei__/article/details/83214042?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task；

我的理解：和扩展KMP有点相似，扩展KMP,我们为了不重复所以设定了破，po和ex[po]，然后我们讨论i可能的答案是否已经包含在扫描的里面了，如果包含了直接赋值，没包含继续扫描；

我们对中心扩散的方法进行改进，

1.思想：    1）将原字符串S的每个字符间都插入一个永远不会在S中出现的字符（本例中用“#”表示），在S的首尾也插入该字符，使得到的新字符串S_new长度为2*S.length()+1，保证Len的长度为奇数(下例中空格不表示字符，仅美观作用)；

例：S：       a  a  b  a  b  b  a

S_new:        #  a  #  a  #  b  #  a  #  b  #  b  #  a  #

2）根据S_new求出以每个字符为中心的最长回文子串的最右端字符距离该字符的距离，存入Len数组中，即S_new[i]—S_new[r]为S_new[i]的最长回文子串的右段（S_new[2i-r]—S_new[r]为以S_new[i]为中心的最长回文子串），Len[i] = r - i + 1;

S_new:        #  a  #  a  #  b  #  a  #  b  #  b  #  a  #

Len:            1  2  3  2  1   4  1  4  1  2  5   2  1  2  1

Len数组性质：Len[i] - 1即为以Len[i]为中心的最长回文子串在S中的长度。在S_new中，以S_new[i]为中心的最长回文子串长度为2Len[i] - 1，由于在S_new中是在每个字符两侧都有新字符“#”，观察可知“#”的数量一定是比原字符多1的，即有Len[i]个，因此真实的回文子串长度为Len[i] - 1，最长回文子串长度为Math.max(Len) - 1。

3）Len数组求解（线性复杂度（O(n)））：

a.遍历S_new数组，i为当前遍历到的位置，即求解以S_new[i]为中心的最长回文子串的Len[i];

b.设置两个参数：sub_midd = Len.indexOf(Math.max(Len)表示在i之前所得到的Len数组中的最大值所在位置、sub_side = sub_midd + Len[sub_midd] - 1表示以sub_midd为中心的最长回文子串的最右端在S_new中的位置。起始sub_midd和sub_side设为0，从S_new中的第一个字母开始计算，每次计算后都需要更新sub_midd和sub_side；

c.当i < sub_side时，取i关于sub_midd的对称点j（j = 2sub_midd - i，由于i <= sub_side，因此2sub_midd - sub_side <= j <= sub_midd);当Len[j] < sub_side - i时，即以S_new[j]为中心的最长回文子串是在以S_new[sub_midd]为中心的最长回文子串的内部，再由于i、j关于sub_midd对称，可知Len[i] = Len[j];    当Len[j] >= sub.side - i时说明以S_new[i]为中心的回文串可能延伸到sub_side之外，而大于sub_side的部分还没有进行匹配，所以要从sub_side+1位置开始进行匹配，直到匹配失败以后，从而更新sub_side和对应的sub_midd以及Len[i]；

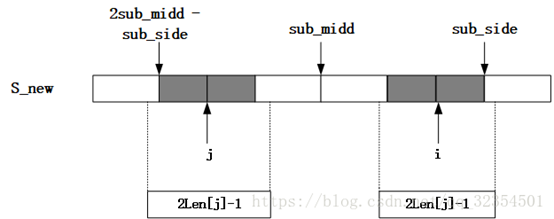
d.当i > sub_side时，则说明以S_new[i]为中心的最长回文子串还没开始匹配寻找，因此需要一个一个进行匹配寻找，结束后更新sub_side和对应的sub_midd以及Len[i]。

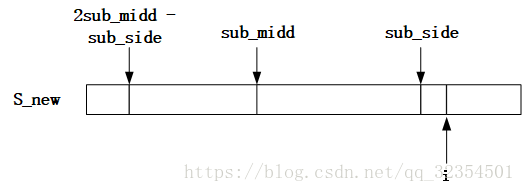
我的理解：

实际上我们每次扫描得到了sub_mid和sub_side,利用回文串的对称性，我们来判断是否已经在答案里面了，不在的我们就继续扫描比较下去；

就是对中心扩散法的一种dp；

与那个啥z函数有点类似的想法，利用性质推到到已经求过的内容然后及进行求解，避免重复扫描；

void getlen(char *str)
{
 int ans=1,arm=0;
 memset(len,0,sizeof(len));
 int mid=0,side=1,i,j,r;
 len[0]=1;
 for(i=1;i<R;i++)
 {
  j=2*mid-i;
  if(j<0||j-len[j]<=mid-len[mid])
  {
   r=side-i;
   if(r==0) side++,r=1;
   while(i-r>=0&&str[i-r]==str[side])
   {
    r++;
    side++;
   }
   mid=i;
   len[i]=r;
  }
  else
   len[i]=len[j];
  if(ans<len[i])
  {
   ans=len[i];
   arm=i;
  }
 }
 if(ans-1<2)
 cout<<"No solution!\n";
 else
 {
  int r=arm+len[arm]-1,l=arm-(len[arm]-1);
  r--;
  l=l/2;r=r/2;
  cout<<l<<" "<<r<<"\n";
  for(int i=l;i<=r;i++)
   slove(s1[i]);
  cout<<"\n";
 }
}