网络流二十四题，题解summary

没有全部写完，有几题以后再补吧。

第一题：最简单的：飞行员配对方案问题

讲讲这个题目为什么可以用网络流？

因为这个题目是要进行两两之间的匹配，这个就可以想到用二分图匹配，二分图匹配又可以用网络流写。

为什么二分图匹配可以用网络流写呢？

你在二分图上面加一个源点和一个汇点，然后你求从源点到汇点的最大流，这个是不是就是二分图的最大匹配。

第二题：最小路径覆盖问题

这个题目是一个特别明显的二分图问题，也用到了一个比较常见的方法拆点法，

这个再介绍一下拆点法这个网络流里面的基本套路该什么时候用，

如果你碰到一个网络流的题目，题目对每一个点有次数限制，这个时候就需要对这个点进行拆分。

拆分的方法有很多种，这个可以慢慢积累，也没有特别重要。

这个题目如果你对二分图定理很了解，这个就会是一个比较简单的题目了，可以学习一下二分图的定理

主要有三个：最小顶点覆盖数=最大匹配数   最大独立集=总数-最小定点覆盖数   有向无环图（DAG）最小路径覆盖数=原图上的点数-最大匹配数

这几个概念再很多地方都可以看到，尤其是最大独立集。

这个题目就是直接让你求一个图的最小路径覆盖数，这个对每一个点也有次数限制，每个点只能用一次，所以这个就要用拆分法，

不过这个题目所用的拆分法有一点点不同，一般题目都是把一个点拆成两个点，然后把这两个点连起来，连起来的这条直线的容量为1.

但是碰到这个二分图匹配问题，如果你这么连，很显然是没有意义的。

然后再分析：这个最小路径覆盖，最多的肯定是n，一共有n个点，然后我们在合并的过程中路径数量不断减少。

所以这个题目最小路径覆盖数，就是本来有的n个点再减去可以两两合并的数。

最后就是输出，这个输出就自己看代码吧。

第三题：魔术球问题

这个题目也是一个二分图问题，我觉得不是那么简单吧。

给你的柱子数就是最小路径数，放球条件就是建图条件，让你求可以放的最多的球数量，就是最多的点满足可以满足这个图。

这个题目要拆分，一个点连接源点，一个连接汇点，这被拆的两个点不能连起来。

每一个球，就先去遍历，如果可以和之前的一些球有建图条件，就先建图，建完图之后跑最大流（增光路），如果增广路不为0，

那就说明这个可以放在之前用的柱子里面，不然就再开一个柱子，如果柱子数最后达到n，就跳出循环。

这个为什么说增广路不为0，就说明可以放在之前的柱子里面呢？这个是因为，我们对于每一条线得容量都设为1，

所以这个就说明，每新增加一个球，如果增广路不是0，则说明它肯定和之前柱子的最上面的那个球连在了一起。

因为和下面的球就算连在了一起，也没办法增广了（容量为1）

知道了，这些建图就很简单了。这个是一个很巧妙的建图。

可以看下面的图片理解一下。

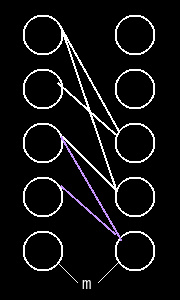
第四题：圆桌问题

这个是一个二分图的多重匹配，这个题目比较简单，这个多种匹配就直接跑一个最大流好了。

题目不是要求同一个单位的人不能坐在一起吗？那就每一个单位都向每一个桌子连一条容量为1的线，这个就可以保证

不会有一个单位的人坐在一起了，如果最大流大于等于所有单位人之和，那就可以满足，否则就不可以。

为什么会这么想呢？这个是因为我首先知道这个是一个网络流的题目，我需要建图，然后就很好做了。

第五题：试题库问题

这个题目就不说了，这个题目和圆桌问题简直一模一样。

第六题：最长不下降子序列

这个题目建图很难想，第一问就是一个裸的LIS，

主要就是第二问，这个题目我是没有想到，看了一下题解，首先要进行拆点，因为每一个点只能用一次。

这个建图就是先对这个序列进行处理，怎么处理呢？求出f数组，f[i]代表到第i位的最长不下降子序列，

如果f[i]==1，那就直接和源点相连，然后之后如果满足a[i]>=a[j]&&i>j&&f[i]==f[j]+1

那么就把j的出点和i的入点连起来。

这个就是建图，这个样子建图好难想啊。

不过看了题解之后也没有觉得特别难了，这个更加具体的解析就看看博客吧。

第七题：餐巾计划问题

这个题目的建图很难想，一般就看看题目然后就看题解了。

这个是把每一天拆成了两个点，一个上午点和一个下午点。
下午点都和源点相连表示一天的结束，上午点和汇点相连，表示需要的餐巾数量。
与源点和汇点相连的点的cap都设置成这一天需要的餐巾数量，这个来限制送去快洗和慢洗的毛巾数。
然后再去处理3+1，3表示快洗，慢洗，新买，1表示不洗。因为之前以及被限制过了，
所以这里的不需要再去考虑有多少脏毛巾，这里的cap应该设置成inf，因为一次可以洗无数条毛巾。
这个不洗的要好好处理，这个不洗表示直接积累到下一天，那么就说明，这个的cost=0，
但是我们会疑惑，如果这样会不会影响到网络流？ 其实这个不会，因为餐巾的积累会往下一天的晚上传递，意思
是说，这个餐巾不会算作这一天需要的餐巾数，但是那为什么还要连边呢？这个连边会让它往下一天传递，
那么餐巾积累，之后可以考虑一起洗掉。一起洗一堆和一次洗一条所用的时间是一样的，
所以如果我们之后再堆在一起洗也许会更优。

这个题目，第一个是要用到拆点把一天拆成上午和下午，第二个是转移，不洗就之间向下一天转移费用为0，买新的就从源点向这一天的上午

直接相连费用为新毛巾的费用，快洗就把这一天向洗好的早上相连，费用为快洗的费用，慢洗同理。

第八题：P2770 航空路线问题

这个也是一个费用流的问题，这个知识把求最小费用改成求最大费用，这个改法有两种，一种就是把d改成-inf or 0xef

然后就是一个模板题了。

输出需要注意

第九题：数字梯形问题

第一问：这一问要进行拆点和边权限制，用拆点来保证每一个数字只被经过一次

第二问：这一问就不需要拆点了，只需要边权限制

第三位：这一问没有任何限制，就是源点和第一行的数字相连容量为1 .

第十题：运输问题

这个也是一个裸的最大费用最大流和最小费用最大流的问题

第十一题：P4014 分配问题

同上

第十二题：负载平衡

这个题目应该也是把仓库进行拆点，因为这个仓库是环状摆放，并且只能向两边进行转移，

所以就把每一个仓库进行拆点，入点和源点相连，容量为这个仓库货物数量，费用为0，然后每一个仓库入点和左右的仓库的出点相连。

费用为1，然后每一个仓库的出点和汇点相连，所以最后的最小费用就是搬运量。

第十三题：深海机器人

这个题目通过数据范围判断出这个是一个网络流，

建图就是每一个位置的机器人可以走到的下一个位置。因为这个直接给的就是路径的权值不是点的权值，所以就不需要进行拆分。

第十四题：火星探险问题

这个题目和上面是一样的，只不过给的是点的权值，所以需要进行拆分。

第十五题：最长k可重区间集问题

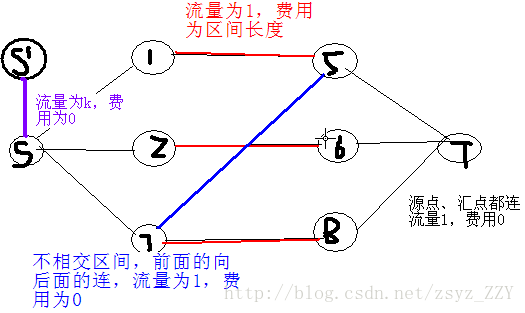
这个题目的建图很巧妙,我也讲不清楚。

第十六题：最长k可重线段集问题

这个题目和上面那个是一样的，只不过可能有就是平行于y轴的直线，这个需要处理一下，这个也是要连的。