JZOJ-2019-11-5 A组

T1

给定由 n 个点 m 条边组成的无向连通图，保证没有重边和自环。

你需要找出所有边，满足这些边恰好存在于一个简单环中。一个环被称为简单环，当且仅当它包含的所有点都只在这个环中被经过了一次。(即求\(\oplus \{id((u,v)) | (u,v) \in E 且 (u,v)在且仅在一个环上\}\))

注意到这些边可能有很多条，你只需要输出他们编号的异或和即可。

Input

第一行两个数 n, m。

接下来 m 行，每行两个数 ai , bi，表示第 i 条边连接了 ai , bi。

Output

输出一个数，表示所有满足条件的边的编号的异或和。

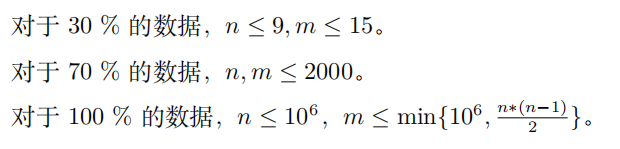
前置知识

解法1

树上差分, LCA, 巨大码力

解法2

Tarjan 算法求强连通分量

解法1

可以先 dfs 出一棵生成树。

因为是无向图，生成树上的非树边都是返祖边，我们容易发现，若一条边恰好在一个简单环内，那么它满足下面下面两个条件之一：

• 返祖边，且它覆盖的树边不和任何其他返祖边覆盖的树边有公共边。
• 树边且被一条返祖边覆盖，覆盖它的返祖边覆盖的树边不和其他返祖边覆盖的树边有公共
  
  边。

可以先对于每条树边 O(n) 求出被多少条返祖边覆盖，然后对于每条返祖边 O(m) 计算是否跟其他返祖边有重合。时间复杂度 O(nm)。计算被多少返祖边覆盖可以利用树上差分的思想做到 O(m)，计算是否有重合相当于链上查询，也可以利用差分做到 O(m)。时间复杂度 O(n + m)。代码贼难写考场上数组开多MLE了血亏100pts

解法2

考虑求出所有的点双连通分量。首先这个点双连通分量里的边要合法的话，那么内部的边数一定大等于点数（因为有环）。其次这个点双连通分量里如果边数大于点数，那么所有边可以由两个不同的环覆盖。

也就是说，我们只需要求出所有的点双连通分量，然后把那些点数等于边数的点双连通分量内部的边标记为合法即可。利用 \(Tarjan\) 算法求强连通分量可以做到 \(O(n + m)\)。

代码

/*code by tyqtyq*/
#include<vector>
#include<cstdio>
#include<iostream>
#define f(i,x,y) for(register int i=x, i##end=y; i<=i##end; ++i)
#define d(i,x,y) for(register int i=y, i##end=x; i>=i##end; --i)
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define _ 2000005
using namespace std;
int read(int& x){x=0; int f=1, ch=getchar(); while(!isdigit(ch)) f=ch=='-'?-1:f, ch=getchar(); while(isdigit(ch)) x=x*10+ch-'0', ch=getchar(); return x*=f;}
int read(){int x=0, f=1, ch=getchar(); while(!isdigit(ch)) f=ch=='-'?-1:f, ch=getchar(); while(isdigit(ch)) x=x*10+ch-'0', ch=getchar(); return x*f;}
int max(int x, int y){return x>y?x:y;} int min(int x, int y){return x<y?x:y;}
int Next[_], ver[_], head[_], tot=1, dfn[_], low[_], cnt, stack[_], top, vis[_], V[_], ans;
vector<int> dcc, orz;
void add(int u, int v){ver[++tot]=v, Next[tot]=head[u], head[u]=tot;}
void dfs(int x){
	for(int i=head[x];i;i=Next[i]){
		if(!V[ver[i]]||vis[i]) continue;
		vis[i]=vis[i^1]=1;
		orz.push_back(i);
		dfs(ver[i]);
	}
}
void tarjan(int x, int root){
	dfn[x] = low[x] = ++cnt;
	stack[++top] = x;
	int flag=0;
	for(int i=head[x];i;i=Next[i]){
		int v=ver[i];
		if(!dfn[v]){
			tarjan(v, root); low[x]=min(low[x], low[v]);
			if(low[v] >= dfn[x]){
				++flag; int d; do{d=stack[top--]; dcc.push_back(d); V[d]=1;}while(d!=v); dcc.push_back(x); dfs(x) ;
				if(orz.size() == dcc.size()) for(auto j:orz) ans^=(j/2),vis[j]=vis[j^1]=0;
				for(auto j:dcc) V[j]=0; dcc.clear(); orz.clear();
			}
		}
		else low[x]=min(low[x], dfn[v]);
	}
}
int n, m;
int main(){
	read(n); read(m);
	f(i,1,m) {int x,y; read(x); read(y); add(x,y); add(y,x);}
	tarjan(1, 1);
	cout<<ans<<endl;
	return 0; //拜拜程序~
}

T2

\(Wayne\)喜欢看书，更喜欢买书。

某天\(Wayne\)在当当网上买书，买了很多很多书。\(Wayne\)有一个奇怪的癖好，就是第一本书的价格必须恰为\(X\)，而之后买的每一本书，若是比上一本更昂贵，则价格最多多\(A\)元；若是比上一本更便宜，则价格最多少\(B\)元。

\(Wayne\)心血来潮，一口气买了\(N\)本书，但他记不得每本书的价格了，只记得总价格是\(M\)。\(Wayne\)于是很想知道一种可能的书价分布。为了简化问题，我们假定书价的定义域是整数，且每本书与上一本书的价格差，要么恰为\(+A\)，要么恰为\(-B\)。

只要给出任意一个合法的书价序列就算正确。

Input

第一行一个正整数N。

第二行四个整数依次是X,A,B,M。

Output

输出一行N个整数，用空格隔开。数据保证有解。

Data Constraint

对于\(100%\)的数据，满足\(1 \leq A, B \leq 10^6，|X| \leq 10^6，N \leq 10^5\)，\(M\)可用带符号\(64\)位整型存储。

前置知识

推式子能力

解法

设买书编号为\(0-n\), \(a_i\)表示当前升了几次价格

对于\(a_i\), 总有\(a_i = a_{i-1} + 1\) 或 \(a_i = a_{i-1}\)成立, 且必有\(a_0 = 0\)

有总买书价格为\(\sum_{i=0}^{n} x + a_i \times A - (k-a_i) \times B\) = \(n \times x - B \times \frac{n \times (n+1)}{2} \sum_{i=0}^{n} a_i \times(A+B)\), 整理得\(\sum_{i=0} a_i = \frac{m - n \times x + B \times \frac{n \times (n+1)}{2}}{A+B}\)

因总有\(a_i = a_{i-1} + 1\) 或 \(a_i = a_{i-1}\)成立, 考虑求出差分序列\(\delta(a)\), 总有\(\delta(a)_i = 0\) 或 \(\delta(a)_i = 1\)成立, 做一遍整数拆分即可

代码

/*code by tyqtyq*/
#include<bits/stdc++.h>
#define f(i,x,y) for(register int i=x, i##end=y; i<=i##end; ++i)
#define d(i,x,y) for(register int i=y, i##end=x; i>=i##end; --i)
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define int long long
using namespace std;
int read(int& x){x=0; int f=1, ch=getchar(); while(!isdigit(ch)) f=ch=='-'?-1:f, ch=getchar(); while(isdigit(ch)) x=x*10+ch-'0', ch=getchar(); return x*=f;}
int read(){int x=0, f=1, ch=getchar(); while(!isdigit(ch)) f=ch=='-'?-1:f, ch=getchar(); while(isdigit(ch)) x=x*10+ch-'0', ch=getchar(); return x*f;}
int max(int x, int y){return x>y?x:y;} int min(int x, int y){return x<y?x:y;}
int n, a, b, m, x, suma, delta[100005];
signed main(){read(n); read(x); read(a); read(b) ; read(m); suma = m - n*x + ((n*(n-1))/2)*b; if((suma)%(a+b)) return puts("-1"), 0; else suma/=(a+b); int xa = 2; while(suma){ while(suma < n-xa+1 && xa<=n) ++xa ; if(xa == n+1) return puts("-1"), 0; else delta[xa] = 1, suma -= n-xa+1, ++xa;}f(i,2,n) { if(delta[i]) delta[i] = delta[i-1] + a; else delta[i] = delta[i-1] - b;} f(i,1,n) printf("%lld ", delta[i]+x) ; puts(""); return 0; /*拜拜程序*/ }

T3

Input

Output

若无解，则输出”Impossible”。

否则第一行输出”Possible”，第二行输出 n 个正整数，依次输出序列 a 中每个数。

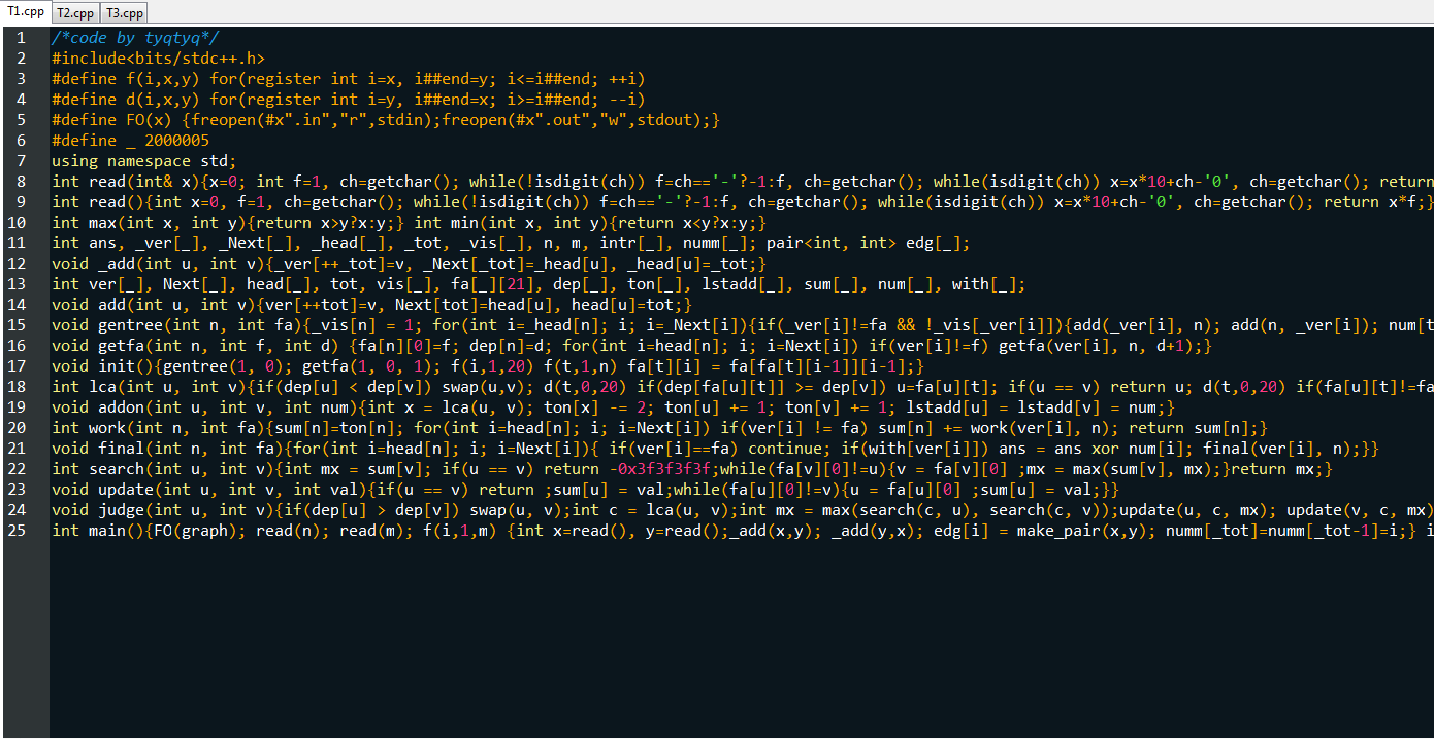
Data Constraint

解法

我们可以整理出一堆形如 \(xi − xj ≥ v\) 的式子。拓扑排序判环并求答案即可

注意到暴力连边级别是 \(O(n^2)\) 的。

不过我们可以建一些辅助点来优化一下状态，具体来说，先像线段树一样，每个点表示区间最大值，和子节点之间连长度为 \(0\) 的边。每次一个限制，先找到被 \(k\) 个点分割开的 \(k + 1\) 个区间，每个区间找到线树上对应的 \(O(log n)\) 个区间，然后新建一个点表示这些区间的最大值，与这些点连长度为 \(0\) 的边。最后 \(k\) 个点与这个点连长度为 \(1\) 的边。

这样的连边级别是 \(O(k log n)\) 的