Leetcode题目200.岛屿数量（BFS+DFS+并查集-中等）

题目描述：

给定一个由 '1'（陆地）和 '0'（水）组成的的二维网格，计算岛屿的数量。一个岛被水包围，并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。

示例 1:

输入:
11110
11010
11000
00000

输出: 1
示例 2:

输入:
11000
11000
00100
00011

输出: 3

思路分析：题解和示例图来自：liweiwei1419

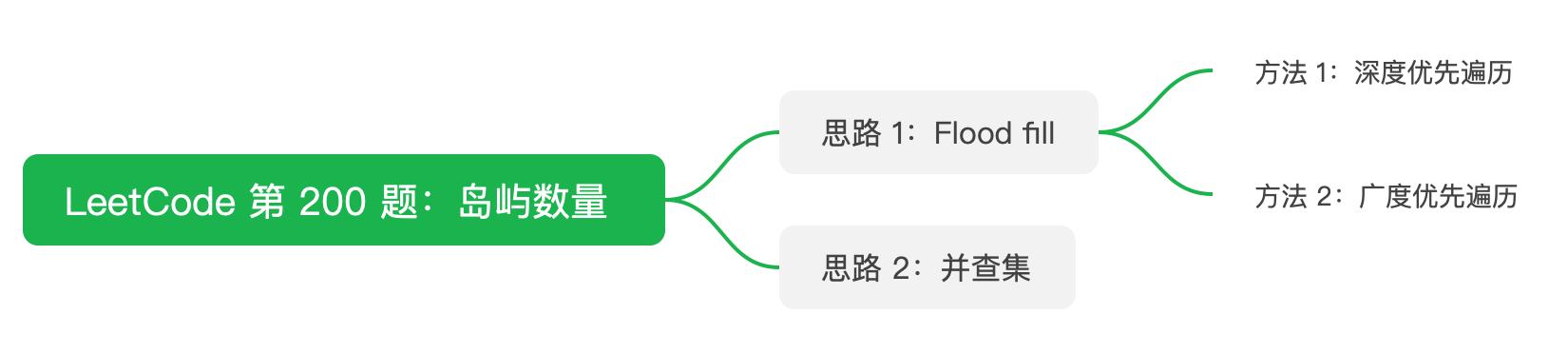
说明：以下介绍的算法，除了并查集以外，DFS 和 BFS 都属于很基础的算法内容，也非常好理解，写法也相对固定，读者需要多写，发现并记录自己的问题，我也是在写了几遍甚至是在写本题解的过程中，才发现出自己的问题。

这道题是可以使用一个经典的算法来解决的，那就是 Flood fill，以下的定义来自 维基百科：Flood fill 词条。

Flood fill 算法是从一个区域中提取若干个连通的点与其他相邻区域区分开（或分别染成不同颜色）的经典 算法。因为其思路类似洪水从一个区域扩散到所有能到达的区域而得名。在 GNU Go 和 扫雷 中，Flood Fill算法被用来计算需要被清除的区域。

“Flood” 我查了一下，作为动词是 “淹没；充满” 的意思，作为名词是 “洪水” 的意思。下面我们简单解释一下这个算法：

从一个区域中提取若干个连通的点与其他相邻区域区分开
从一个点扩散开，找到与其连通的点，这不是什么高深的算法，其实就是从一个点开始，进行一次 “深度优先遍历” 或者 “广度优先遍历”，通过 “深度优先遍历” 或者 “广度优先遍历” 发现一片连着的区域，对于这道题来说，就是从一个是 “陆地” 的格子开始进行一次 “深度优先遍历” 或者 “广度优先遍历”，把与之相连的所有的格子都标记上，视为发现了一个 “岛屿”。

说明：这里做 “标记” 的意思是，通过 “深度优先遍历” 或者 “广度优先遍历” 操作，我发现了一个新的格子，与起始点的那个格子是连通的，我们视为 “标记” 过，也可以说 “被访问过”。

那么每一次进行 “深度优先遍历” 或者 “广度优先遍历” 的条件就是：

1、这个格子是陆地 1，如果是水域 0 就无从谈论 “岛屿”；

2、这个格子不能是之前发现 “岛屿” 的过程中执行了 “深度优先遍历” 或者 “广度优先遍历” 操作，而被标记的格子.

思路一：DFS

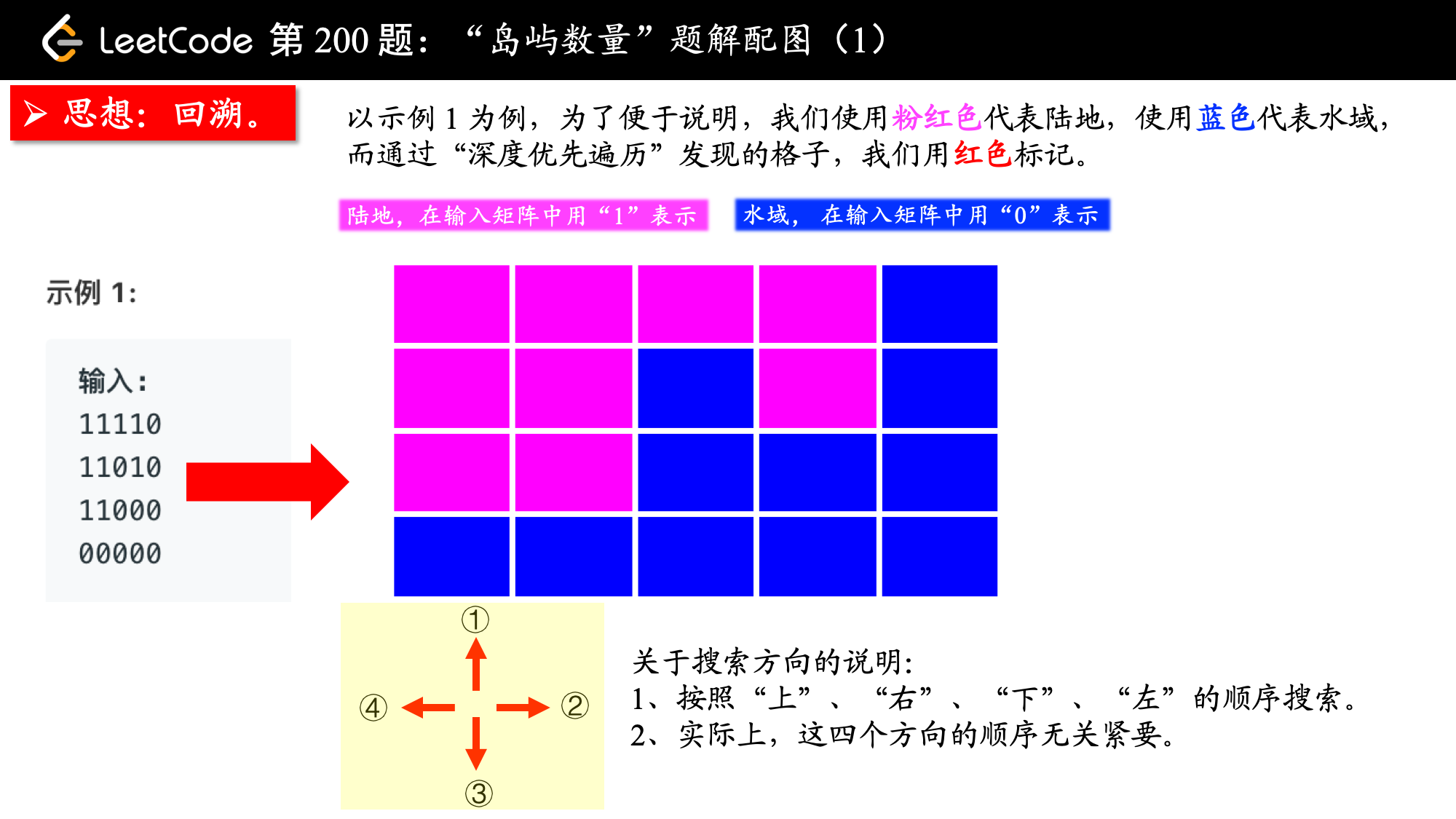
代码实现：

package com.company;

/**
 * @author yaoshw
 */
public class Main {

    public static void main(String[] args) {
        char[][] grid2 = {
                {'1', '1', '0', '0', '0'},
                {'1', '1', '0', '0', '0'},
                {'0', '0', '1', '0', '0'},
                {'0', '0', '0', '1', '1'}};
        System.out.println(numIslands(grid2));

    }

    public static int numIslands(char[][] grid) {

        //grid的行
        int row = grid.length;
        if (row == 0) {
            return 0;
        }
        //grid的列
        int col = grid[0].length;
        //标记grid的处于该坐标的点是否被访问
        boolean[][] visited = new boolean[row][col];
        //表示当前网格的四个方向，上->右->下->左
        int[][] directions = new int[][]{
                {-1, 0}, {0, -1}, {1, 0}, {0, 1}
        };
        //累加找到的岛屿数量
        int count = 0;
        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++) {
                if (grid[i][j] == '1' && !visited[i][j]) {
                    count++;
                    //从当前位置开始深度优先遍历(dfs)
                    dfs(i, j, directions, visited, row, col, grid);
                }
            }
        }
        return count;
    }

    //dfs
    private static void dfs(int i, int j, int[][] directions, boolean[][] visited, int row, int col, char[][] grid) {

        //标记当前节点已经被访问
        visited[i][j] = true;

        //此处k从0~3，表示从一个点到下一个可能的网格，求坐标
        for (int k = 0; k < 4; k++) {
            //下一个要走网格的x坐标
            int newX = i + directions[k][0];
            //下一个要走网格的Y坐标
            int newY = j + directions[k][1];

            //没有走越界，并且没有被访问，并且还是陆地
            if (inArea(newX, newY, row, col) && !visited[newX][newY] && grid[newX][newY] == '1') {
                dfs(newX, newY, directions, visited, row, col, grid);
            }
        }
    }

    //是否越界
    private static boolean inArea(int newX, int newY, int row, int col) {
        return newX >= 0 && newX < row && newY >= 0 && newY < col;
    }
}

思路二：BFS

除了 “深度优先遍历”，你还可以使用 “广度优先遍历”，此时你就不用回溯了。“广度优先遍历” 需要一个 “辅助队列”。

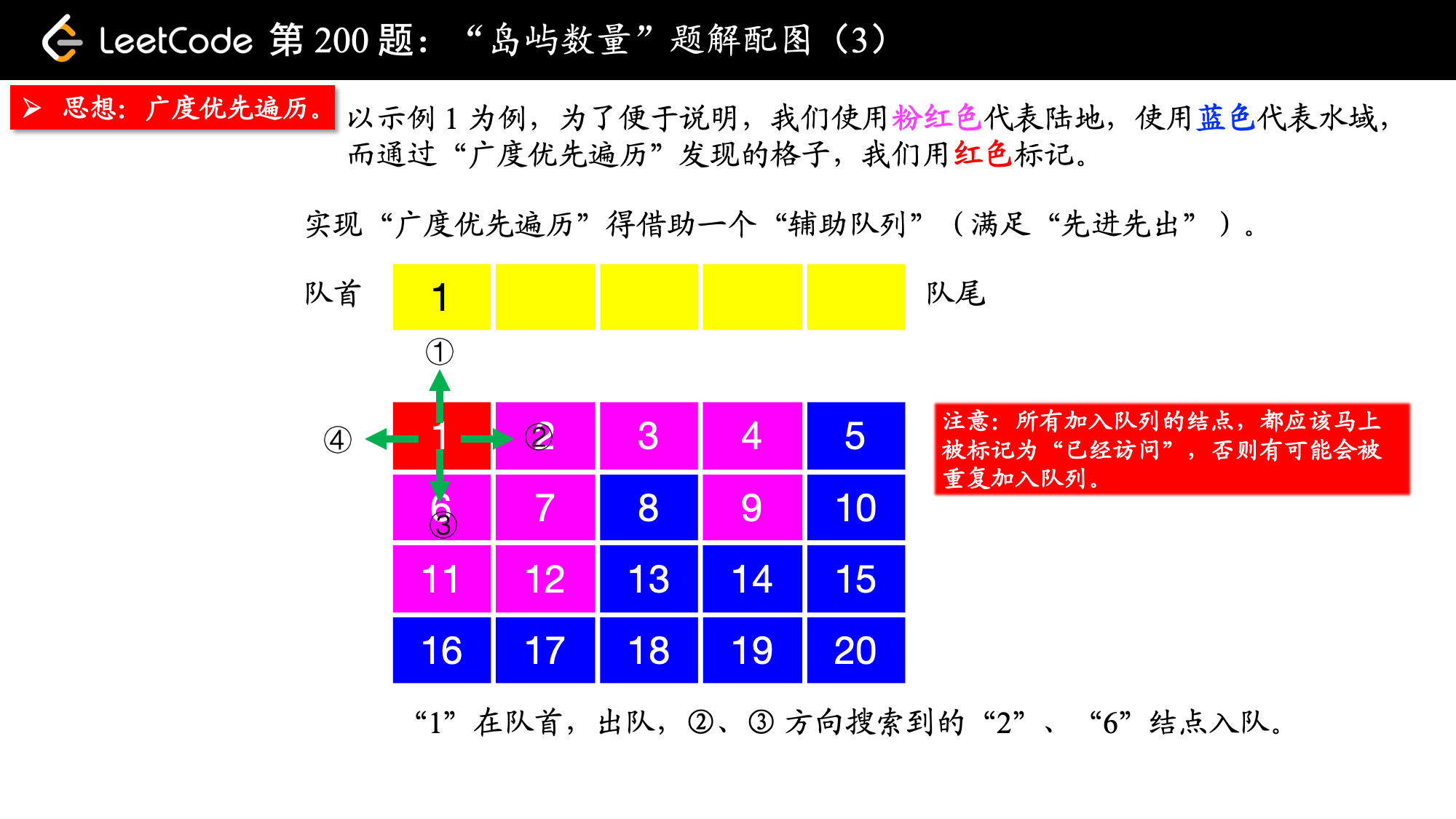
在写 “广度优先遍历” 的时候，要注意一点：所有加入队列的结点，都应该马上被标记为 “已经访问”，否则有可能会被重复加入队列。

代码实现：

/**
 * 方法一：广度优先遍历
 */
public class Solution {

 public static int numIslands(char[][] grid) {

        //grid的行
        int row = grid.length;
        if (row == 0) {
            return 0;
        }
        //grid的列
        int col = grid[0].length;
        //标记grid的处于该坐标的点是否被访问
        boolean[][] visited = new boolean[row][col];
        //表示当前网格的四个方向，上->右->下->左
        int[][] directions = new int[][]{
                {-1, 0}, {0, -1}, {1, 0}, {0, 1}
        };
        //辅助队列
        Deque<Integer> helper = new LinkedList<>();
        //找到的岛屿的数量
        int count = 0;
        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++) {

                // 如果是岛屿中的一个点，并且没有被访问过
                // 从坐标为 (i,j) 的点开始进行广度优先遍历
                if (grid[i][j] == '1' && !visited[i][j]) {

                    count++;
                    //此处有一个小技巧，将坐标->整数，然后加入队列，不然队列中需要放数组
                    helper.addLast(i * col + j);
                    //标记当前节点已经被访问
                    visited[i][j] = true;
                    while (!helper.isEmpty()) {
                        //弹出一个元素
                        int cur = helper.removeFirst();
                        //弹出元素表示的X坐标
                        int curX = cur / col;
                        //弹出元素表示的Y中标
                        int curY = cur % col;
                        //求下一个该走的网格
                        for (int k = 0; k < 4; k++) {
                            int newX = curX + directions[k][0];
                            int newY = curY + directions[k][1];
                            //是网格中的陆地，并且没有被访问，也没有越界
                            if (inArea(newX, newY, row, col) && !visited[newX][newY] && grid[newX][newY] == '1') {
                                //进队列
                                helper.addLast(newX * col + newY);
                                //标记当前节点已经被访问
                                visited[newX][newY] = true;
                            }

                        }

                    }

                }
            }
        }
        return count;
    }

    //是否越界
    private static boolean inArea(int newX, int newY, int row, int col) {
        return newX >= 0 && newX < row && newY >= 0 && newY < col;
    }
}

思路三：并查集

时间复杂度：

空间复杂度：