阶段5 3.微服务项目【学成在线】_day02 CMS前端开发_13-webpack研究-webpack入门程序
创建webpack测试的目录

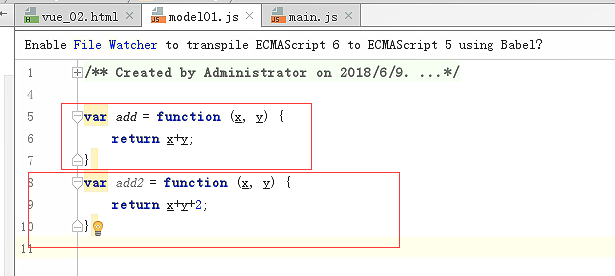
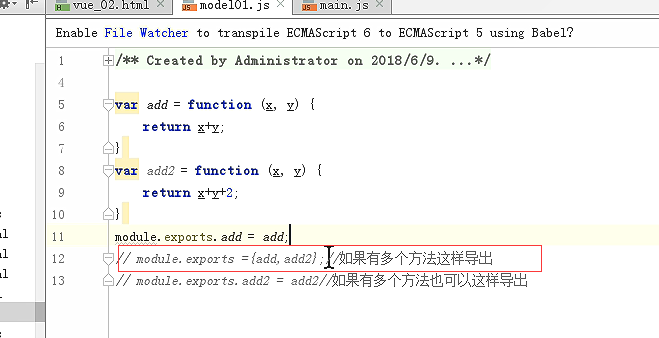
定义webpack的入口文件
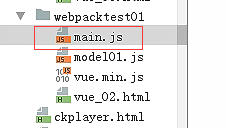
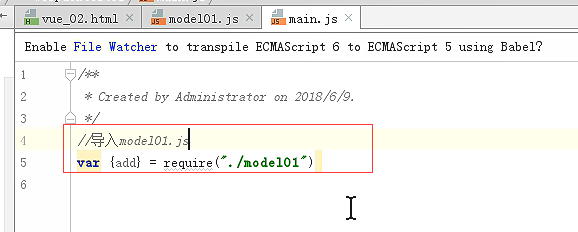
mdel01必须导出,main里面才能导入
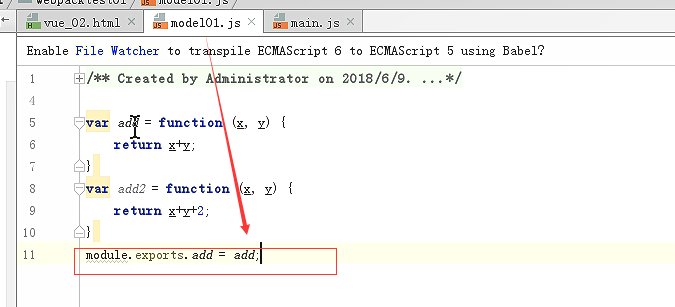
导出多个
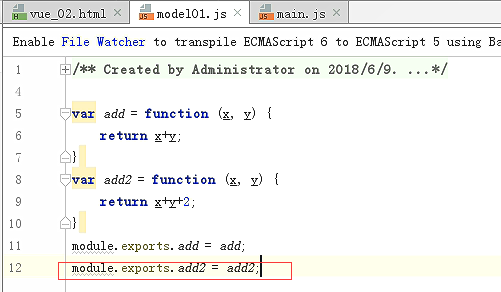
数组的写法
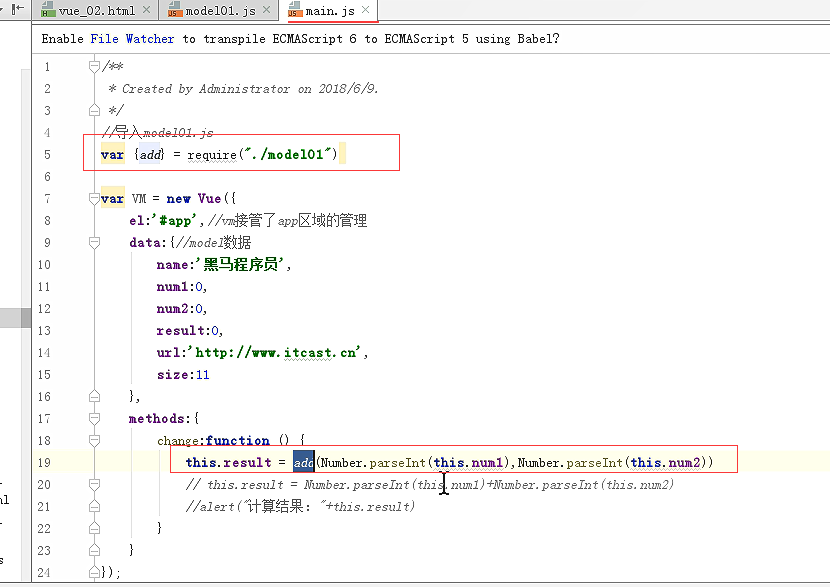
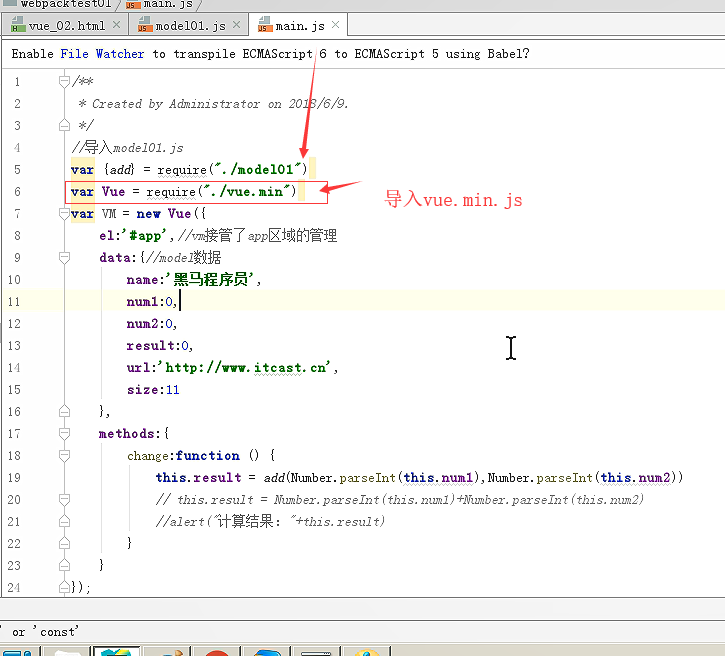
main是入口文件,里面已经引入了vue.min和model01.js


打包生成的文件
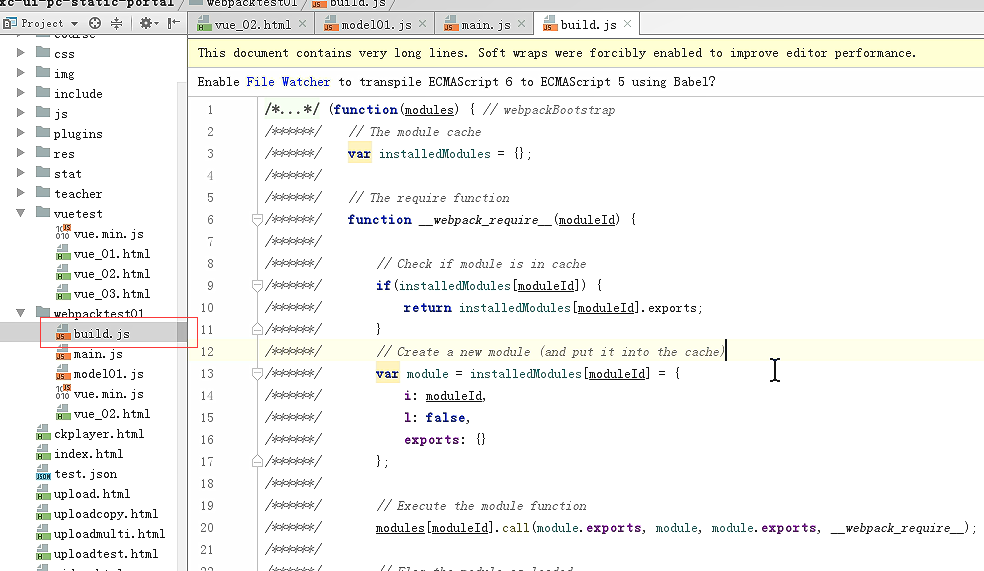
页面最终引用这个build.js
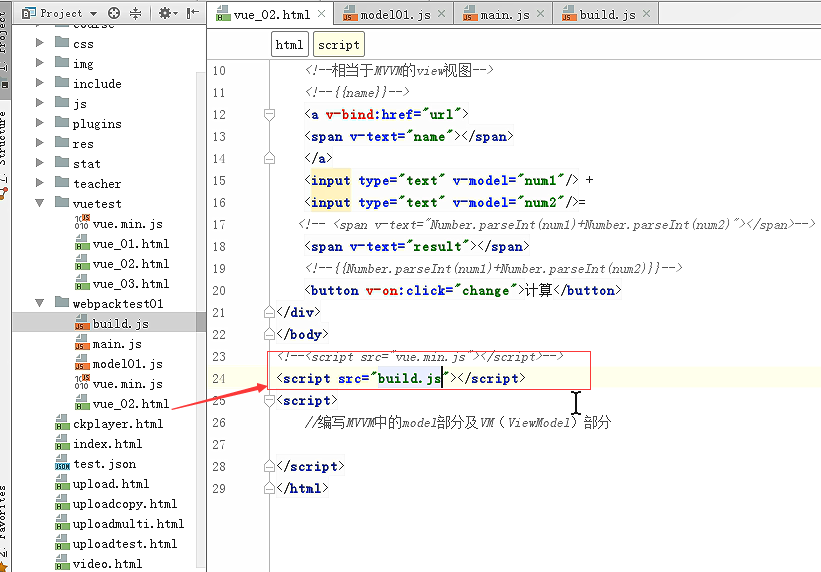
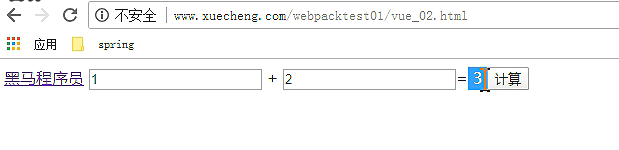
总结

阶段5 3.微服务项目【学成在线】_day02 CMS前端开发_13-webpack研究-webpack入门程序的更多相关文章
- 微服务项目开发学成在线_day02 CMS前端开发
1 Vue.js与Webpack研究 开发版的浏览器:https://www.google.cn/intl/zh-CN/chrome/dev/ 前端的开发框架:微服务项目开发学成在线_Vue.js与W ...
- 阶段5 3.微服务项目【学成在线】_day04 页面静态化_16-页面静态化-模板管理-模板制作
这是轮播图的原始文件 运行门户需要把 nginx启动起来 单独运行轮播图.把里面的css的引用都加上网址的url 这就是单独访问到的轮播图的效果 轮播图模板的地址: 阶段5 3.微服务项目[学成在线] ...
- 阶段5 3.微服务项目【学成在线】_day02 CMS前端开发_16-CMS前端工程创建-导入系统管理前端工程
提供了基于脚手架封装好的前端工程 H:\BaiDu\黑马传智JavaEE57期 2019最新基础+就业+在职加薪\阶段5 3.微服务项目[学成在线]·\day02 CMS前端开发\资料\xc-ui-p ...
- 阶段5 3.微服务项目【学成在线】_day16 Spring Security Oauth2_03-用户认证技术方案-Oauth2协议
2.2 Oauth2认证 2.2.1 Oauth2认证流程 第三方认证技术方案最主要是解决认证协议的通用标准 问题,因为要实现 跨系统认证,各系统之间要遵循一定的 接口协议. OAUTH协议为用户资源 ...
- 阶段5 3.微服务项目【学成在线】_day16 Spring Security Oauth2_01-用户认证需求分析
1.1 用户认证与授权 截至目前,项目已经完成了在线学习功能,用户通过在线学习页面点播视频进行学习.如何去记录学生的学习过程 呢?要想掌握学生的学习情况就需要知道用户的身份信息,记录哪个用户在什么时间 ...
- 阶段5 3.微服务项目【学成在线】_day09 课程预览 Eureka Feign_05-Feign远程调用-客户端负载均衡介绍
2 Feign远程调用 在前后端分离架构中,服务层被拆分成了很多的微服务,服务与服务之间难免发生交互,比如:课程发布需要调用 CMS服务生成课程静态化页面,本节研究微服务远程调用所使用的技术. 下图是 ...
- 阶段5 3.微服务项目【学成在线】_day09 课程预览 Eureka Feign_02-Eureka注册中心-搭建Eureka单机环境
我们先搭建单机环境 govern是治理的意思, 这样就把工程创建好了 创建包 创建SpringBoot的启动类. 在父工程里面已经确定了Spring Cloud的版本了.相当于锁定了版本 接下里只需要 ...
- 阶段5 3.微服务项目【学成在线】_day09 课程预览 Eureka Feign_04-Eureka注册中心-将服务注册到Eureka Server
cms相当于客户端 配置客户端的信息 后面加逗号分隔开 50102表示向两台eureka服务上报服务,如果有一台死掉了 那么还可以上另外的一台去注册服务 直接把ip注册到eureka 启动类加注解 重 ...
- 阶段5 3.微服务项目【学成在线】_day09 课程预览 Eureka Feign_01-Eureka注册中心-Eureka介绍
1 Eureka注册中心 1.1 需求分析 在前后端分离架构中,服务层被拆分成了很多的微服务,微服务的信息如何管理?Spring Cloud中提供服务注册中 心来管理微服务信息. 为什么 要用注册中心 ...
- 阶段5 3.微服务项目【学成在线】_day18 用户授权_03-方法授权-jwt令牌包含权限
修改认证服务的UserDetailServiceImpl类,下边的代码中 permissionList列表中存放了用户的权限, 并且将权限标识按照中间使用逗号分隔的语法组成一个字符串,最终提供给Spr ...
随机推荐
- IBM XIV
参考:https://www.doit.com.cn/p/author/xigua 参考:http://www.doit.com.cn/p/196056.html 图片说明: IBM XIV存储系统采 ...
- 2018江苏徐州icpc试题-A-生化危机【多源点-基础广搜】
- git ls-files 列出被修改或者被删除的文件
git ls-files 列出被修改或者被删除的文件 git ls-files -m -d
- JAVA遇见HTML——JSP篇(JSP内置对象下)
request.getSession() 网上资料解释: request只能存在于一次访问里 session对象的作用域为一次会话 session长驻在服务器内存里,session有id标识,一个se ...
- Lua 学习之基础篇六<Lua IO 库>
引言 I/O 库提供了两套不同风格的文件处理接口. 第一种风格使用隐式的文件句柄: 它提供设置默认输入文件及默认输出文件的操作, 所有的输入输出操作都针对这些默认文件. 第二种风格使用显式的文件句柄. ...
- tp5.1下redis配置和使用
//1.config目录下新建redis.php <?php /** * Created by PhpStorm. * User: Administrator * Date: 2019/12/1 ...
- Java8-Lambda-No.04
public class Lambda4 { static int outerStaticNum; int outerNum; void testScopes() { int num = 1; Lam ...
- javascript逻辑或(||)
<!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...
- GET 和 POST is so different
.原理区别 一般我们在浏览器输入一个网址访问网站都是GET请求;再FORM表单中,可以通过设置Method指定提交方式为GET或者POST提交方式,默认为GET提交方式. HTTP定义了与服务器交互的 ...
- 001_FreeRTOS中断配置
(一)优先级看:022_STM32中断优先级分组解析 (二)FreeRTOS的中断配置中没有处理亚优先级(响应优先级)的情况,所以只能配置成组4,16个都为抢占优先级 (三)此宏用来设置 MCU 使用 ...
