CTR@因子分解机(FM)

1. FM算法

　　FM（Factor Machine，因子分解机）算法是一种基于矩阵分解的机器学习算法，为了解决大规模稀疏数据中的特征组合问题。FM算法是推荐领域被验证效果较好的推荐算法之一，在电商、广告、直播等推荐领域有广泛应用。

2. FM算法优势

　　特征组合：通过对两两特征组合，引入交叉项特征。

　　解决维数灾难：通过引入隐向量，实现对特征的参数估计。

3. FM表达式

　　对于度为2的因子分解机FM的模型为：

其中，参数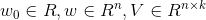。 aaarticlea/gif;base64,R0lGODlhMAAUALMAAP///wAAAHZ2du7u7kRERIiIiKqqqjIyMszMzGZmZpiYmNzc3FRUVLq6uhAQECIiIiH5BAEAAAAALAAAAAAwABQAAATdEEghq704a0vvIFsobsxyFcaork1XHWs8whWSyLhWNFWC5EDLgPGyNBQ3wMBhUh2Ty2aGMAAYFJUB1vEDHHgjLYAr+W6uAGqFtwhUCk2DC8N2S+CWxwVE4xAlWBJVIgJ/AIEVUmUAAl0VDymAMpAViBkLRAtJFQGDCE0FhhudEp+VjRxdIBakh5IPg5iDrIOIBgNyFn0KkRIGCQqWC30IDpa+wJZVCb0NBVmrIQLHvSoHUgyzACUisJbVIw7QFy2EeHfaIgjRKBh9K+AiBc+LGIpBGhTXifhABLwbIgAAOw==" alt="" />表示的是两个大小为aaarticlea/gif;base64,R0lGODlhCQANALMAAP///wAAAHZ2du7u7szMzDIyMhAQEKqqqlRUVJiYmNzc3Lq6ukRERIiIiCIiIgAAACH5BAEAAAAALAAAAAAJAA0AAAQyEEgxpCXF2H3QtkjySYYyKhpwJB7AusOSMs0xBsVRXRpRWo2Ww7YAFEQAByGW3CUEyAgAOw==" alt="" />的向量aaarticlea/gif;base64,R0lGODlhDQALALMAAP///wAAALq6upiYmGZmZu7u7hAQENzc3MzMzDIyMoiIiHZ2dlRUVCIiIqqqqgAAACH5BAEAAAAALAAAAAANAAsAAAQ6EIhBACjmWFsGMIiVCJsEHMGmaICzWAuzedzWOHO5BYWFsAqZhWeheRq9FmFAsxwSuuiiGbUgqdJVBAA7" alt="" />和向量aaarticlea/gif;base64,R0lGODlhDwAOALMAAP///wAAALq6upiYmGZmZu7u7hAQENzc3MzMzDIyMoiIiHZ2dlRUVCIiIqqqqkRERCH5BAEAAAAALAAAAAAPAA4AAARLEIhBACjm2H0HMIiVCJxFHsGmaFuzLczmcSzQOHLJBYWF1INFyMKzzACOgmOxcRAGxwuAgNPpEjXrxqAtIR5djkIRBjCx5cegCogAADs=" alt="" />的点积：

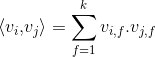
其中，aaarticlea/gif;base64,R0lGODlhDQALALMAAP///wAAALq6upiYmGZmZu7u7hAQENzc3MzMzDIyMoiIiHZ2dlRUVCIiIqqqqgAAACH5BAEAAAAALAAAAAANAAsAAAQ6EIhBACjmWFsGMIiVCJsEHMGmaICzWAuzedzWOHO5BYWFsAqZhWeheRq9FmFAsxwSuuiiGbUgqdJVBAA7" alt="" />表示的是系数矩阵aaarticlea/gif;base64,R0lGODlhDgAMALMAAP///wAAAHZ2dhAQEGZmZszMzJiYmDIyMqqqqoiIiO7u7rq6ulRUVAAAAAAAAAAAACH5BAEAAAAALAAAAAAOAAwAAAQ7EIgRSAEYmHAQTkGWKYSIBIoIJGoRXNkCj4GHKawKBEKW6wcGRqbDMA4AXBEzkSwxG8OsuAj8lgrkMgIAOw==" alt="" />的第aaarticlea/gif;base64,R0lGODlhBgANALMAAP///wAAAKqqqhAQEO7u7tzc3Lq6upiYmGZmZszMzHZ2diIiIoiIiAAAAAAAAAAAACH5BAEAAAAALAAAAAAGAA0AAAQiEMg5xaCk0L3NQRJxAEMCGEARUAo4ldVySooCMFKCHAQQAQA7" alt="" />维向量，且aaarticlea/gif;base64,R0lGODlh5gAWALMAAP///wAAALq6upiYmGZmZu7u7hAQENzc3MzMzDIyMoiIiHZ2dlRUVCIiIqqqqkRERCH5BAEAAAAALAAAAADmABYAAAT+EMhJq7046827/2AojmRpnmiqrmw7IoILFoNs3+FQ4LLg8BsCcEicFISfxa548TErCsRzahMoOoiEQbZoBKSSAiPw+FGcVEAizWatOw6GTdGQU5CAI4HweOwJB0wDNW2FJwpmGwyEHAcLfX1XGgMKAUt5iWeZTA+Bhp8vdhsGnhsDD2AdAgcFAZIADpeaFQIDSAWkMltntmG5J7W3v2zBvqUguxoHuw4DorR4HpIEya+0mTQABmAJMS7JeTXbEt0n2eNq3mnn3OogARzOADoC4BRvIJIIAd7WsxMxDsCToMCTgwUXCDBYyLAhQgsHGpwBIHBCQQkHIT7YEHAggIv+sB5OcKBgQbQWHS0aFBnmgT8JDWRdcLkJIssO2chtPOCugkwAC0Qx+lkiooWgE4ZaGNClA1IJSikUkMTgZoun84xcYNATJlEKARLE0iCgAaSzLwGWchDgACMPDRK9XYHLQtykG4xyuAs1g4A3A/DJ4JtVg8QL9iwg2LL4WIUDJ+NVMLAgrQZLEhB4UvDsTsPPVTEkxgxAM8HOEvRuIG36I2pPJnGw3vx6zUF3iaHYuduVXI4KCwxYzkCaUI2YKzpVKN4X+ePDqRn8ZJ7VuV1PB6Q/1k6Re/Yl3y1QPy7TAQEdUSYgEBX+HqEGCAr0Lo06A4K5reZnMD+IwgHBKPTcRwF/b/13gWqlGTAXLOcVCOAEXKmnYAWLgVFhZugstiCB/j1ITU2ISDiXc0wtOGAZjllATQNzRUbCAiaWUMBGHMB4IHQjeWCjBekdUxMIP16wIwUxVVbBg0F+QAMfkVARU4wvppLBkwAIcAmCGMGVjZUYxXKANUnCoWUNXBYg0UGt1WJBmKA4BdIKLgJ3kUsSCECAK6Uo8NVRc14hUACAiqRnCYO6GQidCAhxBCFH8Lhnm2zk5EGYbO6nQaWXkpCkDmtC6qkIBWAaQqiekvrpqTKIGoKqRbCK6gYRAAA7" alt="" />称为超参数。在因子分解机FM模型中，前面两部分是传统的线性模型，最后一部分将两个互异特征分量之间的交叉关系考虑进来。

　　因子分解机也可以推广到高阶的形式，即将更多互异特征分量之间的相互关系考虑进来。

4. 交叉项

　　　　

　　算法核心为交叉项计算，可以明显降低模型时间复杂度，现在模型的复杂度为。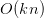

5. 求解问题

　　FM算法主要可以处理三类问题：回归问题、二分类问题、排序。

　　5.1 回归问题

　　　　在回归问题中，直接使用aaarticlea/gif;base64,R0lGODlhDAASALMAAP///wAAALq6uqqqqtzc3ERERDIyMszMzO7u7nZ2dlRUVGZmZoiIiJiYmBAQECIiIiH5BAEAAAAALAAAAAAMABIAAARREEgpxryAFLPPRYniZcuCSAyBAQhzrnA8HcMyDcqENIAzKomJIBOYOIaXkORQxDwsAIZhFXgVgpgqEXlpJLzaGKOwOkoeXAnCBkiwMQ0vbxUBADs=" alt="" />作为最终的预测结果。在回归问题中使用最小均方误差作为优化标准，即

　　　　

其中，aaarticlea/gif;base64,R0lGODlhEAAIALMAAP///wAAAJiYmIiIiO7u7lRUVLq6uszMzNzc3KqqqiIiIkRERHZ2dmZmZhAQEDIyMiH5BAEAAAAALAAAAAAQAAgAAAQ/EIgxiBDFWHwAIAYSCF6ikNLiGYDpScrLFC/QMG+BewvqOaxfkBBAvETHwEvwAASZS5WnMQBUAQxf9nVgVAARADs=" alt="" />表示样本的个数。

　　5.2 二分类问题

　　　　在二分类问题中使用Logitloss作为优化标准，即

其中，aaarticlea/gif;base64,R0lGODlhCwAIALMAAP///wAAAJiYmCIiIhAQEFRUVGZmZu7u7kRERHZ2drq6ujIyMszMzKqqqtzc3AAAACH5BAEAAAAALAAAAAALAAgAAAQoEEgxgg1EgmLOQYkGCIimLCLBaE0pOZlmhNKZHuKgFY0IMAlBYiWKAAA7" alt="" />表示的是阶跃函数Sigmoid，其数学表达式为：

6. FM&SVM

　　SVM的二元特征交叉参数是独立的，而FM的二元特征交叉参数是两个维的向量，交叉参数并不独立，两者相互影响。

　　FM可以在原始形式下进行优化学习，而基于核的非线性SVM通常需要在对偶形式下优化学习。

　　FM的模型预测与训练样本独立，而SVM则与训练样本有关（支持向量）。

7. 交叉项核心代码

 v = normalvariate(0, 0.2) * ones((n, k))    #初始化隐向量
 inter_1 = dataMatrix[x] * v
 inter_2 = multiply(dataMatrix[x], dataMatrix[x]) * multiply(v, v)   #multiply对应元素相乘
 interaction = sum(multiply(inter_1, inter_1) - inter_2) / 2.    #完成交叉项
 p = w_0 + dataMatrix[x] * w + interaction   #计算预测的输出

Time : 2019-10-14 09:39:44