LeetCode 1105. Filling Bookcase Shelves

原题链接在这里：https://leetcode.com/problems/filling-bookcase-shelves/

题目：

We have a sequence of books: the i-th book has thickness books[i][0] and height books[i][1].

We want to place these books in order onto bookcase shelves that have total width shelf_width.

We choose some of the books to place on this shelf (such that the sum of their thickness is <= shelf_width), then build another level of shelf of the bookcase so that the total height of the bookcase has increased by the maximum height of the books we just put down.  We repeat this process until there are no more books to place.

Note again that at each step of the above process, the order of the books we place is the same order as the given sequence of books.  For example, if we have an ordered list of 5 books, we might place the first and second book onto the first shelf, the third book on the second shelf, and the fourth and fifth book on the last shelf.

Return the minimum possible height that the total bookshelf can be after placing shelves in this manner.

Example 1:

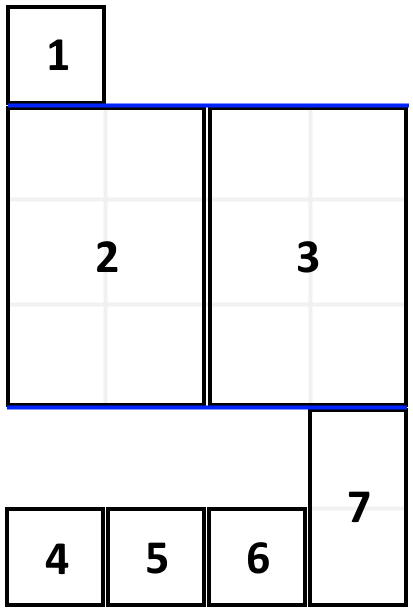
Input: books = [[1,1],[2,3],[2,3],[1,1],[1,1],[1,1],[1,2]], shelf_width = 4
Output: 6
Explanation:
The sum of the heights of the 3 shelves are 1 + 3 + 2 = 6.
Notice that book number 2 does not have to be on the first shelf.

Constraints:

• 1 <= books.length <= 1000
• 1 <= books[i][0] <= shelf_width <= 1000
• 1 <= books[i][1] <= 1000

题解：

Let dp[i] denotes up to index i-1, the minimum height.

For the new book i. It could be on the next row. It could be just itself or with previous books.

When book i and previous i-1, i-2 ... j, stay on the same row, its total width could not be larger than shelf_width.

And coming to j, it could be like j to i-1 is already on this row, i is just added to the same row.

For each j < i, util total width <= shelf_width, update dp[i] with dp[j-1] + max(book j, j+1, j+2, ... i). When update it uses dp[j-1], since j is already on the next row.

Time Complexity: O(n^2). n = books.length.

Space: O(n).

AC Java:

 class Solution {
     public int minHeightShelves(int[][] books, int shelf_width) {
         if(books == null || books.length == 0 || shelf_width <= 0){
             return 0;
         }

         int n = books.length;
         int [] dp = new int[n+1];

         for(int i = 1; i<=n; i++){
             int w = books[i-1][0];
             int h = books[i-1][1];
             dp[i] = dp[i-1] + h;
             for(int j = i-1; j>0 && w+books[j-1][0]<=shelf_width; j--){
                 h = Math.max(h, books[j-1][1]);
                 w += books[j-1][0];
                 dp[i] = Math.min(dp[i], dp[j-1]+h);
             }
         }

         return dp[n];
     }
 }