bzoj 2753 [SCOI 2012] 滑雪与时间胶囊 - Prim

题目传送门

　　传送点I

　　传送点II

题目大意

　　给定一个有$n$个点$m$条边的图，每个点有一个高度$h_{i}$，能从$u$经过一条边到达$v$，当且仅当存在一条边是$(u, v)$或$(v, u)$，且$h_{u}\geqslant h_{v}$。问1号点能到达的所有点的最小树形图的边权和。

　　第一问沙雕问题。直接一个搜索水过。

　　第二问，好像是最小树形图。看着数据范围，嗯，别想朱-刘了。

　　感觉可以直接Prim。于是愉快地WA了一发。来回顾一下Prim算法的正确性证明

可以不妨设图中所有边的权重都不同，这样最小生成树是唯一的

设Prim算法得到$G$，而最小生成树是$T$。考虑用反证法。

设在生成G的过程中第一次产生的不在T中的边是$e$，未加入$e$时的点集为$V$。

把$e$加入$T$之后会出现环，这个环内必然存在一条边$f = (u, v) \neq e$使得$u\in V, v\notin V$（因为$e$的一个端点不在$V$中）。由Prim的贪心策略可知$w(e) < w(f)$。用$e$替换掉$f$可以得到更优的生成树，这与最小生成树矛盾。因此$T = G$。

　　但树形图不像树那么简单。如果尝试用这种方法去证明可以发现需要讨论两条边的方向，于是很轻松就能卡掉这个zz做法。

　　然后如何hack这个zz做法呢？

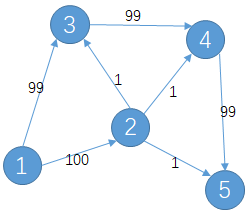
　　于是这个假做法跑出了497的优秀答案。

　　好了好了，开始说正题。

　　因为不能用朱-刘算法，考虑这样的图有什么样的性质。

　　把通过双向边连通的点缩起来。这样剩一个DAG。

　　考虑对于一个被缩起来的一块，它自己相当于一个无向图，可以用最小生成树的算法。

　　对于连向这个块的出边，它们选还是不选入树形图只对这个块中的选边有影响。

　　因此可以将前面的块都看成一个点。然后很有趣的事情来了，直接把这些有向边看成无向边，然后上MST算法。

　　为什么这样做是对的。因为我们可以将任意一个树形图映射成一个边权和与它相等的生成树或者一个生成树映射成一个边权和与它相等的树形图。

　　做法很简单。前一部分直接将有向边看成无向边，后一部分从 "前面的块都看成一个点" 指的点开始沿着树边bfs，这样就可以定向了。

　　具体实现不用将前面的块缩起来。直接以结束点的高度为第一关键字，边权为第二关键字排序即可。

　　（虽然我很好奇为什么大家都写Kruskal。显然写Prim可以少写点东西）

Code

 /**
  * bzoj
  * Problem#
  * Accepted
  * Time: 13128ms
  * Memory: 53364k
  */
 #include <bits/stdc++.h>
 #ifndef WIN32
 #define Auto "%lld"
 #else
 #define Auto "%I64d"
 #endif
 using namespace std;
 typedef bool boolean;

 typedef class Edge {
     public:
         int ed, w;

         Edge() {    }
         Edge(int ed, int w):ed(ed), w(w) {    }
 }Edge;

 int n, m;
 int *hs;
 boolean* added;
 vector<Edge> *g;

 boolean operator < (const Edge& a, const Edge& b) {
     if (hs[a.ed] ^ hs[b.ed])    return hs[a.ed] < hs[b.ed];
     return a.w > b.w;
 }

 inline void init() {
     scanf("%d%d", &n, &m);
     hs = new int[(n + )];
     added = new boolean[(n + )];
     g = new vector<Edge>[(n + )];
     memset(added, false, sizeof(boolean) * (n + ));
     for (int i = ; i <= n; i++)
         scanf("%d", hs + i);
     for (int i = , u, v, w; i <= m; i++) {
         scanf("%d%d%d", &u, &v, &w);
         if (hs[u] >= hs[v])
             g[u].push_back(Edge(v, w));
         if (hs[u] <= hs[v])
             g[v].push_back(Edge(u, w));
     }
 }

 int rc = ;
 long long rv = ;
 priority_queue<Edge> que;
 inline void solve() {
     added[] = true;
     for (int i = ; i < (signed) g[].size(); i++)
         que.push(g[][i]);
     while (!que.empty()) {
         while (!que.empty() && added[que.top().ed])
             que.pop();
         if (que.empty())
             break;
         Edge e = que.top();
         que.pop();
         added[e.ed] = true, rc++, rv += e.w;
         for (int i = ; i < (signed) g[e.ed].size(); i++)
             que.push(g[e.ed][i]);
     }
     printf("%d "Auto, rc, rv);
 }

 int main() {
     init();
     solve();
     return ;
 }