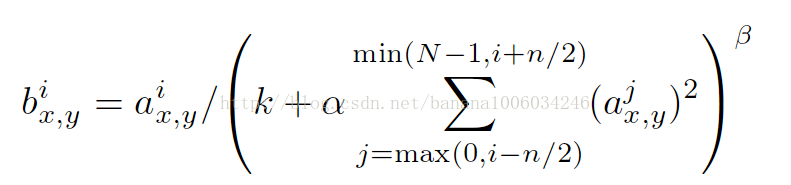LRN（local response normalization--局部响应标准化）

LRN全称为Local Response Normalization，即局部响应归一化层，LRN函数类似DROPOUT和数据增强作为relu激励之后防止数据过拟合而提出的一种处理方法。这个函数很少使用，基本上被类似DROPOUT这样的方法取代，见最早的出处AlexNet论文对它的定义, 《ImageNet Classification with Deep ConvolutionalNeural Networks》

i：代表下标，你要计算像素值的下标，从0计算起

j：平方累加索引，代表从j～i的像素值平方求和

x,y：像素的位置，公式中用不到

a：代表feature map里面的 i 对应像素的具体值

N：每个feature map里面最内层向量的列数

k：超参数，由原型中的blas指定

α：超参数，由原型中的alpha指定

n/2：超参数，由原型中的deepth_radius指定

β：超参数，由原型中的belta指定

背景知识： 

tensorflow官方文档中的tf.nn.lrn函数给出了局部响应归一化的论文出处 ，详见http://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks

为什么要有局部响应归一化（Local Response Normalization）？详见http://blog.csdn.net/hduxiejun/article/details/70570086

tensorflow中调用：

看一个栗子，理解上诉的参数，进而理解rln函数

import tensorflow as tf  

a = tf.constant([
    [[1.0, 2.0, 3.0, 4.0],
     [5.0, 6.0, 7.0, 8.0],
     [8.0, 7.0, 6.0, 5.0],
     [4.0, 3.0, 2.0, 1.0]],
    [[4.0, 3.0, 2.0, 1.0],
     [8.0, 7.0, 6.0, 5.0],
     [1.0, 2.0, 3.0, 4.0],
     [5.0, 6.0, 7.0, 8.0]]
])
#reshape 1批次  2x2x8的feature map
a = tf.reshape(a, [1, 2, 2, 8])  

normal_a=tf.nn.lrn(a,2,0,1,1)
with tf.Session() as sess:
    print("feature map:")
    image = sess.run(a)
    print (image)
    print("normalized feature map:")
    normal = sess.run(normal_a)
    print (normal)

你将得到输出：

    feature map:
    [[[[ 1.  2.  3.  4.  5.  6.  7.  8.]
       [ 8.  7.  6.  5.  4.  3.  2.  1.]]  

      [[ 4.  3.  2.  1.  8.  7.  6.  5.]
       [ 1.  2.  3.  4.  5.  6.  7.  8.]]]]
    normalized feature map:
    [[[[ 0.07142857  0.06666667  0.05454545  0.04444445  0.03703704  0.03157895
         0.04022989  0.05369128]
       [ 0.05369128  0.04022989  0.03157895  0.03703704  0.04444445  0.05454545
         0.06666667  0.07142857]]  

      [[ 0.13793103  0.10000001  0.0212766   0.00787402  0.05194805  0.04
         0.03448276  0.04545454]
       [ 0.07142857  0.06666667  0.05454545  0.04444445  0.03703704  0.03157895
         0.04022989  0.05369128]]]] 

分析如下：

由调用关系得出 n/2=2，k=0，α=1，β=1，N=8

第一行第一个数来说：i = 0

a = 1，min(N-1, i+n/2) = min(7, 2)=2，j = max(0, i - k)=max(0, 0)=0，下标从0~2个数平方求和， b=1/(1^2 + 2^2 + 3^2)=1/14 = 0.071428571

同理，第一行第四个数来说：i = 3

a = 4，min(N-1, i+n/2) = min(7, 5 )=5, j = max(0,1) = 1，下标从1~5进行平方求和，b = 4/(2^2 + 3^2 + 4^2 + 5^2 + 6^2) = 4/90=0.044444444

再来一个，第二行第一个数来说： i = 0

a = 8, min(N-1, i+n/2) = min(7, 2) = 2, j=max(0,0)=0, 下标从0~2的3个数平方求和，b = 8/(8^2 + 7^2 + 6^2)=8/149=0.053691275

其他的也是类似操作

ps：

1、AlexNet将LeNet的思想发扬光大，把CNN的基本原理应用到了很深很宽的网络中。AlexNet主要使用到的新技术点如下：

（1）成功使用ReLU作为CNN的激活函数，并验证其效果在较深的网络超过了Sigmoid，成功解决了Sigmoid在网络较深时的梯度弥散问题。虽然ReLU激活函数在很久之前就被提出了，但是直到AlexNet的出现才将其发扬光大。

（2）训练时使用Dropout随机忽略一部分神经元，以避免模型过拟合。Dropout虽有单独的论文论述，但是AlexNet将其实用化，通过实践证实了它的效果。在AlexNet中主要是最后几个全连接层使用了Dropout。

（3）在CNN中使用重叠的最大池化。此前CNN中普遍使用平均池化，AlexNet全部使用最大池化，避免平均池化的模糊化效果。并且AlexNet中提出让步长比池化核的尺寸小，这样池化层的输出之间会有重叠和覆盖，提升了特征的丰富性。

（4）提出了LRN层，对局部神经元的活动创建竞争机制，使得其中响应比较大的值变得相对更大，并抑制其他反馈较小的神经元，增强了模型的泛化能力。

2、为什么输入数据需要归一化（Normalized Data）？

归一化后有什么好处呢？原因在于神经网络学习过程本质就是为了学习数据分布，一旦训练数据与测试数据的分布不同，那么网络的泛化能力也大大降低；另外一方面，一旦每批训练数据的分布各不相同(batch 梯度下降)，那么网络就要在每次迭代都去学习适应不同的分布，这样将会大大降低网络的训练速度，这也正是为什么我们需要对数据都要做一个归一化预处理的原因。

对于深度网络的训练是一个复杂的过程，只要网络的前面几层发生微小的改变，那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变，那么这一层网络就需要去适应学习这个新的数据分布，所以如果训练过程中，训练数据的分布一直在发生变化，那么将会影响网络的训练速度。

参考文献：

https://blog.csdn.net/banana1006034246/article/details/75204013

https://blog.csdn.net/u011204487/article/details/76026537

https://blog.csdn.net/yangdashi888/article/details/77918311