triangular distribution

mode(众数)，

一组数据中出现次数最多的那个(或那些)数值。

众数可以不存在或多于一个。

例如，

1，2，3，3，4的众数是3。

1，2，2，3，3，4的众数是2和3。

1，2，3，4，5没有众数。(所有数据出现的次数都一样)

用众数代表一组数据，可靠性较差，但众数不受极端数据的影响。

当数值或被观察者没有明显次序(如非数值性资料)时，无法求平均值和中位数，这时众数就特别有用。例如，{鸡、鸭、鱼、鱼、鸡、鱼}的众数是鱼。

进入正题，

三角分布，亦称辛普森分布或三角形分布。在概率论与统计学中，三角形分布是低限为a、众数为c、上限为b的连续概率分布。

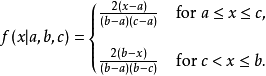
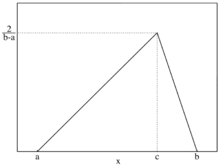
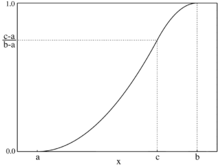累计分布