crontab[计划任务]，tar[压缩]，grep[查找]

计划任务：
1.新建一个计划任务：crontab -e -----> 3
*/1 * * * * date >> /tmp/data.txt
查看计划任务：crontab -l
.如果超过64个字节，写到文件里面---->如下：
cd /tmp
vim crontab.sh
=====#!/bash/bin
=====date >> /tmp/data.txt

如果没有写#!/bash/bin,则计划任务如下这样写：
*/1 * * * * /bin/bash /tmp/crontab.sh

如果写了#!/bash/bin,则计划任务如下这样写：
*/1 * * * * . /tmp/crontab.sh

用cat /tmp/data.txt 查看
-----------------------------------------------------
* * * * * command to be executed
- - - - - -
| | | | | |
| | | | | --- 预执行的命令
| | | | ----- 表示星期0～7（其中星期天可以用0或7表示）
| | | ------- 表示月份1～12
| | --------- 表示日期1～31
| ----------- 表示小时1～23（0表示0点）
------------- 表示分钟1～59 每分钟用*或者 */1表示

-u user：用来设定某个用户的crontab服务；
-e：编辑某个用户的crontab文件内容。如果不指定用户，则表示编辑当前用户的crontab文件。
-l：显示某个用户的crontab文件内容，如果不指定用户，则表示显示当前用户的crontab文件内容。
-r：从/var/spool/cron目录中删除某个用户的crontab文件，如果不指定用户，则默认删除当前用户的crontab文件。
-i：在删除用户的crontab文件时给确认提示
2.tar 压缩

-c ：建立一个压缩文件的参数指令(create 的意思)；
-x ：解开一个压缩文件的参数指令！
-t ：查看 tarfile 里面的文件！
特别注意  c/x/t 同时仅能存在一个，因为不可能同时压缩与解压缩。
-z ：是否同时具有 gzip 的属性？亦即是否需要用 gzip 压缩？
-j ：是否同时具有 bzip2 的属性？亦即是否需要用 bzip2 压缩？
-v ：压缩的过程中显示文件！这个常用，但不建议用在背景执行过程！
-f ：使用档名，请留意，在 f 之后要立即接文件名
-p ：使用原文件的原来属性（属性不会依据使用者而变）
-P ：可以使用绝对路径来压缩！
-N ：比后面接的日期(yyyy/mm/dd)还要新的才会被打包进新建的文件中！

# 将当前目录下所有.txt文件打包并压缩归档到文件this.tar.gz
tar czvf this.tar.gz ./*.txt
# 将当前目录下的this.tar.gz中的文件解压到当前目录
tar xzvf this.tar.gz ./

# 将整个 /etc 目录下的文件全部打包成为 /tmp/etc.tar
tar -cvf /tmp/etc.tar /etc  # 仅打包，不压缩！
tar -zcvf /tmp/etc.tar.gz /etc  # 打包后，以 gzip 压缩
tar -jcvf /tmp/etc.tar.bz2 /etc  # 打包后，以 bzip2 压缩

# 解压文件
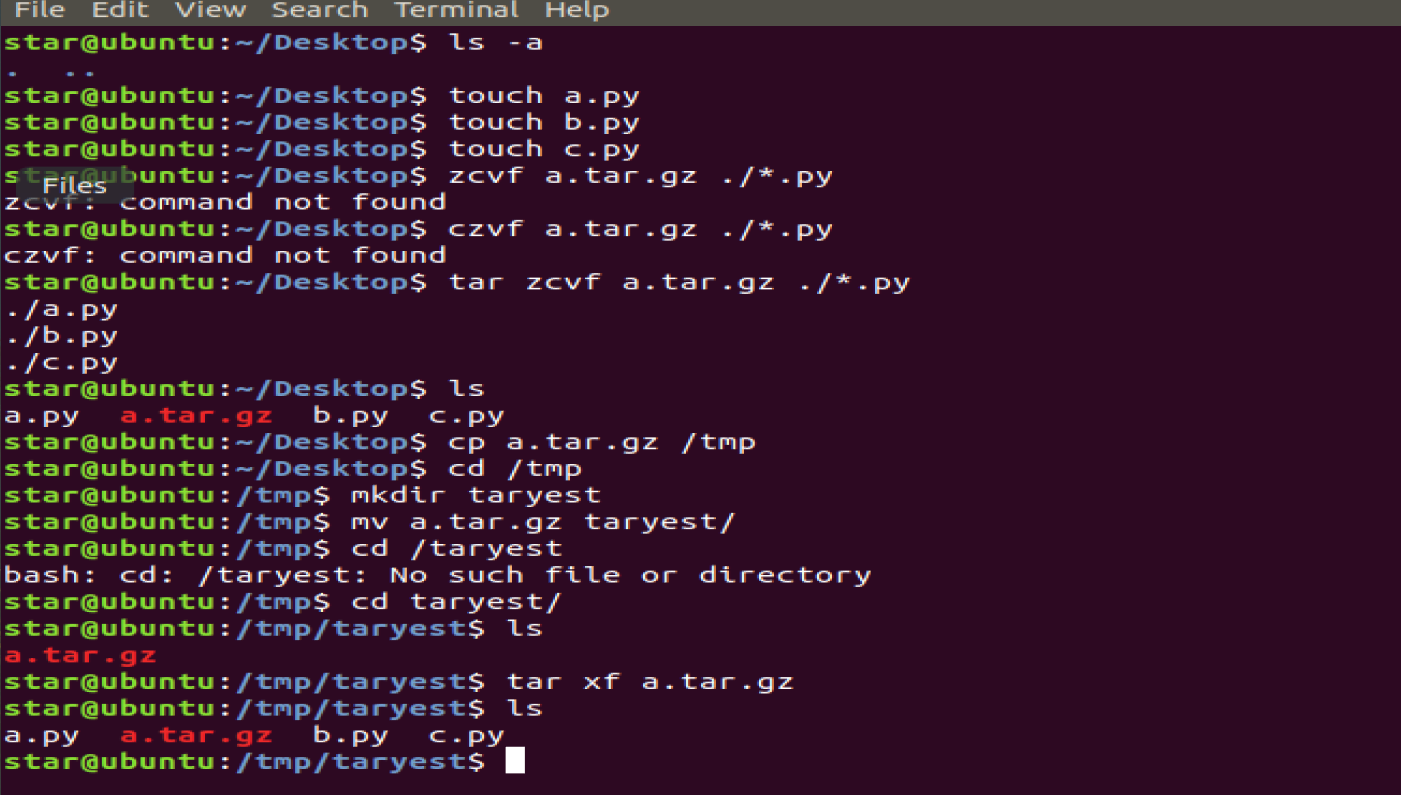
tar -xf  a.tar.gz   #
tar -xf  a.tar.gz  -C /tmp  # 指定解包路径
3.grep
找含有better的行,grep better a.txt
找不含有better的行,grep -v  better a.txt
grep -v  better a.txt列出在那个文件里面进行查找
只显示搜索的关键字： ,grep -o  better a.txt
不区分大小写：grep -i  better a.txt
显示搜索的关键字在哪一行： ,grep -on  better a.txt 或者grep -n  better a.txt

grep -E 与 egrep等价