CF399B Red and Blue Balls

题目

CF399B

洛谷RemoteJudge

思路

很容易发现,栈中靠上的蓝色球的出栈,对它下方的蓝色球没有影响.

举个例子:

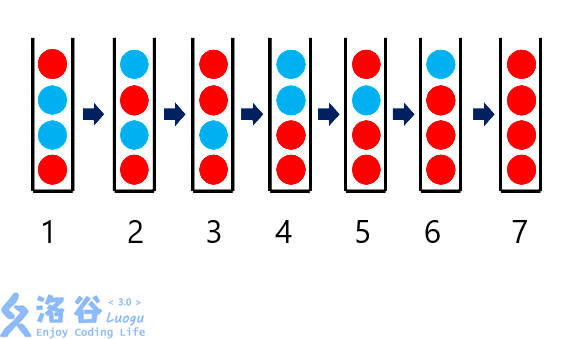
第一步中靠上的蓝色球在第三步出栈了,这一过程对它下面的蓝色球(即第一步中靠下的蓝色球)没有产生影响.

这启示我们由上到下分别计算每一颗(初始状态下的)蓝色球出栈需要的步数,再相加得到答案.

不妨设\(f(x)\)表示离栈顶距离为\(x\)的蓝色球出栈需要的步数,那么上面的样例的答案即为\(f(2)+f(3)\),即"离栈顶距离为\(2\)的蓝色球出栈所需步数\(+\)离栈顶距离为\(3\)的蓝色球出栈所需步数".

接下来的问题就是求\(f(x)\)函数的值.

显然\(f(1)=1\),即如果该球在栈顶,出栈需要\(1\)步操作.

考虑更一般的情况,我们会发现一个蓝色球想出栈的第一步,一定是将该蓝色球所在位置变为红色球,再将上方所有红色球变为蓝色球.

例如上面例子中的\("3\rightarrow4"\)这一步,原在从顶到下第三个位置的蓝色球想出栈,第一步就是把从顶到下第三个位置变为红色球,同时把从顶到下第一/二个位置变为蓝色球.

于是可以得到递推方程:

\[f(x)=f(1)+f(2)+...+f(x-1)+1\quad(x\geq2)
\]

也就是说,从顶到下第\(x\)个位置的蓝色球想出栈,等效于先走一步变为 "\(x\)位置红,\(1...x-1\)位置蓝",再让\(1...x-1\)位置的蓝色球依次出栈.

由于这道题数据范围较小,我们当然可以\(O(n^2)\)计算所有\(f(x)\)的值,但我们也可以推推通项公式.

由递推式,有

\[f(i-1)=f(1)+f(2)+...+f(i-2)+1
\]

所以

\[f(i)=f(1)+f(2)+...+f(i-2)+f(i-1)+1
\]

\[f(i)=[f(1)+f(2)+...+f(i-2)+1)]+f(i-1)
\]

\[f(i)=2\times f(i-1)
\]

所以

\[f(i)=2^{i-1}
\]

所以

\[ans= \sum_{if \space s[i]==B} (2^{i-1})
\]

实际代码中,需要注意字符串的下标从\(0\)开始.

代码

#include<bits/stdc++.h>
using namespace std;

int n;
long long ans,p;
string s;

int main()
{
	cin>>n>>s;
	for(int i=0;i<s.size();i++)
	{
		p= i==0? 1 : p*2;
		if(s[i]=='B')
			ans+=p;
	}
	cout<<ans;
	return 0;
}