【ZJOI2012】灾难 - LCA+拓扑排序

题目描述

阿米巴是小强的好朋友。

阿米巴和小强在草原上捉蚂蚱。小强突然想，如果蚂蚱被他们捉灭绝了，那么吃蚂蚱的小鸟就会饿死，而捕食小鸟的猛禽也会跟着灭绝，从而引发一系列的生态灾难。

学过生物的阿米巴告诉小强，草原是一个极其稳定的生态系统。如果蚂蚱灭绝了，小鸟照样可以吃别的虫子，所以一个物种的灭绝并不一定会引发重大的灾难。

我们现在从专业一点的角度来看这个问题。我们用一种叫做食物网的有向图来描述生物之间的关系：

一个食物网有N个点，代表N种生物，如果生物x可以吃生物y，那么从y向x连一个有向边。

这个图没有环。

图中有一些点没有连出边，这些点代表的生物都是生产者，可以通过光合作用来生存； 而有连出边的点代表的都是消费者，它们必须通过吃其他生物来生存。

如果某个消费者的所有食物都灭绝了，它会跟着灭绝。

我们定义一个生物在食物网中的“灾难值”为，如果它突然灭绝，那么会跟着一起灭绝的生物的种数。

举个例子：在一个草场上，生物之间的关系是：

如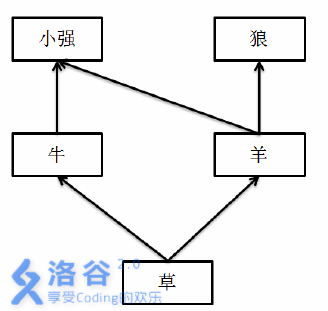 

如果小强和阿米巴把草原上所有的羊都给吓死了，那么狼会因为没有食物而灭绝，而小强和阿米巴可以通过吃牛、牛可以通过吃草来生存下去。所以，羊的灾难值是1。但是，如果草突然灭绝，那么整个草原上的5种生物都无法幸免，所以，草的灾难值是4。

给定一个食物网，你要求出每个生物的灾难值。

思路

一个生物灭绝仅当它的所有食物都灭绝了，而所有食物都灭绝仅当他们的LCA灭绝，因此我们把每个生物都连接在它的所有食物的LCA上，即每个节点的父节点是它的所有食物的LCA。按这样建树还有一个条件，就是这个生物加入之前它的所有食物都加入了，所以要按拓扑序加点，最后统计一下树上前缀和。

#include <bits/stdc++.h>
using namespace std;
const int maxn = 100000 + 10;
int n,deg[maxn],dep[maxn],father[maxn][25],size[maxn];
vector<int> edge1[maxn],edge2[maxn],tree[maxn];
queue<int> Q;
inline int lca(int a,int b) {
    if (dep[a] < dep[b]) swap(a,b);
    for (int i = 20;i >= 0;i--)
        if (dep[father[a][i]] >= dep[b]) a = father[a][i];
    if (a == b) return a;
    for (int i = 20;i >= 0;i--)
        if (father[a][i] != father[b][i]) {
            a = father[a][i];
            b = father[b][i];
        }
    return father[a][0];
}
inline void dfs(int now,int fa) {
    size[now] = 1;
    for (size_t i = 0;i < tree[now].size();i++)
        if (tree[now][i] != fa) {
            dfs(tree[now][i],now);
            size[now] += size[tree[now][i]];
        }
}
int main() {
    scanf("%d",&n);
    for (int i = 1,x;i <= n;i++)
        for (scanf("%d",&x);x;scanf("%d",&x)) {
            edge1[x].push_back(i);
            edge2[i].push_back(x);
            deg[i]++;

        }
    dep[n+1] = 1;
    for (int i = 1;i <= n;i++)
        if (!deg[i]) {
            Q.push(i);
            edge2[i].push_back(n+1);
        }
    while (Q.size()) {
        int now = Q.front(),LCA = edge2[now][0]; Q.pop();
        for (size_t i = 1;i < edge2[now].size();i++) LCA = lca(LCA,edge2[now][i]);
        dep[now] = dep[LCA]+1;
        father[now][0] = LCA;
        tree[LCA].push_back(now);
        for (int i = 1;i <= 20;i++) father[now][i] = father[father[now][i-1]][i-1];
        for (size_t i = 0;i < edge1[now].size();i++) {
            deg[edge1[now][i]]--;
            if (!deg[edge1[now][i]]) Q.push(edge1[now][i]);
        }
    }
    dfs(n+1,0);
    for (int i = 1;i <= n;i++) printf("%d\n",size[i]-1);
    return 0;
}