O2OA平台搭建

O2OA的开发环境非常简单，安装服务器后即可通过浏览器进行开发了和使用。具体可参考文档库中的其他文档，有比较详细的介绍，这里就不再赘述了。

Arduino开发发环境搭建

安装Arduino IDE

首先需要到Arduino官网下载并安装Arduino IDE。

下载地址：https://www.arduino.cc/en/software

安装好之后，我们就可以直接用Arduino IDE直接开发了，不过官方的IDE实在不怎么好用，做一些试验性的例子还行，想正真开发一个项目就有点力不从心了。以我个人的经验，使用VS Code的Arduino插件，以及基于Eclipse的sloeber都是不错的选择。

VS Code集成Arduino

下载和安装VS Code就不再细说了，安装完成后，进入“扩展”，搜索“Arduino”，安装“Arduino for Visual Studio Code”，Microsoft那个。

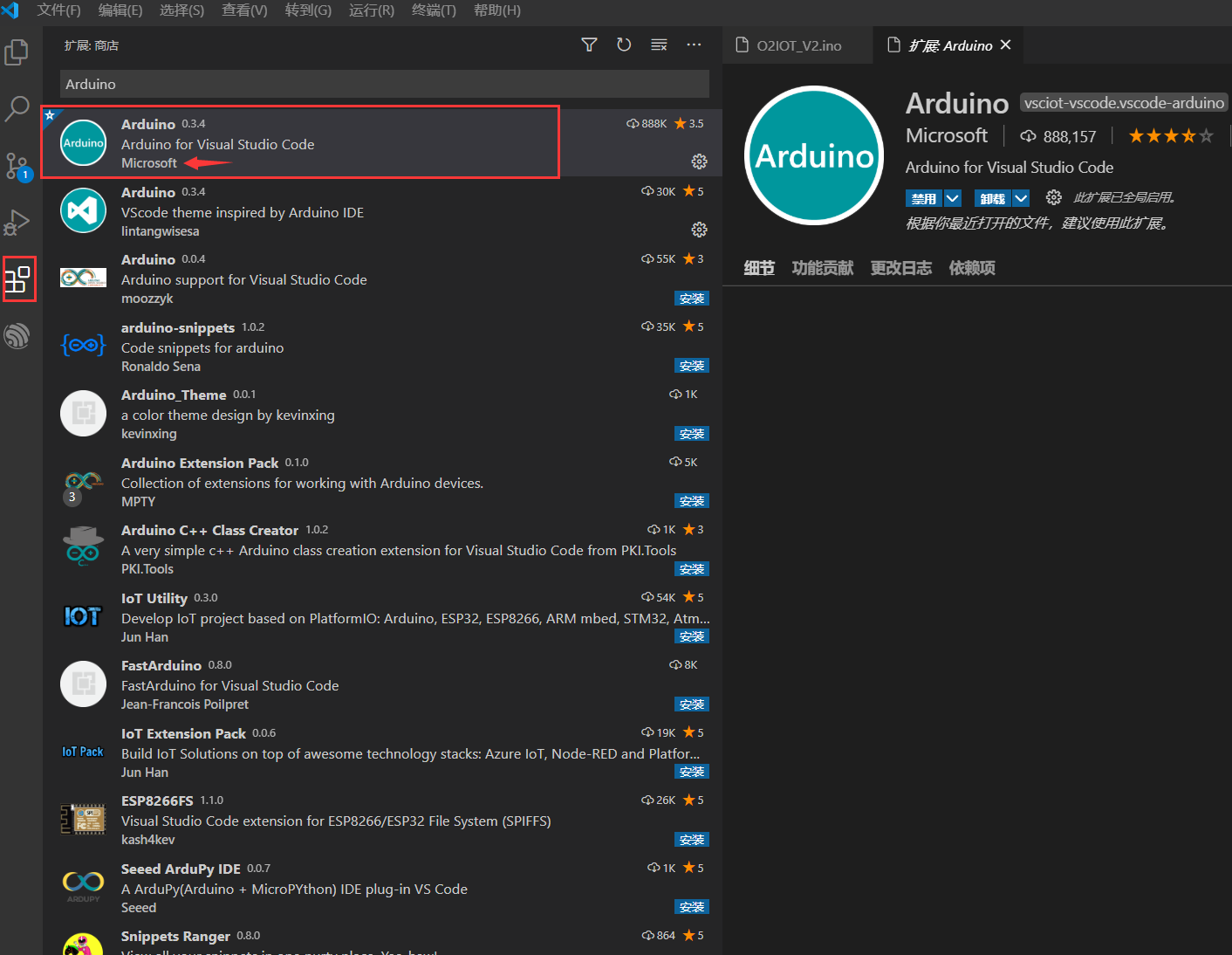
安装完成后，进入首选项设置（Ctrl+,）搜索“Arduino”，在“Arduino: Path”中输入你的Arduino IDE安装目录：

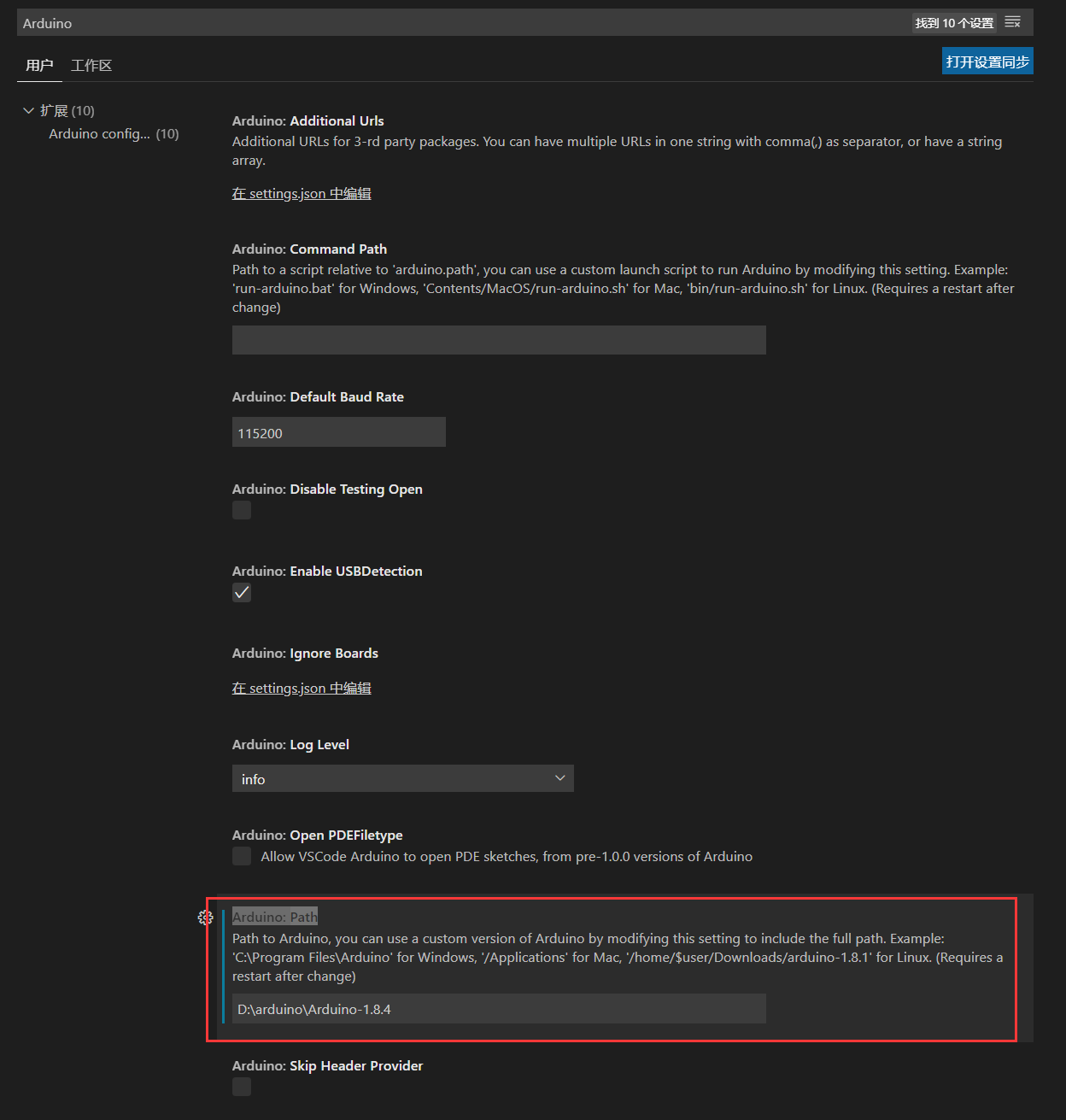
这样我们的VS Code就可以进行Arduino开发了。

安装开发板

我们使用ESP8266开发板进行开发，所以要安装ESP8266的开发板文件。

按F1，搜索“Arduino”，打开“Arduino: Board Manager”

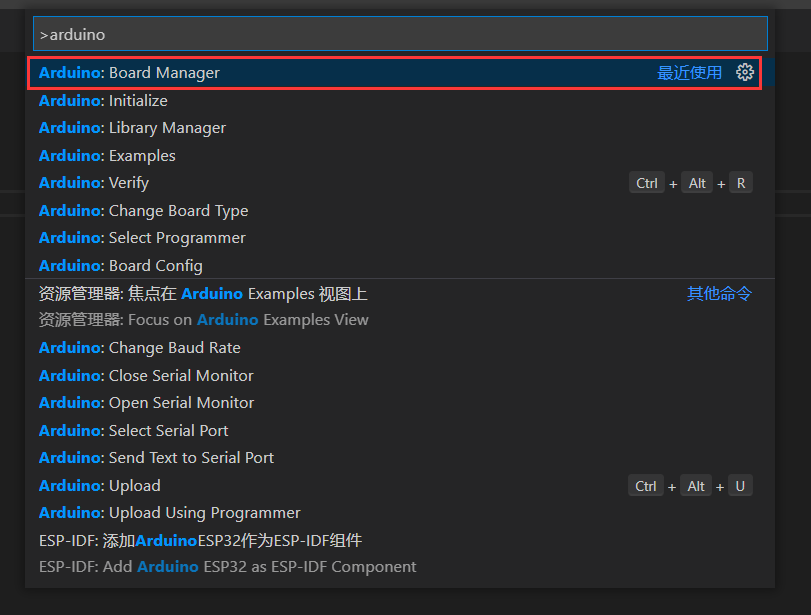
并搜索“ESP8266”，选择最新的版本，点击“install”。

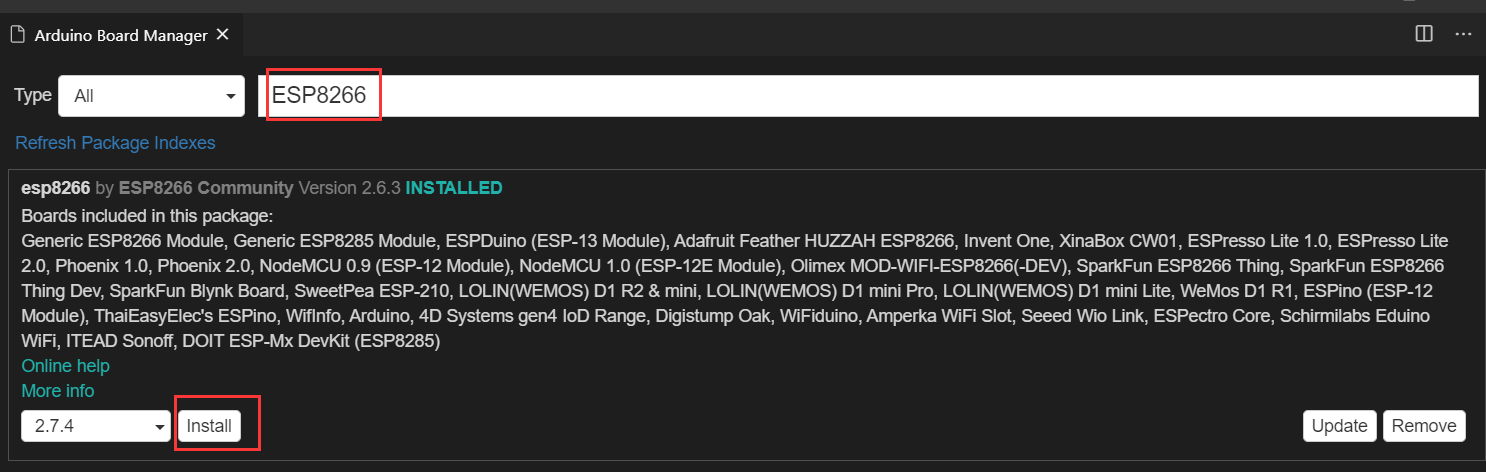
安装完成后就添加了对ESP8266芯片的各类开发板的支持了。

安装库文件

我们的项目中需要用到一些库，比如读取DHT22温度的库，WebSocket连接的库，Json解析库等，都需要事先安装。安装库也非常简单，按F1，搜索“Arduino”，打开“Arduino Library Manager”.

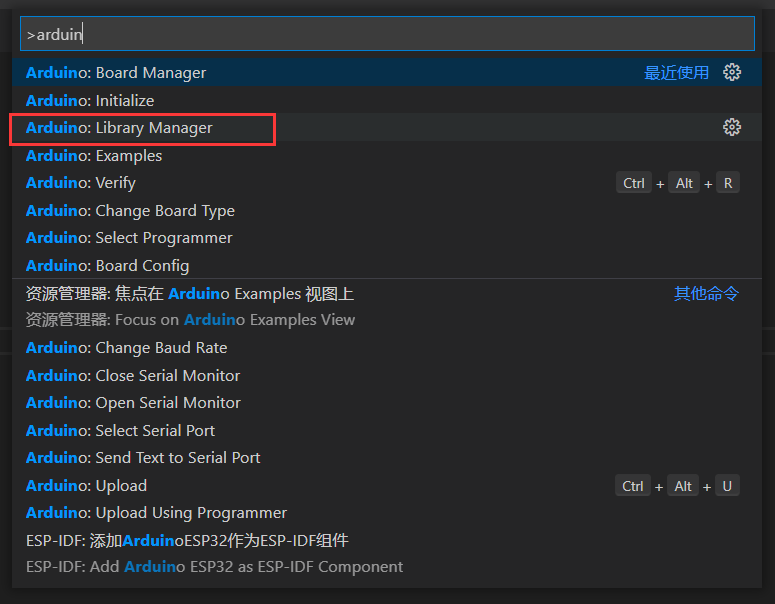
再搜索需要的库名称，如我们的项目中使用了ArduinoJson库来解析json，所以此处搜索“ArduinoJson”

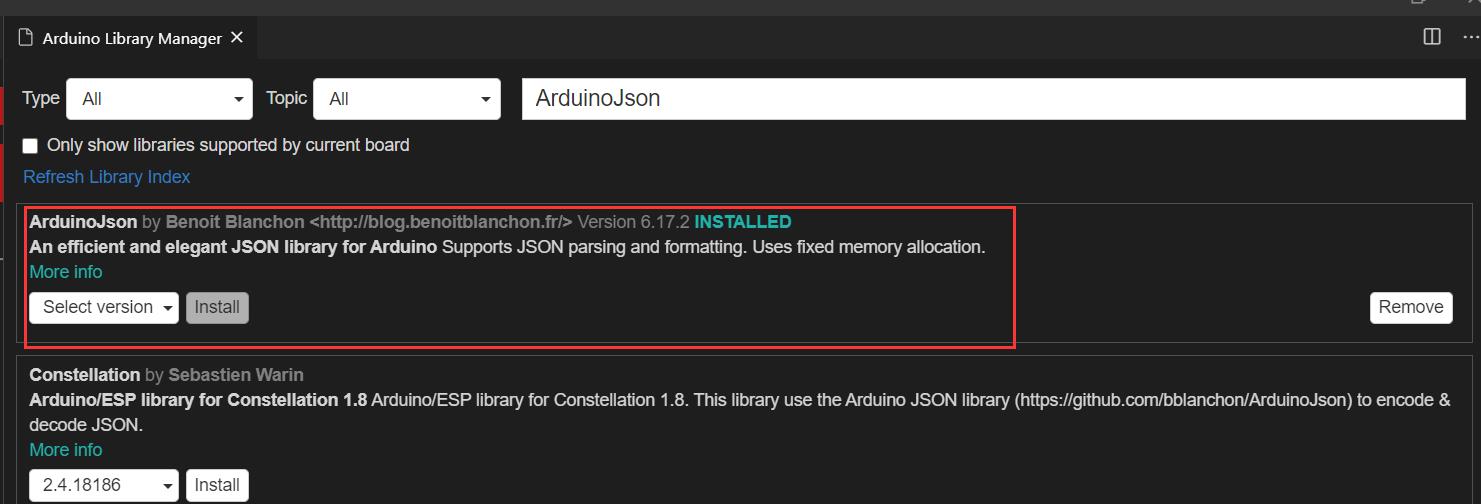
选择最新的版本，点击“install”即可。

安装了库后，一般都会有一些样例，我们可以在左下角的“ARDUINO EXAMPLES”中找到

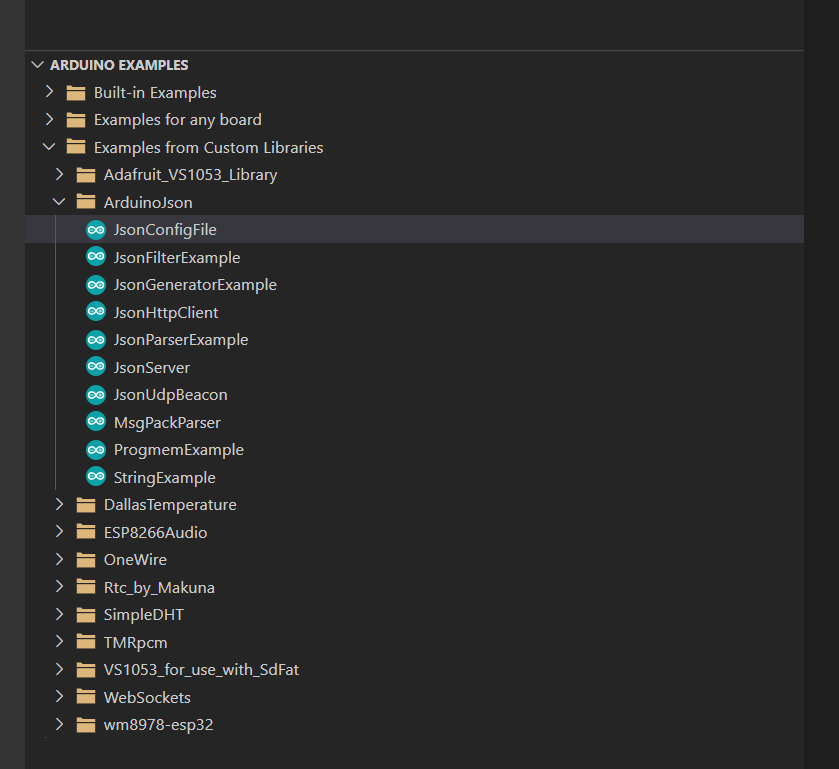
在我们这样项目中，需要安装的库如下：

  • ArduinoJson (An efficient and elegant JSON library for Arduino) by Benoit Blanchon
  • WebSockets (WebSockets for Arduino) by Markus Sattler
  • SimpleDHT (Arduino Temp & Humidity Sensors for DHT11 etc) by Winlin
  • DallasTemperature  (Arduino Library for Dallas Temperature ICs) by Miles Burton

安装驱动

此时，我们通过mirco usb线将ESP8266开发板连接到电脑，操作系统可能无法识别设备，需要安装USB转串口CH340驱动。大家自行根据不同操作系统搜索驱动程序，安装即可。

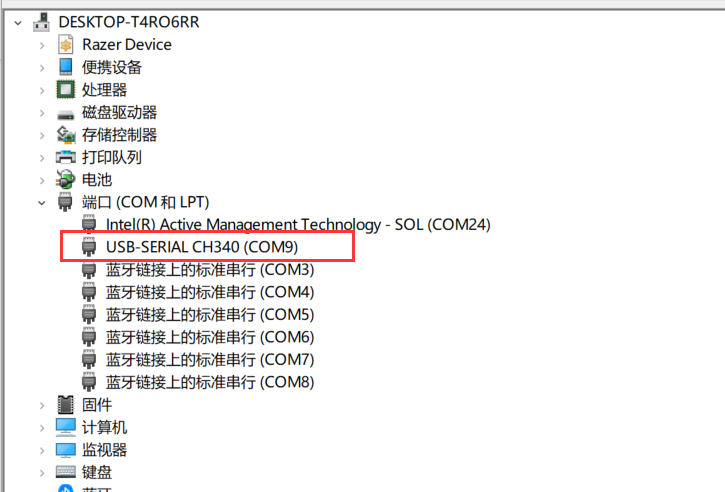
到此，我们的需要的开发环境都已经准备好了，下一步就可以进入实际的开发工作了。

开源OA办公平台搭建教程：O2OA+Arduino实现物联网应用（二）的更多相关文章

  1. 小白都会超详细--ELK日志管理平台搭建教程

    目录 一.介绍 二.安装JDK 三.安装Elasticsearch 四.安装Logstash 五.安装Kibana 六.Kibana简单使用 系统环境:CentOS Linux release 7.4 ...

  2. syslog-ng收集日志+ELK平台搭建教程

    syslog-ng部署: 用于接收交换机输出的日志. syslog-ng安装很简单,可以顺便搜一下,文章有很多.我是yum直接安装的. syslog-ng配置: vi /etc/syslog-ng/s ...

  3. 6 款国外开源web oa办公系统(转)

    国外的开源产品较多,而且大多提供免费的社区版本,oa办公系统也不例外. 1.eGroupware eGroupware是一个多用户,在以PHP为基础的API上的定制集为基础开发的,以WEB为基础的工作 ...

  4. oschina(开源中国)的Git代码托管平台使用教程

    oschina(开源中国)的Git代码托管平台使用教程 第一章 平台介绍 一. Git@OSC简介 开源中国的Git@OSC一个账号最多可以创建1000个项目,包含公有和私有,开源中国代码托管地址:h ...

  5. 【转】使用Apache Kylin搭建企业级开源大数据分析平台

    http://www.thebigdata.cn/JieJueFangAn/30143.html 本篇文章整理自史少锋4月23日在『1024大数据技术峰会』上的分享实录:使用Apache Kylin搭 ...

  6. 分布式任务调度平台XXL-JOB搭建教程

    关于分布式任务调度平台XXL-JOB,其实作者 许雪里 在其发布的中文教程中已经介绍的很清楚了,这里我就不做过多的介绍了,关于其搭建教程,本人依照其文档搭建起来基本上也没遇到啥问题,这里通过博客的形式 ...

  7. PaaS平台– Google App Engine的开源实现AppScale环境搭建

    搭建好开发环境介绍: 硬件平台:HP Z800 工作站  内存:24GB      硬盘:1TB 虚拟化环境:XenServer 6.2.0 VM1:Ubuntu 12.04 amd64 server ...

  8. 使用Apache Kylin搭建企业级开源大数据分析平台

    转:http://www.thebigdata.cn/JieJueFangAn/30143.html 我先做一个简单介绍我叫史少锋,我曾经在IBM.eBay做过大数据.云架构的开发,现在是Kylige ...

  9. Ubuntu Desktop基本办公环境搭建

    Ubuntu Desktop基本办公环境搭建 一如前面所强调的, linux系统是面向开发人员友好的,而对office办公人员并不友好 . 如果是重度的office办公需求人员,不建议使用linux ...

  10. dzzoffice协同办公平台与onlyoffice在线协作平台安装与部署

    1.安装dzzoffice协同办公平台 DzzOffice是一套开源办公套件,适用于企业.团队搭建自己的 类似“Google企业应用套件”.“微软Office365”的企业协同办公平台. 官网地址:h ...

随机推荐

  1. PHP while使用

    $i = 0; while(true){ if($i == 0){ $i++; continue; }else if($i > 10){ break; }else{ echo $i." ...

  2. javascript基础语法——词法结构

    × 目录 [1]java [2]定义 [3]大小写[4]保留字[5]注释[6]空白[7]分号 前面的话 javascript是一门简单的语言,也是一门复杂的语言.说它简单,是因为学会使用它只需片刻功夫 ...

  3. java servlet+mysql全过程(原创)

    前段时间写过一篇 servlet+oracle的文章,但是那是因为公司有可能接那么一个项目,然后我当时也比较闲,所以随便学了下,那玩意是白去研究了,因为公司后面并没接到那项目. 这次学servlet用 ...

  4. Python 字典(Dictionary)操作详解

    Python 字典(Dictionary)的详细操作方法. Python字典是另一种可变容器模型,且可存储任意类型对象,如字符串.数字.元组等其他容器模型. 一.创建字典 字典由键和对应值成对组成.字 ...

  5. R语言实战读书笔记2—创建数据集(上)

    第二章 创建数据集 2.1 数据集的概念 不同的行业对于数据集的行和列叫法不同.统计学家称它们为观测(observation)和变量(variable) ,数据库分析师则称其为记录(record)和字 ...

  6. 如何配置adb环境变量

    如何配置adb环境变量? 1.我的电脑---控制面板---高级系统设置 2.点击[高级系统设置],弹出系统属性的弹框, 3.点击[环境变量],弹出环境变量弹框,新建一个系统变量,命名为Android ...

  7. cp命令 复制目录

    格式:cp -R {源目录地址} {目标目录地址} 假设文件夹download下有两个目录 download/a download/b 现在想将文件夹a复制到文件夹b下,执行 cp -R downlo ...

  8. mysql 必须掌握的工具pt-query-digest安装

    mysql 必须掌握的工具pt-query-digest 古人云:工欲善其事,必先利其器.作为一名优秀的mysql dba也需要有掌握几个好用的mysql管理工具,所以我也一直在整理和查找一些能够便于 ...

  9. 深入学习AngularJS中数据的双向绑定机制

    来自:http://www.jb51.net/article/80454.htm Angular JS (Angular.JS) 是一组用来开发Web页面的框架.模板以及数据绑定和丰富UI组件.它支持 ...

  10. 当您在 64 位 Windows 上运行 Regsvr32.exe 时出现错误信息

    尝试运行 Regsvr32.exe 注册在 64 位版本的 Windows 32 位动态链接库 (DLL) 时您会收到以下错误消息: 若要解决此问题,从 %SystemRoot%\Syswow64 文 ...