三维网格补洞算法（Radial Basis Function）

　　在逆向工程中，由于设备或模型的原因，我们获取得到的三维模型数据往往并不完整，从而使得生成的网格模型存在孔洞，这对后续的模型分析会造成影响。下面介绍一种基于径向基函数（RBF：Radial Basis Function）的三角网格补洞方法。

Step 1：检测孔洞边界

　　三角网格是由一系列顶点（V）以及由这些顶点所构成的三角面片（F）所组成，由三角面片可以得到网格的边（E）。通常一条边连接两个三角面片，这种边称为网格内部边，而如果某条边仅连接一个三角面片，那么称这条边为网格边界边，所有的边界边按顺序连接之后就形成了网格的孔洞。

Step 2：初始化网格

　　为了使孔洞填充简单、健壮，可以采用最小角度法进行网格修补，具体步骤如下：

　　（1）得到孔洞边界点信息，计算边界边长度的平均值l。

　　（2）计算每个边界点的两条相邻边的夹角大小。

　　（3）找出具有最小夹角的边界点，计算它的两个相邻边界点的距离s，判断s < 2×l是否成立：若成立，则按下图所示增加一个三角形，若不成立则增加两个三角形。

　　（4）更新边界点信息。

　　（5）判断孔洞是否修补完整，若未完整，转（2），否则结束。

Step 3：最小二乘网格

　　初始化补洞得到的网格质量不是很好，我们需要优化网格顶点的位置，优化的条件是：

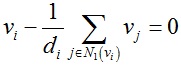
其中d_i为顶点v_i的1环邻域顶点数。

　　上式可以用一个线性方程组来描述：LV = 0，其中L是Laplace矩阵，具体形式为，矩阵L的秩等于n – k，n为网格顶点的数目，k为网格连通区域的个数，如果网格是全连通的，那么矩阵L的秩是n – 1。因此如果我们要使方程有解，需要加入m（m ≥ k）个控制顶点坐标v_s作为方程的边界条件，在实际中我们将初始化网格的边界顶点作为控制顶点。

　　其实上述线性方程组的求解等价于如下能量函数最小化的求解：

　　能量函数的第一部分是使得网格顶点尽量光滑，即每个顶点位于其1环邻域顶点的中心，第二部分是为了控制顶点的位置满足要求。

　　最小二乘网格的优势是能够生成高质量的光滑网格，生成过程仅需要网格的拓扑连接关系和少数控制点的坐标信息。

Step 4：径向基函数（RBF）隐式曲面

　　径向基函数是一个仅依赖于离控制点c距离的函数，即h(x,c) = h(||x - c||)，距离通常是欧式距离，也可以是其他形式距离。径向基函数网络是一个三层BP网络，其可以表示为多个基函数的线性组合：

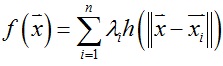
　　下面列出2个最常用的基函数形式：

　　（1）Gaussian：h(r) = e^-(εr)2

　　（2）Polyharmonic spline：h(r) = r^k，k = 1、3、5、… 或h(r) = r^kln(r)，k = 2、4、6、…

　　利用径向基函数网络并通过给定控制点x_i和对应的值f_i之后，可以求解得到网络中的系数λ_i，因此径向基函数网络能够解决空间散乱数据点的平滑插值问题，函数的零等值面就是我们要求的曲面。

　　在实际求解时函数f(x)表达式中通常会增加一个一次多项式P(x)，如下：

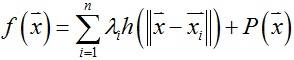，其中：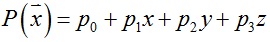

　　将控制点位置x_i和值f_i代入函数f(x)可以得到如下方程，求解之后即可确定隐式曲面f(x)。

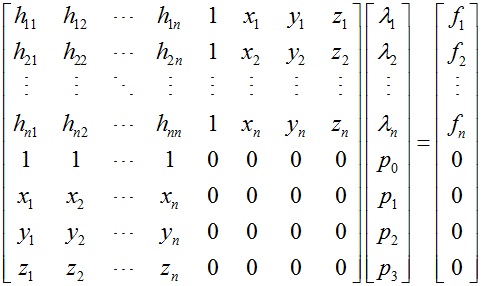
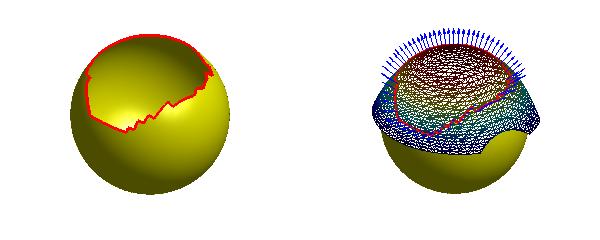
　　控制点x_i可分为三类：

　　（1）边界控制点：曲面通过的点，f(x_i) = 0

　　（2）外部控制点：将边界控制点沿法向正方向移动一小段距离而得到的控制点，取f(x_i) = -1

　　（3）内部控制点：将边界控制点沿法向负方向移动一小段距离而得到的控制点，取f(x_i) = 1

　　计算时我们选择的基函数为h(r) = r³，其实此时隐式曲面函数满足Δ³f = 0，将基函数代入后得到隐式曲面的表达式如下：

function options = RBF_Create(x, y, type)
    % x: input data; y: input data value
    options = [];
    options.nodes = x;
    switch type
        case 'linear'
            options.phi = @rbfphi_linear;
        case 'cubic'
            options.phi = @rbfphi_cubic;
    end    

    [n, dim] = size(x);
    A = zeros(n,n);
    for i = :n
        r = normrow(bsxfun(@minus, x(i,:), x));
        temp = feval(options.phi, r);
        A(i,:) = temp';
        A(:,i) = temp;
    end
    % Polynomial part
    P = [ones(n,) x];
    A = [ A      P
          P' zeros(dim+1, dim+1)];
    B = [y; zeros(dim+, )];

    coeff = A\B;
    options.coeff = coeff;
end

% Radial Base Functions
function u = rbfphi_linear(r)
    u = r;
end
function u = rbfphi_cubic(r)
    u = r.*r.*r;
end

Step 5：牛顿插值

　　为了得到插值隐式曲面的网格，我们需要把最小二乘网格的顶点投射到隐式曲面上，这里我们采用牛顿迭代法：

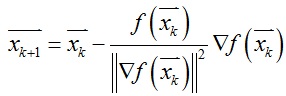
　　最小二乘网格的顶点位置作为迭代初始条件，当||x_k+1 – x_k|| < ε时，迭代停止，ε为设定的误差。上式中梯度表达式如下：

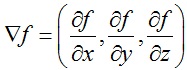
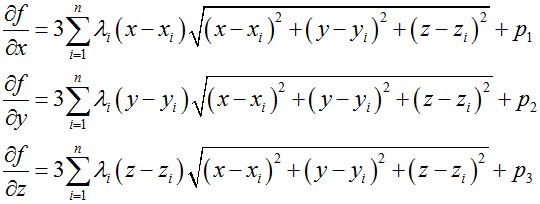
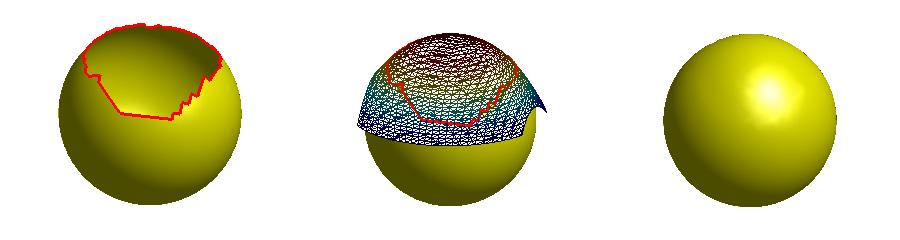
效果：

本文为原创，转载请注明出处：http://www.cnblogs.com/shushen

参考文献：

[1] Olga Sorkine and Daniel Cohen-Or. 2004. Least-Squares Meshes. In Proceedings of the Shape Modeling International 2004 (SMI '04). IEEE Computer Society, Washington, DC, USA, 191-199.

[2] Greg Turk and James F. O'Brien. 1999. Shape transformation using variational implicit functions. In Proceedings of the 26th annual conference on Computer graphics and interactive techniques (SIGGRAPH '99). ACM Press/Addison-Wesley Publishing Co., New York, NY, USA, 335-342.

[3] 袁天然. 三角网格模型光顺简化和缝补技术的研究及应用[D]. 南京航空航天大学, 2007.