实用教程！SPSSAU验证性因子分析思路总结

验证性因子分析，是用于测量因子与测量项(量表题项)之间的对应关系是否与研究者预测保持一致的一种研究方法。尽管因子分析适合任何学科使用，但以社会科学居多。

目前有很多软件都可以非常便利地实现验证性因子分析，本文将基于SPSSAU系统进行说明。

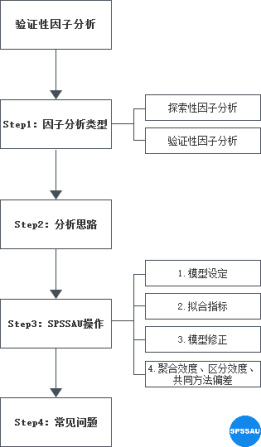
验证性因子分析

Step1：因子分析类型

因子分析可分为两种类型：探索性因子分析（EFA）和验证性因子分析（CFA）。

探索性因子分析，主要用于浓缩测量项，将所有题项浓缩提取成几个概括性因子，达到减少分析次数，减少重复信息的目的。

验证性因子分析与探索性因子分析相似，两者区别只在于探索性因子分析(EFA)用于探索因子与测量项之间的对应关系，验证性因子分析(CFA)用于验证结果与理论预期是否一致。

Step2：分析思路

 

在实际研究中，验证性因子分析常会与结构方程模型、路径分析等方法联系到一起，对于不熟悉概念的研究人员容易搞混这些方法，下表对这几种方法进行简单说明：

 

方法	功能	其它说明
探索性因子分析（EFA）	研究测量关系	适用于非经典量表
验证性因子分析（CFA）	研究测量关系	适用于经典量表
回归分析	研究自变量对一个因变量的影响关系	y为定量数据
路径分析	研究多个自变量与多个因变量之间的影响关系	可先用CFA/EFA确定因子与研究项关系，再进行路径分析
结构方程模型	研究影响关系及测量关系	结构方程模型包括两部分： 验证性因子分析和路径分析

探索性因子分析：验证因子与分析项的对应关系，检验量表效度，非经典量表通常用探索性因子分析。

验证性因子分析：验证因子与分析项的对应关系，检验量表效度，成熟量表通常用验证性因子分析。确认测量关系后，后续可进行路径分析/线性回归分析研究具体的影响关系。

路径分析：用于研究多个自变量与多个因变量影响关系；如果因变量只有一个，可以使用线性回归分析。

结构方程模型SEM：包括测量关系和影响关系。如果仅包括影响关系，此时称作路径分析（Path analysis，有时也称通径分析）。通常需要进行探索性因子分析和验证性因子分析，均保证测量关系无误之后，再进行结构方程模型构建。

从分析思路上看，建议先用探索性因子分析EFA构建模型，确定存在几个因子及各分析项与因子的对应关系，再用验证性因子分析CFA加以检验。

 

Step3：SPSSAU操作

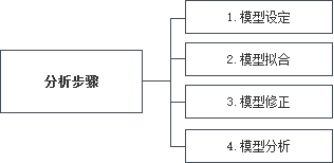
分析步骤

（1）模型设定

 

首先需要确定因子数及对应分析题项，顺序放入分析框内。

 

 

 

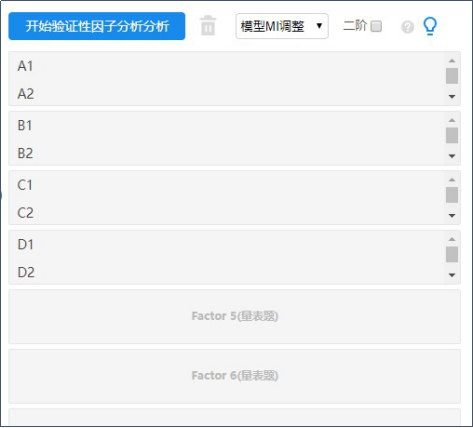
模型MI调整：用于修正模型拟合度，一般在模型拟合情况不佳时使用。通常情况下不需要设置。

二阶：验证性因子分析包括一阶和二阶，绝大多数情况下均为一阶验证性因子分析。如果说验证性因子分析时为二阶模型，可以勾选‘二阶’项即可。

（2）模型拟合

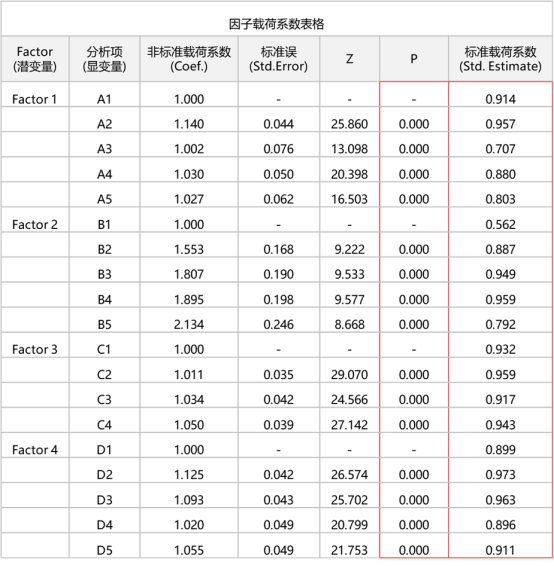
因子载荷系数表格

通过因子载荷系数表格可以展示因子(潜变量)与分析项(显变量)之间的关系情况。如果因子与测量项间的对应关系出现严重偏差，或者因子载荷系数值过低，则需要删除掉该测量项。

分析时主要关注P值及标准载荷系数，建议结合SPSSAU给出的“分析建议”进行分析。

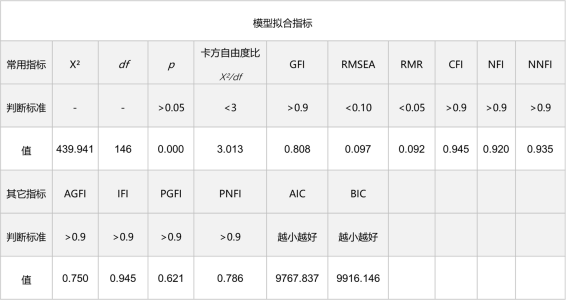
模型拟合指标

模型拟合指标用于整体模型拟合效度情况分析。

常用的拟合值及其判断标准，都展示在上表中，实际输出值在标准范围内及说明模型拟合程度较好。模型拟合指标非常多,通常下很难保证所有指标均达标，只要多数指标达标或接近标准值即可。

*常用指标包括卡方自由度比，GFI，RMSEA，RMR，CFI，NFI和NNFI。

（3）模型修正

根据模型拟合指标情况，评价模型的优劣，如果模型拟合情况不佳，则需要进一步修正模型。

MI指标越大说明该项与其他因子的相关性越强，MI过大时会干扰模型需要进行修正或剔除该项。

模型构建过程需要重复多次，以找到最优模型。同时SPSSAU会自动生成模型结果图。

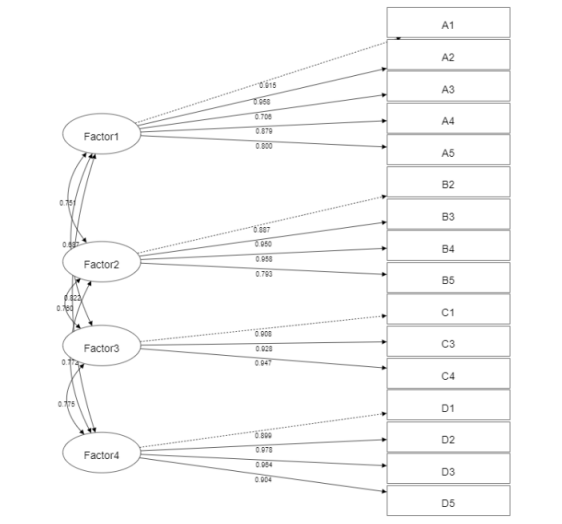
（4）模型分析

在完成模型构建后，即可使用模型进行分析。验证性因子分析主要有三个方面的功能，分别是聚合效度、区分效度、共同方法偏差。

聚合效度

聚合效度，也叫做收敛效度。AVE和CR是用于判断聚合效度的常用指标，AVE>0.5，并且CR>0.7，则说明具有良好的聚合效度。如果AVE或CR值较低,可考虑移除某因子后重新分析聚合效度。

上图为SPSSAU输出的AVE、CR值指标表格，可以根据此表格进行查看。

区分效度

区分效度，常用的做法是将AVE根号值与‘相关系数值’进行对比，SPSSAU也会输出相应结果。

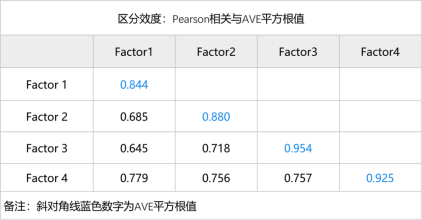
如果每个因子的AVE根号值均大于“该因子与其它因子的相关系数最大值”，说明具有良好的区分效度。

共同方法偏差

共同方法偏差，SPSSAU提供两种方法检验，一种是探索性因子分析(也称作Harman单因子检验方法)，做法是将所有变量进行探索性因子分析，如果只得出一个因子或者第一个因子的解释力（方差解释率）特别大，则判定存在共同方法偏差。

另一种是验证性因子分析，所有变量全部放在一个因子里面进行分析，如果测量出来显示模型的拟合指标无法达标，模型拟合不佳，说明所有的测量项并不应该同属于一个因子，也就说明数据无共同方法偏差问题。

Step4：常见问题

 

l 验证性因子分析需要较大的样本量，通常建议样本量至少为测量项(量表题)的5倍以上，最好10倍以上，且一般情况下至少需要200个样本。

l 一个因子对应的测量项最好在5~8个之间，便于后续删除掉不合理测量项。

l 绝大多数情况下均为一阶验证性因子分析。如果说验证性因子分析时为二阶模型，此时参数处选中‘二阶’即可。

总结：

一般来说，使用验证性因子分析需要有一定的理论基础支持，如果拟合指标不能达标，最好按照分析思路：探索性因子分析→验证性因子分析，进行分析。

以及对于不熟悉的步骤，建议大家阅读SPSSAU帮助手册中的相关说明以及SPSSAU的教学视频。