通俗易懂的 Java 位操作运算讲解

所有数值都是2进制

软件开发者都知道 10 进制、16 进制、8 进制。 
比如数字 10 的各位进制形式表现如下。

十进制：10
八进制：012
十六进制：0x0a
二进制：1010

原码 反码 补码

我们已经知道了一个 int 型数值是 4 个字节。每个字节有 8 位。但对于一个 int 或者其它整数类型如 （long）的数值而言还要注意的是，它的最高位是符号位。

• 最高位为0表示正数。
• 最高位为1表示负数

原码 将一个数字转换成二进制就是这个数值的原码。

int a = 5; //原码  0000 0000 0000 0101
int b = -3;  //原码  1000 0000 0000 0011

反码 
分两种情况：正数和负数

• 正数 正数的反码就是原码。
• 负数 负数的反码是在原码的基础上，符号位不变 其它位都取反。

5 的原码：0000 0000 0000 0101

-3 的原码：1000 0000 0000 0011
-3 的反码：1111 1111 1111 1100

补码 
仍然分正数和负数两种情况

• 正数 正数的补码就是原码。
• 负数 负数的补码在反码的基础上加1。

5 的补码：0000 0000 0000 0101

-3 的反码：1111 1111 1111 1100
-3 的补码: 1111 1111 1111 1101

计算机在进行数值运算的时候，是通过补码表示每个数值的。

比如

5 - 3 = 5 + ( -3 )
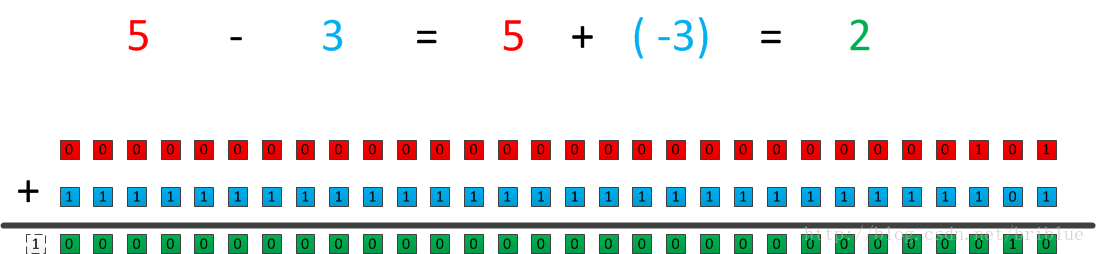
相当于 0000 0000 0000 0101 + 1111 1111 1111 1101
    = 1 0000 0000 0000 0010

最后的结果是1 0000 0000 0000 0010 这样的二进制，由于 int 类型只有 4 byte，所以最高位产生了溢出，进位 1 被丢弃。结果就变成了 0010 也就是 2，5 - 3 = 2 没有毛病。

位运算符 &、|、~、^、>>、<<

位运算符包含与运算符、或运算符、取反运算符、异或运算符、左移运算符和右移运算符。在下面的内容中，我将会一一讲解。

需要注意的是，下面测试用的数据都是 int 类型，int 类型是 4 个字节长度，但是为了方便说明示例中用的数值我都用 1 个字节表示。希望不会给大家造成困扰。

& 与运算符

规则 与运算时，进行运算的两个数，从最低位到最高位，一一对应。如果某 bit 的两个数值对应的值都是 1，则结果值相应的 bit 就是 1，否则为 0.

0 & 0 = 0,

0 & 1 = 0,

1 & 1 = 1

3 & 5 = 1 这是因为

0000 0011

&

0000 0101

=

0000 0001

按照规则，将两个数值按照低位到高位一一对齐运算，因为只有第 0 位都为 1，所以计算结果为 1.

| 或运算符

规则 与运算时，进行运算的两个数，从最低位到最高位，一一对应。如果某 bit 的两个数值对应的值只要 1 个为 1，则结果值相应的 bit 就是 1，否则为 0。

0 | 0 = 0,

0 | 1 = 1,

1 | 1 = 1

3 | 5 = 7 这是因为

0000 0011

|

0000 0101

=

0000 0111

~ 取反运算符

规则 对操作数的每一位进行操作，1 变成 0，0 变成 1。

~5 =>  0000 0101   ~  => 1111 1010

^ 异或运算符

规则 两个操作数进行异或时，对于同一位上，如果数值相同则为 0，数值不同则为 1。

1 ^ 0 = 1,

1 ^ 1 = 0,

0 ^ 0 = 0;

3 ^ 5 = 6,这是因为

0000 0011

|

0000 0101

=

0000 0110

值得注意的是 3 ^ 5 = 6,而 6 ^ 5 = 3

0000 0110

|

0000 0101

=

0000 0011

针对这个特性，我们可以将异或运算作为一个简单的数据加密的形式。比如，将一个mp4文件所有数值与一个种子数值进行异或得到加密后的数据，解密的时候再将数据与种子数值进行异或一次就可以了。

所以说异或运算可以作为简单的加解密运算算法。

>> 右移运算符

规则 a >> b 将数值 a 的二进制数值从 0 位算起到第 b - 1 位，整体向右方向移动 b 位，符号位不变，高位空出来的位补数值 0。

5 >> 1 ===>  1000 0000 0000 0101 >> 1  = 1000 0000 0000 0010 = 2
7 >> 2 ===>  1000 0000 0000 0111 >> 2  = 1000 0000 0000 0001 = 1
9 >> 3 ===>  1000 0000 0000 1001 >> 3  = 1000 0000 0000 0001 = 1
11 >> 2 ===> 1000 0000 0000 1011 >> 2 = 1000 0000 0000 0010 = 2

大家发现什么规律没有？a >> b = a / ( 2 ^ b ) ,所以 5 >> 1= 5 / 2 = 2,11 >> 2 = 11 / 4 = 2。

<< 左移运算符

规则 a << b 将数值 a 的二进制数值从 0 位算起到第 b - 1 位，整体向左方向移动 b 位，符号位不变，低位空出来的位补数值 0。

5 << 1 ===>  1000 0000 0000 0101 << 1  = 1000 0000 0000 1010 = 10
7 << 2 ===>  1000 0000 0000 0111 << 2  = 1000 0000 0001 1100 = 28
9 << 3 ===>  1000 0000 0000 1001 << 3  = 1000 0000 0100 1000 = 72
11 << 2 ===> 1000 0000 0000 1011 << 2 = 1000 0000 0010 1100 = 44

很明显就可以看出 a << b = a * (2 ^ b)

综合上面两个可以看到，如果某个数值右移 n 位，就相当于拿这个数值去除以 2 的 n 次幂。如果某个数值左移 n 位，就相当于这个数值乘以 2 ^ n。