hdu-2620 Ice Rain---数论（取模运算规律）

题目链接：

http://acm.hdu.edu.cn/showproblem.php?pid=2620

题目大意：

给出n和k求：

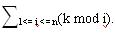
解题思路：

kmodi=k-i*[k/i] ，所以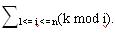=nk-（1*[k/1]+2*[k/2]+...+n*[k/n]）

只需求（1*[k/1]+2*[k/2]+...+n*[k/n]）

对于前sqrt(k)项，可以直接求解

对于后面的，可以枚举[k/i]取整得到的值来计算有多少个这样的值。

这样时间复杂度只有根号k

比如k = n = 25，需要求解（1*[k/1]+2*[k/2]+...+n*[k/n]）

对于前5项，直接求解

6到25项的结果分别是：

i	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25
[k/i]	4	3	3	2	2	2	2	1	1	1	1	1	1	1	1	1	1	1	1	1

从6开始

[k/i] = 4 左区间：6　　右区间为25 / 4 = 6

[k/i] = 3 左区间：7　　右区间为25 / 3 = 8

[k/i] = 2 左区间：9　　右区间为25 / 2 = 12

[k/i] = 1 左区间：13　  右区间为25 / 1 = 25

可写出伪代码：

　　i从sqrt(k)+1到k

　　　　左区间 l = i；

　　　　取整的值x为 k / l

　　　　右区间为 r = k / x

　　　　右区间取n和右区间的较小值

　　　　取整的值x的个数：num = (r - l + 1) * (r + l) / 2　　　　这是由于求的是（1*[k/1]+2*[k/2]+...+n*[k/n]）前面还有系数需要相加

　　　　tot += num * x

　　　　i = r + 1

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 int main()
 {
     ll n, k;
     while(cin >> n >> k)
     {
         ll a = n * k;
         if(n > k)n = k;
         ll m = sqrt(k + 0.5);
         ll tot = ;
         if(n > m)
         {
             for(ll i = ; i <= m; i++)
                 tot += k / i * i;
             for(ll i = m + ; i <= n; )//i就是左区间
             {
                 ll x = k / i;
                 ll r = k / x;           //r是右区间
                 if(r > n)r = n;
                 tot += (r + i) * (r - i + ) /  * x;
                 i = r + ;
             }
         }
         else
         {
             for(ll i = ; i <= n; i++)
                 tot += k / i * i;
         }
         ll ans = a - tot;
         cout<<ans<<endl;
     }
     return ;
 }