JZOJ.5236【NOIP2017模拟8.7】利普希茨
Description
Input
第一行一个整数n。
接下来一行n个整数,描述序列A。
第三行一个数q 。
接下来q行,每行三个整数。其中第一个整数type表示操作的类型。 type=0对应修改操作, type=1对应查询操作。
Output
对于每个查询,给出f(A[l..r]) 。
Sample Input
输入1:
6
90 50 78 0 96 20
6
0 1 35
1 1 4
0 1 67
0 4 11
0 3 96
1 3 5 输入2:
50
544 944 200 704 400 150 8 964 666 596 850 608 452 103 988 760 370 723 350 862 856 0 724 544 668 891 575 448 16 613 952 745 990 459 740 960 752 194 335 575 525 12 618 80 618 224 240 600 562 283
10
1 6 6
1 1 3
0 11 78279
0 33 42738
0 45 67270
1 1 26
1 19 24
1 37 39
1 8 13
0 7 64428
Sample Output
输出1:
78
85 输出2:
0
744
77683
856
558
77683
Data Constraint
对于60%的数据,n,q<=5000
对于100%的数据,n,q<=100000,0<=ai,val<=10^9
这里有一个结论:f(A)的最大值是相邻的两点的差值。
我们可以设想一下,一个区间被里面min和max分成了三段,其中i=min,j=max,那么设对应的f(A)的值为a,
那么我们可以枚举里面的左端点i右端点j来计算f(A)的值与a比较
首先很肯定的一点 区间[i,j]不能跨过min和max,那么我们会对这三段区间不断细分,到最后也就只剩下相邻的两个点了,此时就是最大值和最小值(这个似乎不能证明)
还有个几何证明:f(A)可以看成一个斜率的绝对值,那么对于坐标上的三个点a,b,c来说,它们三点确定的直线中,很显然横坐标越靠近的两个点斜率会越大
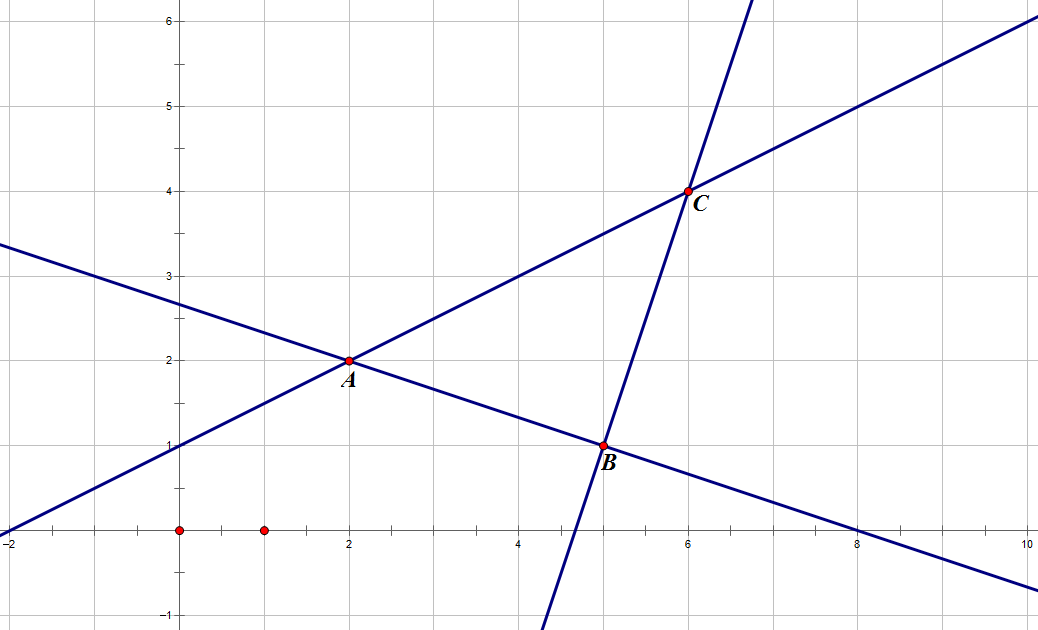
(转自mcw的证明)令$\Delta_i=A_{i+1}-A_i$,则$\left\lceil\frac{|A_j-A_i|}{j-i}\right\rceil=\left\lceil\frac{|\sum_{k=i}^{j-1}\Delta_k|}{j-i}\right\rceil=\overline{\Delta_{i\,..\,j-1}}$,显然会有$\Delta_i\,..\,\Delta_{j-1}$中的一项大于等于$\overline{\Delta_{i\,..\,j-1}}$
所以这题就变成了维护差值的修改和最值了,线段树就可以了。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<cmath>
using namespace std;
int maxx[],n,q,a[],x,l,r,d[];
void buildtree(int root,int l,int r){
if (l==r) {maxx[root]=d[l]; return;}
int mid=(l+r)>>;
buildtree(root<<,l,mid);
buildtree(root<<|,mid+,r);
maxx[root]=max(abs(maxx[root<<]),abs(maxx[root<<|]));
}
void change(int root,int l,int r,int x,int c){
if (l==r){
maxx[root]+=c;
return;
}
int mid=(l+r)>>;
if (x<=mid) change(root<<,l,mid,x,c);
if (x>mid) change(root<<|,mid+,r,x,c);
maxx[root]=max(abs(maxx[root<<]),abs(maxx[root<<|]));
}
int get(int root,int l,int r,int x,int y){
if ((x<=l)&&(y>=r)) return abs(maxx[root]);
int ans=;
int mid=(l+r)>>;
if (x<=mid) ans=max(ans,get(root<<,l,mid,x,y));
if (y>mid) ans=max(ans,get(root<<|,mid+,r,x,y));
return ans;
}
int main(){
freopen("lipschitz.in","r",stdin);
freopen("lipschitz.out","w",stdout);
scanf("%d",&n);
for (int i=;i<=n;i++){
scanf("%d",&a[i]);
d[i]=a[i]-a[i-];
}
buildtree(,,n);
scanf("%d",&q);
while (q--){
scanf("%d%d%d",&x,&l,&r);
if (x==) {change(,,n,l,r-a[l]);change(,,n,l+,-r+a[l]); a[l]=r;}
if (x==) printf("%d\n",get(,,n,l+,r));
}
return ;
}
神奇的代码
数学很重要
JZOJ.5236【NOIP2017模拟8.7】利普希茨的更多相关文章
- JZOJ 5236. 【NOIP2017模拟8.7A组】利普希茨
5236. [NOIP2017模拟8.7A组]利普希茨 (File IO): input:lipschitz.in output:lipschitz.out Time Limits: 1000 ms ...
- [jzoj 5343] [NOIP2017模拟9.3A组] 健美猫 解题报告 (差分)
题目链接: http://172.16.0.132/senior/#main/show/5343 题目: 题解: 记旋转i次之后的答案为$ans_i$,分别考虑每个元素对ans数组的贡献 若$s_i& ...
- JZOJ 【NOIP2017提高A组模拟9.14】捕老鼠
JZOJ [NOIP2017提高A组模拟9.14]捕老鼠 题目 Description 为了加快社会主义现代化,建设新农村,农夫约(Farmer Jo)决定给农庄里的仓库灭灭鼠.于是,猫被农夫约派去捕 ...
- JZOJ 5246. 【NOIP2017模拟8.8A组】Trip(trip)
5246. [NOIP2017模拟8.8A组]Trip(trip) (File IO): input:trip.in output:trip.out Time Limits: 1500 ms Memo ...
- JZOJ 5235. 【NOIP2017模拟8.7A组】好的排列
5235. [NOIP2017模拟8.7A组]好的排列 (File IO): input:permutation.in output:permutation.out Time Limits: 1000 ...
- JZOJ 5230. 【NOIP2017模拟A组模拟8.5】队伍统计
5230. [NOIP2017模拟A组模拟8.5]队伍统计 (File IO): input:count.in output:count.out Time Limits: 1500 ms Memory ...
- JZOJ【NOIP2013模拟联考14】隐藏指令
JZOJ[NOIP2013模拟联考14]隐藏指令 题目 Description 在d维欧几里得空间中,指令是一个长度为2N的串.串的每一个元素为d个正交基的方向及反方向之一.例如,d = 1时(数轴) ...
- JZOJ.5281【NOIP2017模拟8.15】钦点
Description
- [jzoj 5178] [NOIP2017提高组模拟6.28] So many prefix? 解题报告(KMP+DP)
题目链接: https://jzoj.net/senior/#main/show/5178 题目: 题解: 我们定义$f[pos]$表示以位置pos为后缀的字符串对答案的贡献,答案就是$\sum_{i ...
随机推荐
- 后台dubug有值且sql也打印出来执行了但是前台就是查不到数据
记录在sturts2里面 摔得最深的一次 public String queryJoinAccount(){ //用来存储分页的数据 pageMap=new HashMap<String, Ob ...
- bootstrap 页面标题
页面标题会突出显示,当一个网页中有多个标题且每个标题之间需要添加一定的间距时,页面标题显得特别有用,页面标题会给不是页面标题之间的元素加上横线 加以区分,以突出标题显示. 页面标题类 显示效果图 代码 ...
- easy ui datagrid 数据分页
参照easyui官方网站提供的demo写了个datagrid数据分页的demo, 具体参数我就不一一罗列了,详细见官方网站, 这里只介绍一下具体的注意事项和常乃用到的几项, $('#test').da ...
- golang的各种数据格式的互相转换
int to string import ( "strconv" ) int i = 10 str1 := strconv.Itoa(i) struct to json impor ...
- 阿里云web播放器
原文地址:https://help.aliyun.com/document_detail/51991.html?spm=5176.doc61109.6.703.ZTCYoi 一.概念说明 1. pla ...
- Nodejs 命令行交互神奇 yargs
传送门: # example https://github.com/yargs/yargs/blob/master/docs/examples.md # 官网 http://yargs.js.org/ ...
- JVM虚拟机(二):堆、栈、方法区概念区别
Java 堆 Java堆是和Java应用程序关系最密切的内存空间,几乎所有的对象都放在其中,并且Java堆完全是自动化管理,通过垃圾收集机制,垃圾对象会自动清理,不需自己去释放. 根据垃圾回收机制的不 ...
- Linux学习一
1.Linux的优缺点: 长处: 稳定的系统 免费或少许费用 安全性,漏洞的高速修补 多任务,多用户 用户与用户的规划 相对不耗资源的系统 适合须要小内核的嵌入式系统 整合度佳且多样的图形用户界面 缺 ...
- atitit.提取zip rar文件列表 java php c# 的原理与设计
atitit.java提取zip rar文件列表 1. 取zip rar文件的场景问题 1 1.1. 多重压缩的问题 1 1.2. 文件名编码的问题 1 1.3. 目录的判定 1 2. rar的解析 ...
- (3)Smali系列学习之Smali语法详解
数据类型 Dalvik字节码只有两种格式:基本类型和引用类型.对象和数组属于引用类型 语法 含义 V void,只用于返回值类型 Z boolean B byte S short C char I i ...
