「雅礼集训 2017 Day2」线段游戏（线段树懒标记“启发式下传”，李超树）

题面

题解

加入一条线段，可以把它转化为在[L,R]区间内加一条线 y=ax+b （如果原线段与y轴平行，就相当于在{x1}处加一条线 y=max(y1,y2)）

我们可以把它加到线段树上，线段树上每个点存一个区间内贯穿整个区间的一条对答案有贡献的线段（因为是贯穿整个区间，所以存一个 {a,b} 表示 y=ax+b 就行了）。

一条线段是这么加上去的：

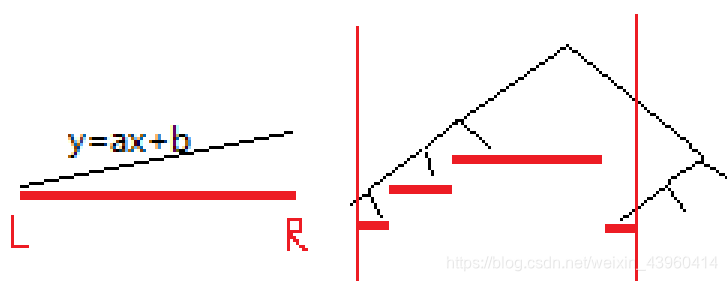
查询要遍历路径上的所有点：

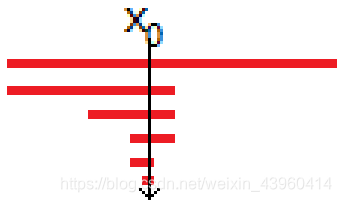
接下来，最大的问题就是，它会产生冲突！

当我们加一条线段到线段树上，而原来节点上就已经有了一条线段怎么办？

首先，如果其中一条线段凌驾于另一条之上，肯定直接判了嘛，

但是，出问题的就是两条线段交叉，

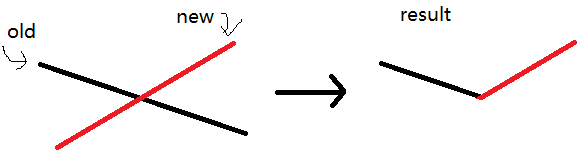
而线段树上的节点存不了“V”字形，也维护不了（除了写平衡树的大佬）

这里就要用到一个“启发式下传”的思想

一般的暴力想法就是先把原来的线段先下传了，再把新线段放上去：

稍微有点想法的人会先把“V”字形处理出来，并把两条线段拆开下传（虽然并没有什么*用）：

这时候，较聪明的人就会想，为什么原来的地方要空着呢？把其中随便一条线段留在原处，对答案也没有影响，但是却快得多：

最后，深谙暴力优化精髓的人会想，数据肯定会卡每次下传的线段长度只比原先段短一点的情况，便把“V”字形两条线段中短的一条下传，

于是便优化出了正解：

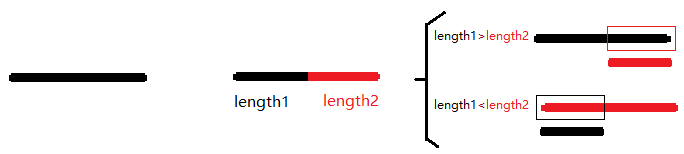
我们会发现，每次一旦冲突，便会开始下传，每次下传的线段长度至少会减半，所以，下传复杂度为O(log)，加线段复杂度就为O(log^2)

查询复杂度没变，总复杂度就为O(mlog^2)

CODE

#include<map>
#include<queue>
#include<cmath>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXN 50005
#define MAXM 100005
#define LL long long
#define DB double
#define ENDL putchar('\n')
#define lowbit(x) ((-x)&(x))
//#define int LL
//#pragma GCC optimize(2)
LL read() {
    LL f = 1,x = 0;char s = getchar();
    while(s < '0' || s > '9') {if(s=='-')f=-f;s = getchar();}
    while(s >= '0' && s <= '9') {x=x*10+(s-'0');s=getchar();}
    return f*x;
}
const int MOD = 998244353;
int n,m,i,j,s,o,k;
struct it{
	DB x,y;
	it(){x = y = 0;}
	it(DB X,DB Y){x=X;y=Y;}
};
it cg(it a,it b) {
	DB k = (a.y - b.y) / (a.x - b.x);
	DB B = a.y - a.x * k;
	return it(k,B);
}
it jd(it a,it b) {
	DB xx = (b.y - a.y) / (a.x - b.x);
	return it(xx,a.x*xx+a.y);
}
bool abov(it a,it st) {
	DB y2 = a.x * st.x + st.y;
	return a.y >= y2;
}
bool operator < (it a,it b) {return a.y < b.y;}
bool operator > (it a,it b) {return b < a;}
bool operator <= (it a,it b) {return a.y <= b.y;}
bool operator >= (it a,it b) {return b <= a;}
struct tr{
	int l,r;
	it st;
	tr(){l=r=0;st=it(0,-1e9);}
}tre[MAXM<<4];
void maketree(int a,int l,int r) {
	tre[a].l = l;tre[a].r = r;
	if(l < r) {
		int mid = (l+r)>>1;
		maketree(a<<1,l,mid);
		maketree(a<<1|1,mid+1,r);
	}
	return ;
}
void addtree(int a,int l,int r,it st) {
	if(tre[a].l > r || tre[a].r < l) return ;
	if(tre[a].l >= l && tre[a].r <= r) {
		DB ll = (DB)tre[a].l,rr = (DB)tre[a].r;
		it l1 = it(ll,ll*tre[a].st.x+tre[a].st.y);
		it r1 = it(rr,rr*tre[a].st.x+tre[a].st.y);
		it l2 = it(ll,ll*st.x+st.y),r2 = it(rr,rr*st.x+st.y);
		if(l1 >= l2 && r1 >= r2) return ;
		if(l2 >= l1 && r2 >= r1) {
			tre[a].st = st; return ;
		}
		it md = jd(st,tre[a].st); int mid = (tre[a].l+tre[a].r)>>1;
		it ls = (l1 >= l2 ? tre[a].st:st),rs = (r1 >= r2 ? tre[a].st:st);
		if(md.x <= (DB)mid) tre[a].st = rs,addtree(a<<1,l,r,ls);
		else tre[a].st = ls,addtree(a<<1|1,l,r,rs);
		return ;
	}
	addtree(a<<1,l,r,st);addtree(a<<1|1,l,r,st);
	return ;
}
DB query(int a,int ad) {
	if(tre[a].l > ad || tre[a].r < ad) return -1e9;
	if(tre[a].l == tre[a].r) {
		return ad*tre[a].st.x + tre[a].st.y;
	}
	return max(ad*tre[a].st.x+tre[a].st.y,max(query(a<<1,ad),query(a<<1|1,ad)));
}
int main() {
	n = read();m = read();
	maketree(1,1,100000);
	for(int i = 1;i <= n;i ++) {
		it a,b;
		a.x = (DB)read();
		a.y = (DB)read();
		b.x = (DB)read();
		b.y = (DB)read();
		if(a.x > b.x) swap(a,b);
		it st;
		if(a.x == b.x) st = it(0,max(a.y,b.y));
		else st = cg(a,b);
		int ll = (int)a.x,rr = (int)b.x;
		addtree(1,ll,rr,st);
	}
	for(int i = 1;i <= m;i ++) {
		k = read();
		if(!k) {
			it a,b;
			a.x = (DB)read();
			a.y = (DB)read();
			b.x = (DB)read();
			b.y = (DB)read();
			if(a.x > b.x) swap(a,b);
			it st;
			if(a.x == b.x) st = it(0,max(a.y,b.y));
			else st = cg(a,b);
			int ll = (int)a.x,rr = (int)b.x;
			addtree(1,ll,rr,st);
		}
		else {
			int x0 = read();
			DB ans = query(1,x0);
			printf("%.4f\n",ans < -1e8 ? 0.0:ans);
		}
	}
    return 0;
}