打地鼠（susliks） 方法记录

[SDOI2011]打地鼠

题目描述

2020.4.29 数据更新。

打地鼠是这样的一个游戏：地面上有一些地鼠洞，地鼠们会不时从洞里探出头来很短时间后又缩回洞中。玩家的目标是在地鼠伸出头时，用锤子砸其头部，砸到的地鼠越多分数也就越高。

游戏中的锤子每次只能打一只地鼠，如果多只地鼠同时探出头，玩家只能通过多次挥舞锤子的方式打掉所有的地鼠。你认为这锤子太没用了，所以你改装了锤子，增加了锤子与地面的接触面积，使其每次可以击打一片区域。如果我们把地面看做 \(m\times n\) 的方阵，其每个元素都代表一个地鼠洞，那么锤子可以覆盖 \(r\times c\) 区域内的所有地鼠洞。但是改装后的锤子有一个缺点：每次挥舞锤子时，对于这的区域中的所有地洞，锤子会打掉恰好一只地鼠。也就是说锤子覆盖的区域中，每个地洞必须至少有 \(1\) 只地鼠，且如果某个地洞中地鼠的个数大于 \(1\)，那么这个地洞只会有 \(1\) 只地鼠被打掉，因此每次挥舞锤子时，恰好有\(r\times c\) 只地鼠被打掉。由于锤子的内部结构过于精密，因此在游戏过程中你不能旋转锤子（即不能互换 \(r\) 和 \(c\)）。

你可以任意更改锤子的规格(即你可以任意规定 \(r\) 和 \(c\) 的大小)，但是改装锤子的工作只能在打地鼠前进行(即你不可以打掉一部分地鼠后，再改变锤子的规格)。你的任务是求出要想打掉所有的地鼠，至少需要挥舞锤子的次数。

Hint：由于你可以把锤子的大小设置为 \(1\times 1\)，因此本题总是有解的。

输入格式

第一行包含两个正整数 \(m\) 和 \(n\)；

下面 \(m\) 行每行 \(n\) 个正整数描述地图，每个数字表示相应位置的地洞中地鼠的数量。

输出格式

输出一个整数，表示最少的挥舞次数。

样例 #1

样例输入 #1

3 3
1 2 1
2 4 2
1 2 1

样例输出 #1

4

提示

【样例说明】

使用 \(2\times 2\) 的锤子，分别在左上、左下、右上、右下挥舞一次。

【数据规模和约定】

对于 \(30\%\) 的数据，\(m\), \(n\leq 5\) ；

对于 \(60\%\) 的数据，\(m\), \(n\leq 30\) ；

对于 \(100\%\) 的数据，\(1\leq m\), \(n\leq 100\) ，其他数据不小于 \(0\)，不大于 \(10^5\) 。

题解

最暴力的想法：枚举法

先枚举锤子的长与宽（2层循环）；

再枚举锤子敲的位置（2层循环）；

下一步就该判断落锤是否合理合法，具体地，有两种思路。

思路1

假如有一个\(2\times2\)的锤子要砸击下面这个区域（展示的是全图的一部分）。

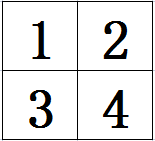
对于每一次砸击，我们将被砸区域的每个数减\(1\),直到区域中有任何一个数被减至\(0\)，（时间复杂度为：区间内元素的个数\(\times\)砸到有任何一个数变成\(0\)的次数）然后继续枚举下一个要砸的区域。下图中，黄色区域是正准备受砸的区域，红字是上一次砸完后的结果。

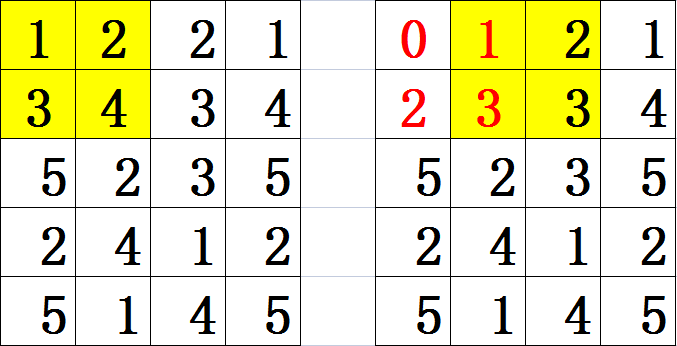
将每个能砸的区域都枚举完毕后，再判断一下全图中是否还有元素未被清零。若有，则说明这个型号的锤子无法满足要求，否则，计入最小答案。

思路2

假如有一个\(2\times2\)的锤子要砸击下面这个区域（展示的是全图的一部分）。

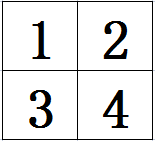
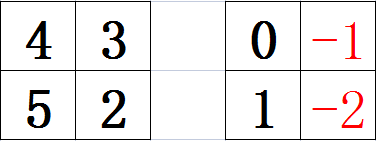
一次性砸多次，砸的次数是区域左上角的数大小。（即将左上角的数清零）下图展示按此方法砸前砸后的变化。

但是，如果出现下面这种，左上角的数清零导致区域内其它数变成负数的情况，就可以直接判断出这种型号的锤子无法满足要求，然后直接枚举下一种锤子的型号。

若有一种型号的锤子能锤遍全图，我们再判断一下全图中是否还有元素未被清零。若有，则说明这个型号的锤子无法满足要求，否则，计入最小答案。

显然，由于思路2需要枚举的砸击次数少，且能及时排除不合要求的锤子，所以思路2更优

然后再考虑其它优化手段。

假设一把 \(r\times c\) 的锤子是合格的，它需要砸 \(x\) 次，那么它总共砸毙的地鼠数 \(sum=r\times c\times x\) ，这个\(sum\) 我们可以事先统计出来，即全部地洞里的地鼠数量之和。

换个角度来想，我们已经统计出 \(sum\) ，现在正在枚举 \(i\times j\) 型号的锤子。若这种锤子满足要求，就应该满足：\(sum\) 是\(i\times j\) 的整数倍。在此基础上再判断该型号的锤子能否锤尽全图地鼠，若能，则答案 \(ans=sum/i/j\) .可以节省不少时间。这里枚举 \(i\) 和 \(j\) ,就可以从\(1\)~\(n\) 进行，这样 \(i\) 和 \(j\) 越枚举越大，\(ans\) 也就越来越小，省去了比较大小的过程。

除此之外我们还可以进行剪枝。

若当前的 \(sum/i/j\) 小于已经算出来的 \(ans\) ，则当前情况必不可能为最优情况。

AC代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=105;
int a[N][N],b[N][N],n,m,ans,sum;
bool check(int x,int y)
{
	memcpy(b,a,sizeof(a));
	for(int i=1;i<=n-x+1;i++)
	{
		for(int j=1;j<=m-y+1;j++)
		{
			if(b[i][j])
			{
				int z=b[i][j];
				for(int k=0;k<x;k++)
				{
					for(int l=0;l<y;l++)
					{
						b[i+k][j+l]-=z;
						if(b[i+k][j+l]<0) return 0;
					}
				}
			}
		}
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			if(b[i][j]) return 0;
		}
	}
	return 1;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			scanf("%d",&a[i][j]);
			sum+=a[i][j];
		}
	}
	ans=sum;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			if(sum%(i*j)==0&&sum/i/j<ans)
			{
				if(check(i,j)) ans=sum/i/j;
			}
		}
	}
	printf("%d\n",ans);
	return 0;
}