Codeforces 599D Spongebob and Squares（数学）

D. Spongebob and Squares

Spongebob is already tired trying to reason his weird actions and calculations, so he simply asked you to find all pairs of n and m, such that there are exactly x distinct squares in the table consisting of n rows and m columns. For example, in a 3 × 5 table there are 15squares with side one, 8 squares with side two and 3 squares with side three. The total number of distinct squares in a 3 × 5 table is15 + 8 + 3 = 26.

Input

The first line of the input contains a single integer x (1 ≤x≤ 1018) — the number of squares inside the tables Spongebob is interested in.

Output

First print a single integer k — the number of tables with exactly x distinct squares inside.

Then print k pairs of integers describing the tables. Print the pairs in the order of increasing n, and in case of equality — in the order of increasing m.

Sample test(s)

input

26

output

6

1 26

2 9

3 5

5 3

9 2

26 1

input

2

output

2

1 2

2 1

input

8

output

4

1 8

2 3

3 2

8 1

来自 <http://codeforces.com/problemset/problem/599/D>

Codeforces Round #332 (Div. 2)

【题意】：

对于给定的X，找出所有的 M*N 矩阵，使得其中恰含 X 个正方形

【解题思路】：

主要是推公式。

对于给定的M N：

S = M*N + (M-1)*(N-1) + …… 直至其中一项变0；

以上公式展开并求和可得：

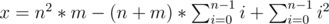
而右边这几项都可以直接求出，

X = m*n*b - (m+n)*(m-1)*m/2 + (2*m-1)*m*(m-1)/6;（m<n）

可知上述 N 可用X和M来线性表示：

故枚举其中一项，利用公式求另一项即可；

注意还要判重和排序，这里直接用set就可以了。

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<vector>
 #include<algorithm>
 #include<set>
 #define inf 0x3f3f3f3f
 #define LL long long
 #define maxn 2100000
 #define IN freopen("in.txt","r",stdin);
 using namespace std;

 LL sum;
 LL a, b;
 struct node{
     LL a,b;
     node(LL _a,LL _b) {a=_a;b=_b;}
     bool operator <(const node& c)const{
         return a<c.a||a==c.a&&b<c.b;
     }
 };
 set<node> ans;

 LL check(LL a, LL b)
 {
     return a*a*b - (a+b)*(a-)*a/ + (*a-)*a*(a-)/;
 }
 LL cal(LL a)
 {
     return (*sum-a+a*a*a)/(*a*a+*a);
 }

 int main(int argc, char const *argv[])
 {
     //IN;

     while(scanf("%I64d",&sum)!=EOF)
     {
         ans.clear();
         for(a=; a<=maxn; a++) {
             b = cal(a);

             if(check(min(a,b),max(a,b)) != sum) continue;

             ans.insert(node(a,b));
             if(a!=b) ans.insert(node(b,a));
         }

         int cnt = ans.size();
         //sort(ans.begin(),ans.end());
         printf("%d\n",cnt);
         set<node>::iterator it;
         for(it=ans.begin();it!=ans.end();it++){
             printf("%I64d %I64d\n",(*it).a,(*it).b);
         }
     }

     return ;
 }