AVL树的插入操作(旋转)图解
AVL树的概念
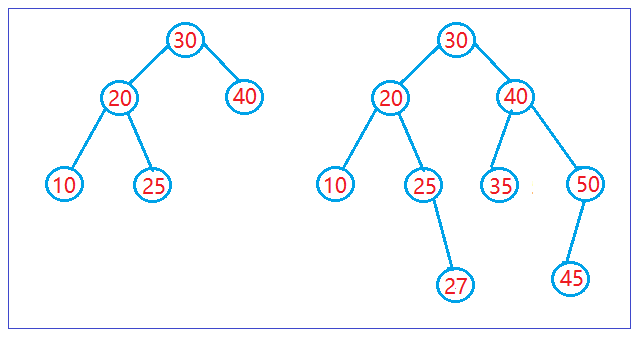

AVL树的插入
template<class K>
struct AVLTreeNode
{
K _key;
int _bf;
AVLTreeNode<K, V>* _left;
AVLTreeNode<K, V>* _right;
AVLTreeNode<K, V>* _parent; AVLTreeNode(const K& key, const V& value)
:_key(key),
_bf(),
_left(NULL),
_right(NULL),
_parent(NULL)
{}
};

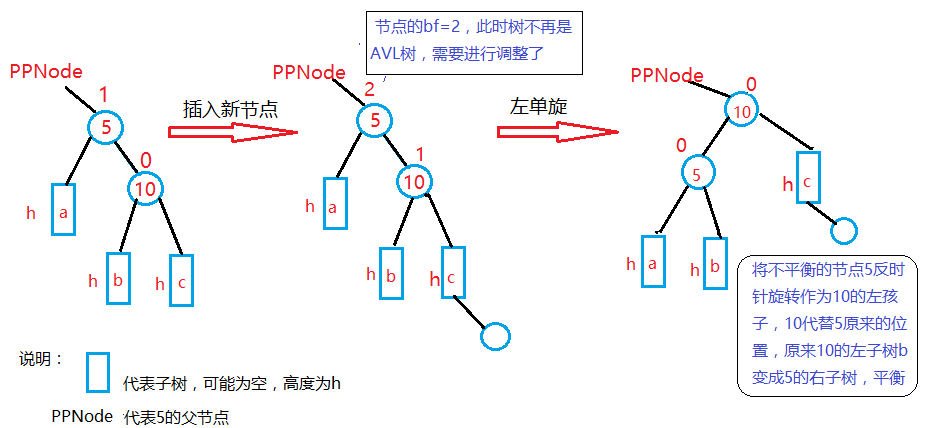

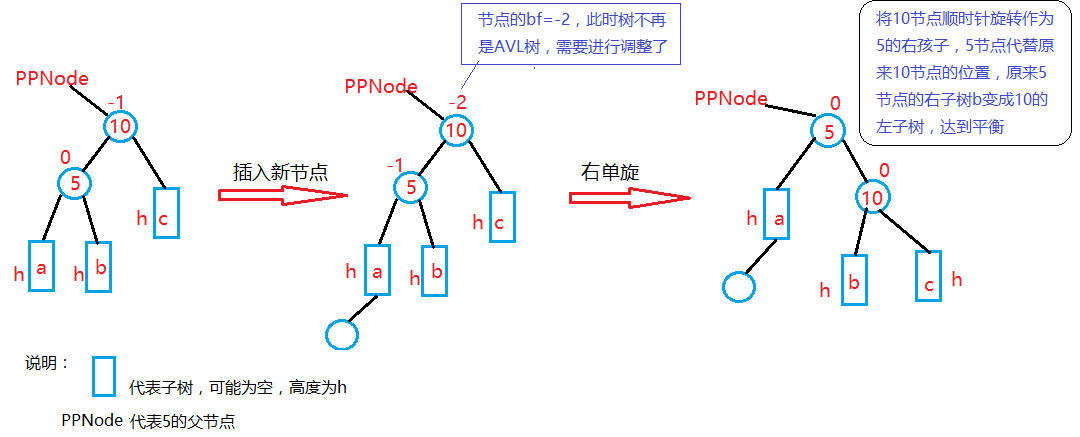
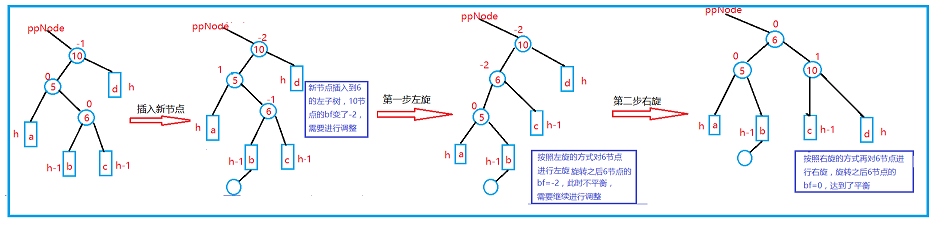




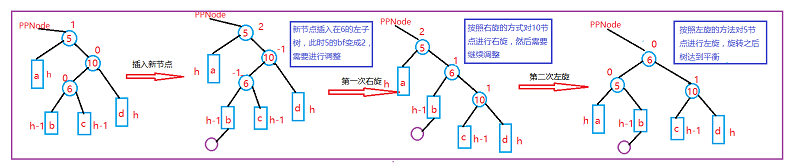
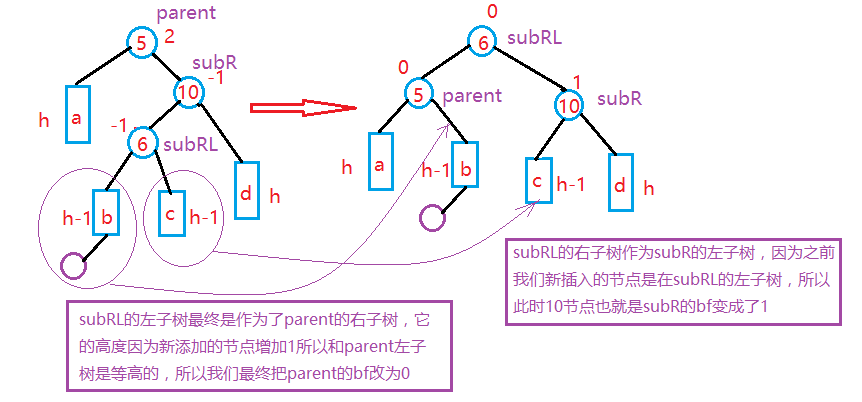

程序代码:
bool Insert(const K& key, const V& value)
{
if (_root == NULL)
{
_root = new Node(key, value);
return true;
}
Node* pcur = _root;
Node* parent = NULL;
while (pcur)
{
if (pcur->_key == key)
return false;
else if (pcur->_key < key)
{
parent = pcur;
pcur = pcur->_right;
}
else
{
parent = pcur;
pcur = pcur->_left;
}
}
if (parent->_key < key)
{
pcur = parent->_right = new Node(key, value);
pcur->_parent = parent;
}
else
{
pcur = parent->_left = new Node(key, value);
pcur->_parent = parent;
} while (parent)
{
//修正平衡因子
if (pcur == parent->_left)
{
parent->_bf--;
}
if (pcur == parent->_right)
{
parent->_bf++;
}
//
if (parent->_bf == )
break;
else if (parent->_bf == - || parent->_bf == )
{
pcur = parent;
parent = pcur->_parent;
}
else //parent->bf -2 || 2
{ if (parent->_bf == -)
{
if (pcur->_bf == -) //右单旋
RotateR(parent);
else //左右双旋
RotateLR(parent);
}
else
{
if (pcur->_bf == ) //左单旋
RotateL(parent);
else //右左双旋
RotateRL(parent);
}
break;
}
}
return true;
}
>>旋转
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
//换指向
parent->_left = subLR;
subL->_right = parent; if (subLR)
{
subLR->_parent = parent;
} Node* PParent = parent->_parent; //判断parent是否有父节点
if (PParent)
{
if (parent == PParent->_left)
{
PParent->_left = subL;
subL->_parent = PParent;
}
else
{
PParent->_right = subL;
subL->_parent = PParent;
}
}
else
{
_root = subL;
subL->_parent = NULL;
}
parent->_parent = subL;
//修改bf
subL->_bf = ;
parent->_bf = ;
} //
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
//调整指向
subR->_left=parent;
parent->_right = subRL; if (subRL) //如果subRL非空
{
subRL->_parent = parent;
} Node* PPNode = parent->_parent;
if (PPNode)
{
if (PPNode->_left == parent)
PPNode->_left = subR;
else
PPNode->_right = subR; //subR的父节点改变
subR->_parent = PPNode;
}
else
{
_root = subR; //根节点
subR->_parent = NULL;
}
parent->_parent = subR;
/*修改bf*/
parent->_bf = subR->_bf = ;
} //双旋(左右、、右左)
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf; RotateR(parent->_right);
RotateL(parent); //调整subR和parent的平衡因子
if (bf == -)
subR->_bf = ; // subR的bf在左旋中已经置0了,这里就没有再写
else if (bf == )
parent->_bf = -; else
{
parent->_bf = ;
subRL->_bf = ;
}
} void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf;
RotateL(parent->_left);
RotateR(parent); //调整parent和subL的平衡因子
if (bf == -)
parent->_bf = ; //subL的bf在左旋中已经置0了,这里就没有再写
else if (bf == )
subL->_bf = -; //parent的bf在左旋中已经置0了
else
{
subL->_bf = ;
parent = ;
}
}
AVL树的插入操作(旋转)图解的更多相关文章
- AVL树的插入和删除
一.AVL 树 在计算机科学中,AVL树是最早被发明的自平衡二叉查找树.在AVL树中,任一节点对应的两棵子树的最大高度差为 1,因此它也被称为高度平衡树.查找.插入和删除在平均和最坏情况下的时间复杂度 ...
- AVL 树的插入、删除、旋转归纳
参考链接: http://blog.csdn.net/gabriel1026/article/details/6311339 1126号注:先前有一个概念搞混了: 节点的深度 Depth 是指从根 ...
- AVL树的单双旋转操作
把必须重新平衡的节点称为å.对于二叉树,å的两棵子树的高度最多相差2,这种不平衡可能有四种情况: 对å的左儿子的左子树进行插入节点(左-左) 对å的左儿子的右子树进行插入节点(左-右) 对å的右儿子的 ...
- AVL树的插入删除查找算法实现和分析-1
至于什么是AVL树和AVL树的一些概念问题在这里就不多说了,下面是我写的代码,里面的注释非常详细地说明了实现的思想和方法. 因为在操作时真正需要的是子树高度的差,所以这里采用-1,0,1来表示左子树和 ...
- AVL树的插入与删除
AVL 树要在插入和删除结点后保持平衡,旋转操作必不可少.关键是理解什么时候应该左旋.右旋和双旋.在Youtube上看到一位老师的视频对这个概念讲解得非常清楚,再结合算法书和网络的博文,记录如下. 1 ...
- 第七章 二叉搜索树 (d2)AVL树:插入
- 创建AVL树,插入,删除,输出Kth Min
https://github.com/TouwaErioH/subjects/tree/master/C%2B%2B/PA2 没有考虑重复键,可以在结构体内加一个int times. 没有考虑删除不存 ...
- 数据结构--Avl树的创建,插入的递归版本和非递归版本,删除等操作
AVL树本质上还是一棵二叉搜索树,它的特点是: 1.本身首先是一棵二叉搜索树. 2.带有平衡条件:每个结点的左右子树的高度之差的绝对值最多为1(空树的高度为-1). 也就是说,AVL树,本质上 ...
- AVL树(查找、插入、删除)——C语言
AVL树 平衡二叉查找树(Self-balancing binary search tree)又被称为AVL树(AVL树是根据它的发明者G. M. Adelson-Velskii和E. M. Land ...
随机推荐
- HDU-4737 A Bit Fun 维护
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4737 题意:给一个数列a0, a1 ... , an-1,令 f(i, j) = ai|ai+1|ai ...
- 转】Nginx+tomcat集群环境搭建(Windows下)
原博文出自于: http://blog.csdn.net/clj198606061111/article/details/22621003 感谢! 实验环境 windows xp s ...
- 最新CentOS6.x下redis安装
1:软件环境: 系统版本:CentOS release 6.5 redis版本:redis-cli 3.0.5 安装目录:"/usr/local/redis" 下载软件:" ...
- setbuf和freopen
看memcached代码的时候学习了一个api,setbuf,可以设置文件流的缓冲区. #include <stdio.h> void setbuf(FILE *stream ...
- 工具栏停靠实现(toolbar docking)
// TODO: 如果不需要工具栏可停靠,则删除这三行 m_ToolBar_File.EnableDocking(CBRS_ALIGN_ANY); EnableDocking(CBRS_ALIGN_A ...
- 33条C#、.Net经典面试题目及答案[zt]
33条C#..Net经典面试题目及答案[zt] 本文集中了多条常见的C#..Net经典面试题目例如“.NET中类和结构的区别”.“ASP.NET页面之间传递值的几种方式?”,并简明扼要的给出了答案,希 ...
- mysql与java数据类型对照
类型名称 显示长度 数据库类型 JAVA类型 JDBC类型索引(int) 描述 VARCHAR L+N VARCHAR java.lang.String 12 CHAR N CHAR java.lan ...
- iOS UIButton EdgeInsets
说一下系统的button,image 和 title的位置关系 默认image 和 title的位置关系: 随便画了草图,有点丑,不过不妨碍理解: 第一种:在button上只设置文字,这个时候,but ...
- 修改 SVN 账户密码的方法
记是记不住 的,即便是每天都在用的东西,也有貌似熟悉其实很陌生的时候,或者说根本就是不熟悉.于是需要拿出来经常翻翻,比如我们的SVN账户配置,很简单的一个 case,你可能是svn使用高手,但不一定记 ...
- 在WCF中不使用svc文件直接使用cs文件
在 配置中有个节点可以实现 此功能 <serviceHostingEnvironment multipleSiteBindingsEnabled="true" > &l ...
