Julia - 复数

全局变量 im 即复数 i ，为复数的虚数单位，表示 -1 的正平方根

Julia 允许数值作为代数系数，这也适用于复数

julia> 1 + 2im
1 + 2im

复数的运算

julia> (1 + 2im) + (2 - 3im)
3 - 1im

julia> (1 + 2im) - (2 - 3im)
-1 + 5im

julia> (1 + 2im) * (2 - 3im)
8 + 1im

julia> (1 + 2im) / (2 - 3im)
-0.30769230769230776 + 0.5384615384615384im

julia> (1 + 2im)^2
-3 + 4im

julia> (1 + 2im)^(2 - 3im)
135.7449526364423 - 27.496999408173988im

julia> 3(1 + 2im)  # 等于 3 * (1 + 2im)
3 + 6im

julia> 2 + (1 + 2im)
3 + 2im

julia> 2im + (1 + 2im)
1 + 4im

real() 函数获取复数的实部大小

julia> real(1 + 2im)
1

julia> real(2im)
0

imag() 函数获取复数的虚部大小

julia> imag(1 + 2im)
2

julia> imag(1)
0

conj() 函数求复数的共轭复数

julia> conj(1 + 2im)
1 - 2im

julia> conj(2im)
0 - 2im

abs() 函数求复数的模

对于复数 z = a + bi，模为：

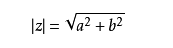
julia> abs(1 + 2im)
2.23606797749979

julia> abs(2im)
2.0

abs2() 函数求复数模的平方

julia> abs2(1 + 2im)
5

angle() 函数返回弧度制的相位

julia> angle(1 + 2im)
1.1071487177940904

complex() 函数用于创建复数

julia> complex(1, 2)  # 创建实部为 1，虚部为 2 的复数
1 + 2im

julia> a = 1;b = 2;complex(a, b)  # 用变量来创建复数
1 + 2im

Inf 和 NaN 也用来可以构造复数

julia> 1 + Inf*im
1.0 + Inf*im

julia> 1 + NaN*im
1.0 + NaN*im