【BZOJ 2436】 2436: [Noi2011]Noi嘉年华 （区间DP）

2436: [Noi2011]Noi嘉年华

Description

NOI2011 在吉林大学开始啦！为了迎接来自全国各地最优秀的信息学选手，
吉林大学决定举办两场盛大的 NOI 嘉年华活动，分在两个不同的地点举办。每
个嘉年华可能包含很多个活动，而每个活动只能在一个嘉年华中举办。 
现在嘉年华活动的组织者小安一共收到了 n个活动的举办申请，其中第 i 个
活动的起始时间为 Si，活动的持续时间为Ti。这些活动都可以安排到任意一个嘉
年华的会场，也可以不安排。 
小安通过广泛的调查发现，如果某个时刻，两个嘉年华会场同时有活动在进
行（不包括活动的开始瞬间和结束瞬间），那么有的选手就会纠结于到底去哪个
会场，从而变得不开心。所以，为了避免这样不开心的事情发生，小安要求不能
有两个活动在两个会场同时进行（同一会场内的活动可以任意进行）。 
另外，可以想象，如果某一个嘉年华会场的活动太少，那么这个嘉年华的吸
引力就会不足，容易导致场面冷清。所以小安希望通过合理的安排，使得活动相
对较少的嘉年华的活动数量最大。 
此外，有一些活动非常有意义，小安希望能举办，他希望知道，如果第i 个
活动必须举办（可以安排在两场嘉年华中的任何一个），活动相对较少的嘉年华
的活动数量的最大值。

Input

输入的第一行包含一个整数 n，表示申请的活动个数。 
接下来 n 行描述所有活动，其中第 i 行包含两个整数 Si、Ti，表示第 i 个活
动从时刻Si开始，持续 Ti的时间。

Output

输出的第一行包含一个整数，表示在没有任何限制的情况下，活动较少的嘉
年华的活动数的最大值。 
接下来 n 行每行一个整数，其中第 i 行的整数表示在必须选择第 i 个活动的
前提下，活动较少的嘉年华的活动数的最大值。

Sample Input

5
8 2
1 5
5 3
3 2
5 3

Sample Output

2
2
1
2
2
2

HINT

在没有任何限制的情况下，最优安排可以在一个嘉年华安排活动 1, 4，而在

另一个嘉年华安排活动 3, 5，活动2不安排。

1≤n≤200 0≤Si≤10^9

1≤Ti≤ 10^9

Source

Day2

【分析】

　　怎么说，又不会做。。

　　这个两个东东的最小值最大不会搞，额，当然这里是不能二分的嘛。。

　　也不会在DP中记录，然后题解的方法好像。。称呼其为“定一议二”？就是DP中有一维说的是其中一个人拿了x个区间的情况下，另一个人最多拿多少区间。【很对吧!

　　这样子应该是会做第一问了的，n^3DP就可以过。

　　但是后面，一个东西必须做的，就会感觉要n^4吧。

　　但是有类似单调性的东西，这个后面再详细讲，网上他们都没有仔细说，我是自己推了一下的。

　　先看这个大神的详细题解，这个写得真的很清晰很好懂啊！

　　

　　来自：http://blog.csdn.net/qpswwww/article/details/45251877

　　然后说说那个什么递增单凸的。

　　首先，显然pre[][x]和suf[][y]都是递减的。

　　对于x确定，y在变，f[x][y]=min(x+y,pre[i][x]+num[i][j]+suf[j][y]),显然x+y随y递增而增，pre[i][x]+num[i][j]+suf[j][y]随y递增而减。

　　

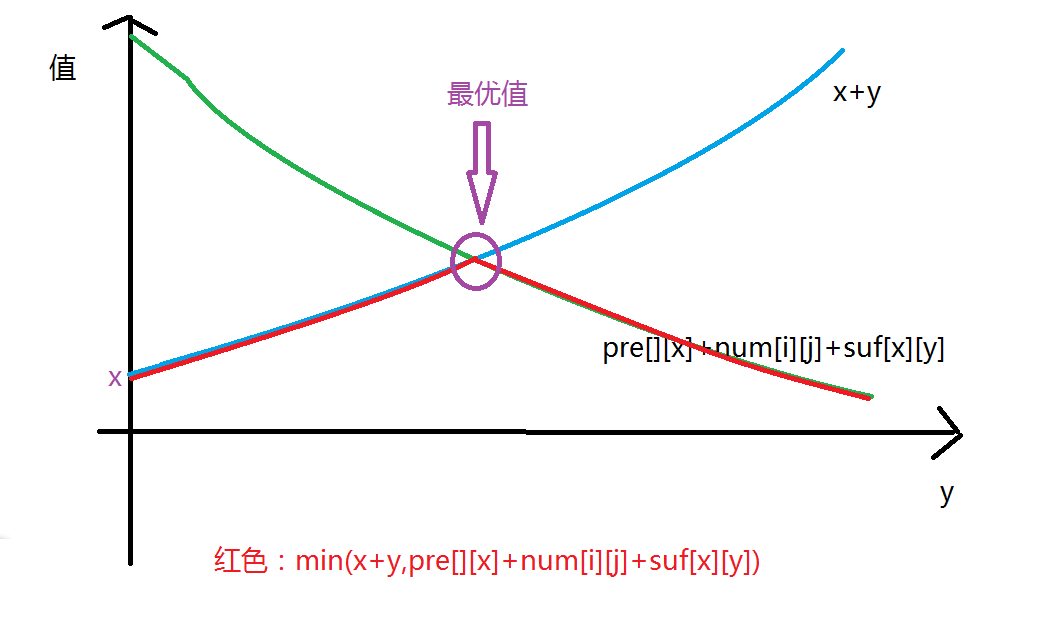
　　就是这样的，下面标红的函数就是真正的函数，显然是上凸的了。

　　所以程序里面y按顺序，找到一个now<当前最优值 就可以break了。

　　然后说明一个就是随着x的增加，取最优值的y单调递减。这个画个图也可以看出来了。

　　

　　所以就是这样做了，y这里均摊的话，就是O(n^3)

　　【调了一晚上好内伤，我好蠢啊。。

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 using namespace std;
 #define Maxn 210
 #define INF 0xfffffff

 int n,p;
 int mymax(int x,int y) {return x>y?x:y;}
 int mymin(int x,int y) {return x<y?x:y;}

 int s[Maxn],t[Maxn],num[*Maxn][*Maxn];
 int pre[*Maxn][*Maxn],suf[*Maxn][*Maxn],f[*Maxn][*Maxn];

 struct node {int x,y;}a[*Maxn];
 bool cmp(node x,node y) {return x.x<y.x;}

 void init()
 {
     scanf("%d",&n);
     for(int i=;i<=n;i++)
     {
         scanf("%d%d",&s[i],&t[i]);
         t[i]+=s[i];
         a[i*-].x=s[i];a[i*-].y=i;
         a[i*].x=t[i];a[i*].y=-i;
     }
     sort(a+,a++n*,cmp);
     p=;
     for(int i=;i<=n*;i++)
     {
         if(i==||a[i].x!=a[i-].x) p++;
         if(a[i].y>) s[a[i].y]=p;
         else t[-a[i].y]=p;
     }
     memset(num,,sizeof(num));
     memset(pre,,sizeof(pre));
     memset(suf,,sizeof(suf));
     for(int i=;i<=p;i++)
      for(int j=i;j<=p;j++)
       for(int k=;k<=n;k++) if(s[k]>=i&&t[k]<=j) num[i][j]++;

     for(int i=;i<=p;i++)
      for(int j=;j<=n;j++)
       for(int k=;k<=i;k++)
       {
           if(j>num[][i]) {pre[i][j]=-INF;continue;}
           pre[i][j]=mymax(pre[i][j],pre[k][j]+num[k][i]);
           if(j>=num[k][i]) pre[i][j]=mymax(pre[i][j],pre[k][j-num[k][i]]);
       }//printf("\n");
     for(int i=p;i>=;i--)
      for(int j=;j<=n;j++)
       for(int k=i;k<=p;k++)
       {
           if(j>num[i][p]) {suf[i][j]=-INF;continue;}
           suf[i][j]=mymax(suf[i][j],suf[k][j]+num[i][k]);
           if(j>=num[i][k]) suf[i][j]=mymax(suf[i][j],suf[k][j-num[i][k]]);
       }
 }

 int main()
 {
     init();

     int ans=;
     for(int i=;i<=p;i++)
      for(int j=i;j<=p;j++)
      {
         int y=num[j][p];
         for(int x=;x<=num[][i];x++)
         {
             int id;
             for(;y>=;y--)
             {
                 int nw=mymin(x+y,pre[i][x]+num[i][j]+suf[j][y]);
                 if(f[i][j]<=nw)
                 {
                     f[i][j]=nw;
                     id=y;
                 }
                 else break;
             }
             y=id;
         }
         ans=mymax(ans,f[i][j]);
      }

     for(int i=;i<=p;i++)
      for(int j=p;j>=i;j--) f[i][j]=mymax(f[i][j],f[i][j+]);
     for(int i=;i<=p;i++)
      for(int j=i;j<=p;j++) f[i][j]=mymax(f[i][j],f[i-][j]);
     printf("%d\n",ans);
     for(int i=;i<=n;i++)
      printf("%d\n",f[s[i]][t[i]]);

     return ;
 }

2017-03-22 21:47:30