Codeforces Round #313 C. Gerald's Hexagon（放三角形）

C. Gerald's Hexagon

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Gerald got a very curious hexagon for his birthday. The boy found out that all the angles of the hexagon are equal to .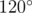
Then he measured the length of its sides, and found that each of them is equal to an integer number of centimeters. There the properties of the hexagon ended and Gerald decided to draw on it.

He painted a few lines, parallel to the sides of the hexagon. The lines split the hexagon into regular triangles with sides of 1 centimeter. Now Gerald wonders how many triangles he has got. But there were so many of them that Gerald lost the track of his counting.
Help the boy count the triangles.

Input

The first and the single line of the input contains 6 space-separated integers a1, a2, a3, a4, a5 and a6 (1 ≤ ai ≤ 1000)
— the lengths of the sides of the hexagons in centimeters in the clockwise order. It is guaranteed that the hexagon with the indicated properties and the exactly such sides exists.

Output

Print a single integer — the number of triangles with the sides of one 1 centimeter, into which the hexagon is split.

Sample test(s)

input

1 1 1 1 1 1

output

6

input

1 2 1 2 1 2

output

13

Note

This is what Gerald's hexagon looks like in the first sample:

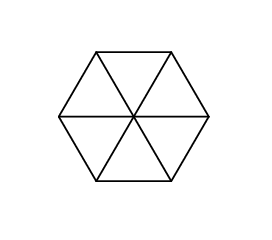
And that's what it looks like in the second sample:

    题意：给出一个每一个内角都是120度的六边形，问这个六边形中能够放多少 

个边长为1的等边三角形

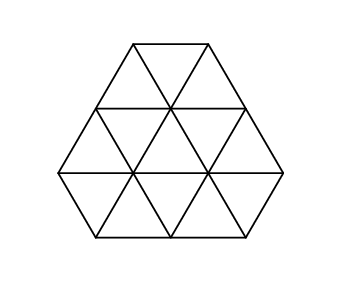
#include<iostream>
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<algorithm>
#include<math.h>

using namespace std;

int a[10];
__int64 sum;

int main()
{
    while(scanf("%d",&a[0])!=EOF)
    {
        int pt1,pt2;
        sum = 0;
        for(int i=1;i<6;i++)
        {
            scanf("%d",&a[i]);
        }
        int i,j;
        pt1 = a[0];
        i = 1;
        j = 1;
        while(i<=a[5] && j<=a[1])
        {
            sum += (pt1 * 2) + 1;
            pt1 = pt1 + 1;
            i++;
            j++;
        }
        pt2 = a[3];
        i = 1;
        j = 1;
        while(i<=a[2] && j<=a[4])
        {
            sum += (pt2 * 2) + 1;
            pt2 = pt2 + 1;
            i++;
            j++;
        }
        if(pt2<pt1)
        {
            int ps = pt1;
            pt1 = pt2;
            pt2 = ps;
        }
        int pans = abs(a[2] - a[4]) + abs(a[1] - a[5]);
        int pk = pt2 - pt1;
        while(pt1<pt2)
        {
            sum += pt1 * 2 + 1;
            pt1++;
        }
        sum += (pans - pk) * pt2;
        printf("%I64d\n",sum);
    }
    return 0;
}